Глава 4. Синтез надежных нейронных сетей

§ 4.1. О надежности функционирования формальных нейронов

В работах Вербика [32, 33], Коуэна [34, 35], Майра [36, 37] и других авторов исследуются причины и результаты неправильного функционирования формальных нейронов. Ими рассматривается упрощенная модель нейрона, хотя и опирающаяся на нейрофизиологические данные, но обедненная отказом от одного из типов синаптических связей и с малым числом входов. В терминах настоящей работы указанные авторы исследовали формальные нейроны с двумя (иногда тремя) входами и двумя типами волокон (называемых этими авторами "линиями"): возбуждающими и тормозящими. Отказ от запрещающих волокон привел к невозможности вычисления отдельным нейроном любой из 2²ⁿ функций n переменных. При n = 2 из 16 функций не вычисляются две^*: (х₁х̄₂∨ х̄₁х₂) = (6)₂ и (x₁х₂ ∨ x̄₁x̄₂) = (9)₂, а при n = 3 из 256 возможных функций нельзя вычислить 152 (этот вопрос подробно будет рассмотрен в главе 5). Для вычисления этих функций при помощи нейронов без запрещающих волокон необходимо синтезировать сети, состоящие из определенным образом соединенных между собой формальных нейронов.

^* (Иногда будем использовать запись логической функции в виде десятичного эквивалента двоичного числа, представляющего собой линейную запись идеальной диаграммы Венна. Например, x₁x₂∨x̄₁x̄₂ - (0,1,0,1) = (0101) = (5)₂. Индекс показывает число переменных.)

В [32] рассматриваются три основные причины неправильного функционирования формальных нейронов:

а) синаптический отказ, действие которого характеризуется вероятностью P_s. Проявляется в том, что формальный нейрон получает возбуждение (или торможение) от входной линии (ветви), находящейся в состоянии "выключено", либо в том, что он не получает воздействия от входной линии, находящейся во включенном состоянии. Предполагается, что вероятность одинакова для всех входных линий и не зависит от характера работы нейрона;

б) аксональный отказ, действие которого учитывается вероятностью Р_а. Аксональный отказ состоит в том, что выходная линия (аналог аксона) не переходит в состояние, предписанное ей функционированием формального нейрона. Как синаптический, так и аксональный отказ носят дискретный характер и в этом смысле относятся к отказам типа "все или ничего";

в) флуктуация порогового значения 0, следствием которой является вероятность отказа P_t. Флуктуация порога имеет длительный характер и приводит к изменению вычисляемой нейроном функции.

Полагая пороговые флуктуации независимыми от аксональных отказов, можно учесть их совместное воздействие на нейрон при помощи вероятности Р_α:

Кроме трех рассматриваемых причин ошибок в функционировании формальных нейронов, четвертым фактором, влияющим на их надежность, является флуктуация амплитуды сигналов, получаемых нейронами от входных линий (волокон). Однако дискретный характер работы нейронов обусловливает небольшое значение флуктуаций сигналов как в биологических нейронах, так и в технических реализациях формальных нейронов. Кроме того, влияние флуктуации интенсивности входных сигналов уменьшается с ростом числа входных линий (волокон). Все эти обстоятельства позволяют пренебречь флуктуациями интенсивностей сигналов и полагать, что суммарное воздействие последних на нейрон всегда является целым числом.

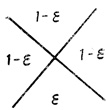
Рис. 4.1

В своей последующей работе [33] Вербик, подобно Коуэну [35], в качестве основного источника ненадежности нейронов рассматривает аксональную ошибку, вероятность которой принимается равной ε. В связи с тем, что аксональная ошибка является результатом ошибочного вычисления по истинным аргументам, в качестве основного аппарата предлагается использовать вероятностную логику, а не логику случайных аргументов. Вероятностные логические функции могут быть представлены при помощи венновской символики. Например, на рис. 4.1 показан символ, представляющий собой логический элемент, выход которого y₁ равен "1" с относительной частотой (1 - ε) всякий раз, когда на входе имеются сигналы х₁ или х₂ или оба вместе, и равен "0" с относительной частотой (1 - ε), когда на входе нет этих сигналов. Это равносильно утверждению, что при отсутствии сигналов х₁ и х₂ на выходе y₁ имеется "1" с относительной частотой ε.

Очевидно, что этот символ может быть интерпретирован как функция х₁ ∨ x₂ = (7)₂ такая, что каждому возможному соотношению входа и выхода соответствует определенная вероятность ошибки ε.

Важна заметить, что через аксональную ошибку формального нейрона можно выразить и любые ошибки, появляющиеся в результате флуктуации порогового значения нейрона.

В частности, катастрофические отказы нейронов можно представить через скачок порогового значения либо до + ∞ (когда нейрон не дает выходного сигнала при любых входных воздействиях; в терминах работы [33] - death^*), либо до - ∞ (когда нейрон выдает выходной сигнал при любых входных воздействиях; в терминах работы [33]-fit^**). По-видимому, любые другие ошибки аксонального выхода нейронов могут быть выражены через соответствующие промежуточные скачкообразные изменения порогов.

^* (Смерть.)

^** (Припадок, пароксизм.)