§ 4.2. О надежности функционирования простейших сетей из формальных нейронов

Из формальных нейронов синтезируют нейронные сети, имея в виду двоякую цель: а) реализовать при помощи сети те функции, которые не могут быть осуществлены на одном нейроне;

б) повысить надежность вычисления логических функций. Первая из этих двух задач актуальна для синтеза сетей из формальных нейронов, не имеющих запрещающих волокон (см., например рис. 4.2, на котором показана сеть, реализующая функцию х₁х₂ ∨ x̄₁х̄₂ = (9)₂, которую нельзя осуществить на одном двух входовом нейроне, не имеющем запрещающих волокон), вторая задача актуальна для синтеза сетей из формальных нейронов любого типа.

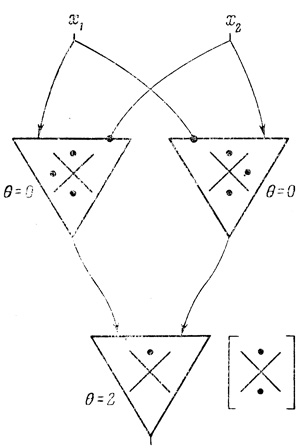
Рис 4.2

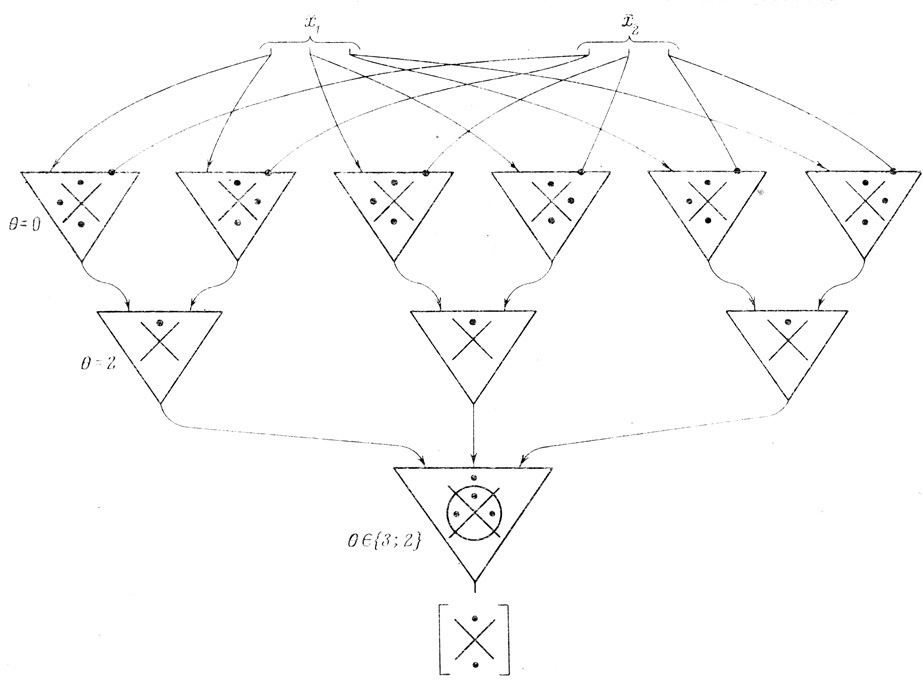
Рис 4.3

При рассмотрении надежности работы сетей формальных нейронов делаются два упрощающих допущения:

1. Предполагается, что все нейроны в сети имеют одно и то же значение вероятности ошибки ε; если ожидаются различия в значениях вероятности ошибок для различных нейронов, то выбирается наибольшее из них, которое и принимается за значение ε для всех нейронов сети.

2. Предполагается, что вероятность ошибки не зависит от предыдущего или настоящего состояний (входных последовательностей) как данного нейрона, так и любых других нейронов сети.

Ошибки каждого из формальных нейронов сети (по допущению одинаковые и равные ε) обусловливают некоторую результирующую ошибку сети, равную η. Вполне очевидно, что вероятность ошибки сети должна превосходить вероятность ошибки выходного нейрона, т. е. η>ε. Вначале предлагается метод снижения величины η до значения η'<η, соизмеримого с ε. Для этого вычисляют требуемую функцию m раз, после чего выходные линии подаются на мажоритарный орган, выход которого имеет вероятность ошибки η'<η. Мажоритарный орган представляет собой формальный нейрон с т входами, который возбуждается, когда большинство из них находится в положении "включено". На рис. 4.3 показана такая схема для вычисления уже упоминавшейся функции х₁х₂ ∨ х̄₁х̄₂ = (9)₂.

В этом случае нейрон, исполняющий роль мажоритарного оргагана, вычисляет функцию y₁y₂ ∨ y₂y₃ ∨ y₃y₁ = (23)₃.

Далее рассматривается общий случай произвольного нечетного m, для которого большинство составляет (m + 1)/2 и более.

Поскольку каждой из m входных линий мажоритарного элемента присуща ошибка η, то вероятность того, что большинство из этих линий ошибочны, вычисляется при помощи биноминального распределения:

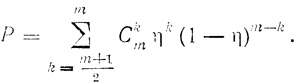(4.2)

Рис. 4.4 показывает графическую зависимость значений Р в функции от η для случаев, когда m = 1, 3, 7, 25 и 49. Для тех же значений т зависимость вероятности конечной ошибки η' = ε (1 - р) + (1 - ε) р = ε + р - 2εр при ε = 0,2 показана в функции от η на графике рис. 4.5.

Из графиков следует, что при данном ε можно достичь значений

η'<η только в том случае, если число m достаточно велико. В [33] рекомендуется m выбирать таким, чтобы выполнялось соотношение

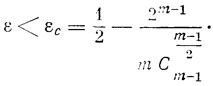(4.3)

Графическая зависимость ε_с от m показана на рис. 4.6.

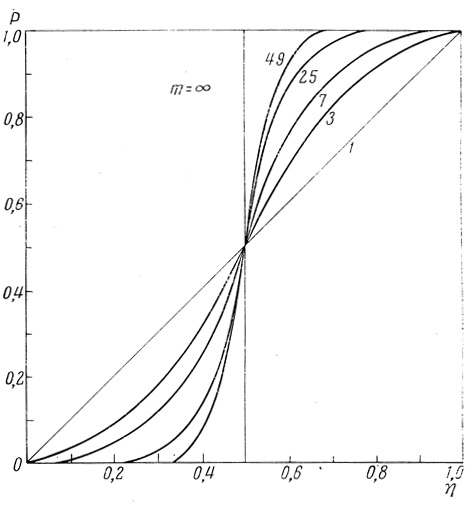
Рис. 4.4

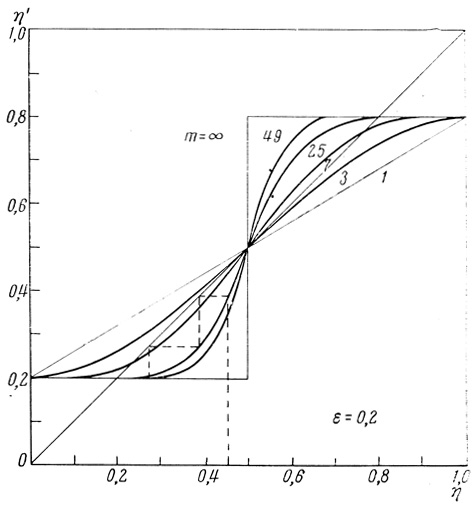
Рис. 4.5

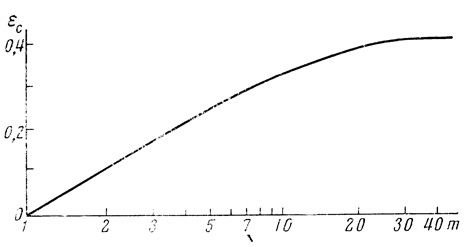
Рис. 4.6

Для фиксированных значений m и ε<ε_c дальнейшее снижение η' можно достичь за счет повторного использования мажоритарного органа, как это показано для случая m = 3 на рис. 4.7.

Пунктирная линия на рис. 4.5, иллюстрирующая результат повторного использования мажоритарного органа, показывает, что значение конечной вероятности ошибки η' при росте числа таких повторений быстро уменьшается, приближаясь к значению ε.

В том случае, когда требуемая функция вычисляется одним формальным нейроном, необходимость в сети для обеспечения ошибки ≈ε вообще отпадает.

Это обстоятельство является одним из серьезных доводов за использование формальных нейронов, имеющих запрещающие волокна, что позволяет каждому из них реализовывать любую из всех возможных 2²ⁿ логических функций. Так, например, уже упоминавшаяся функция (9)2, показанная на рис. 4.2, для реализации которой из нейронов без запрещающих волокон требовалась специальная сеть, реализуется одним формальным нейроном с запрещающими волокнами (рис. 4.8).

При использовании нейронов без запретов понадобилось бы создать сеть типа показанной на рис. 4.3, но для достижения той же вероятности ошибки, которую имеет один нейрон (ε), пришлось бы принять m = 5, на что понадобилось бы 16 формальных нейронов.

Рис. 4.7

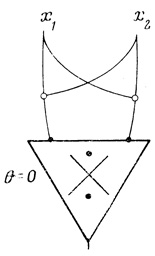
Рис. 4.8

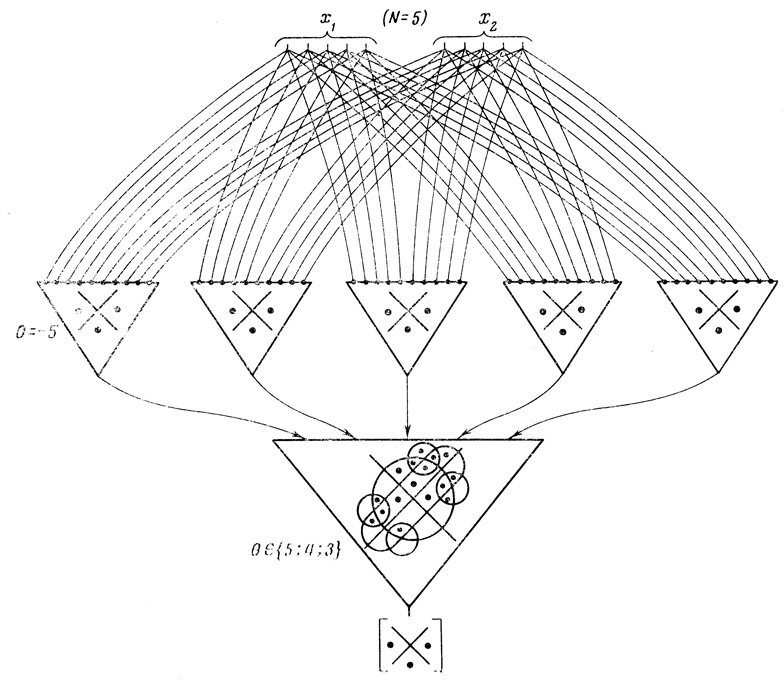
Рис. 4.9

Изложенный метод был разработан Вербиком в развитие идей Неймана [14] с целью построения сетей, имеющих тот же уровень вероятности общей ошибки, что и у Неймана, но при существенно меньшем количестве необходимых элементов. Этого удалось достичь за счет отказа от мажоритарного элемента с тремя входными линиями (как у Неймана) и использования элемента с т входными линиями, в котором влияние неисправной линии оказывается ниже. Развивая далее эти идеи и стремясь снизить вероятность конечной ошибки сети к величине, находящейся ниже вероятности ошибки выходного нейрона 8, Вербик, следуя Нейману, предложил применить пучкование и принцип "все со всеми" (all-to-all). В соответствии с этим принципом каждая переменная подается по пучку из N линий к каждому из N формальных нейронов, выходы которых поступают на мажоритарный элемент (например, как показано на рис. 4.9, для реализации функции х̄₁ ∨ х̄₂ = (7)₂ при N = 5). При фидуциальном^* уровне Δ (0 < Δ < 0,5) утверждается, что переменная соответствует единице, если (1 - Δ) N или более линий пучка находится в состоянии "включено", и переменная соответствует нулю, если в состоянии "включено" находится ΔN или менее линий пучка. В промежуточном состоянии, когда число возбужденных линий находится между (1 - Δ) N и ΔN, переменная не несет информации, и это состояние интерпретируется как "неисправность". Передача входной информации по многим линиям пучка к каждому из решающих элементов позволяет наиболее эффективно использовать возможности, которые может дать избыточность для снижения общей вероятности ошибки сети до уровня ниже ε.

^* (fiducial - принятый за основу сравнения.)

В качестве примера рассмотрим случай вычисления функции х₁х₂ = (1)₂ при помощи сети с N = 10 (т. е. в каждом из пучков х₁ и х₂ имеется по 10 линий, подаваемых на каждый из десяти решающих нейронов). Так как максимальное число ошибочных линий не должно превышать ΔN, то из условия 10 + ΔN < θ ≤ 20 - 2ΔN следует, что необходимо принять фидуциальный уровень Δ<1/3. Если ΔN = 3, то θ = 13,5 ± 0,5. Увеличение допуска, на изменение порога, естественно, влечет за собой требование к уменьшению уровня А. В данном случае сеть будет свободной от ошибок, если не более трех линий в каждом из пучков будет ошибочных.

Если теперь считать, как и прежде, ошибки в формальных нейронах независимыми и равными ε, то вероятность Ре того, что более чем ΔN линий выходного пучка ошибочны, т. е. вероятность общей ошибки, можно вычислить из соотношения

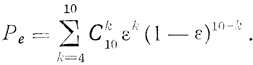
Для случая, когда ε = 0,005, Р_е ≈ 1,3×10^-7. Таким образом, пучкование в сочетании с принципом "все со всеми" делает схему нечувствительной к относительно большому числу ошибочно работающих линий в пучках (Δ<1/3 вместо Δ = 0,07 по схеме Неймана).

Естественно, что увеличение числа волокон, поступающих на формальный нейрон, в общем случае уменьшает эффект синаптических ошибок. Это дает возможность получить вероятность ошибки Ре сети по величине существенно более низкую, нежели вероятность погрешности ε отдельного нейрона.

Вербик одновременно показал [33], что при использовании 15 000 двухвходовых нейронов с погрешностью ε = 0,005 в сети Неймана получается вероятность ошибки Р_е ≈ 4×10^-6.

В другой работе [32] Л. Вербик, не приводя выкладок, утверждает, что, используя нейроны в 10 раз менее надежные, чем у Неймана, он указанными методами может получить ту же надежность при наличии в пучке в 200 раз меньшего числа линий. Все это делает достоинства пучкования, использования принципа "все со всеми" и многовходовых мажоритарных элементов особенно наглядным. В той же работе [32] доказывается общее утверждение: все логические функции n переменных (передаваемых пучками по N линий для каждой переменной), представленных диаграммами Венна с одной точкой (и 2ⁿ-1 нулями) или одним нулем ( 2ⁿ-1 точками), могут быть, вычислены рядом из N нейронов безошибочно в том случае, если количество неисправно работающих линий в пучке удовлетворяют неравенству

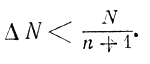(4.4)

Пусть ячейка, содержащая точку, соответствует пересечению и переменных. Тогда и возбуждающих и (n - u) тормозящих пучков подаются на нейрон, причем максимальное количество ошибочных линий на пучок будет ДМ. Тогда вычисление будет безошибочным^ если порог нейронов выбран из условия

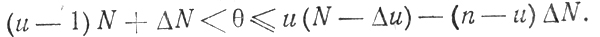
Отсюда следует, что ΔN N/(n + 1).

Доказательство для функций, представленных в диаграммах одним нулем и(2ⁿ - 1) единиц, аналогично.

Так как среди 2²ⁿ функций n переменных имеется

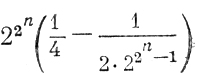
полифеков^* [16], то располагая достаточным числом n входовых формальных нейронов, всегда можно по изложенной методике построить сеть для вычисления любой произвольно заданной логической функции с заданным уровнем надежности ее реализации.

Пучкование входных линий и принцип "все со всеми" детально рассмотрены Коуэном [35] с точки зрения использования математического аппарата многозначных логик. В частности, им показано, что функционально неполная логика Лукасевича и функционально полная логика Поста дают возможность моделировать более эффективные избыточные надежные сети. Основные выводы Коуэна сводятся к тому, что избыточный автомат может быть описан с помощью различных систем многозначных Логик, в которых не все истинные значения имеют информационный смысл, и что эти логики имеют изменяющуюся структуру, которая соответствует различным методам кодирования и обработки информации; поиск путей достижения надежных вычислений на ненулевых скоростях при наличии шума облегчается использованием этих логик [34, 35].

^* (О полифеках см. в § 4.4)