§ 4.3. Синтез надежных нейронных схем при помощи карт стабильности
Майтра в своей докторской диссертации (основные результаты которой изложены в работах [36] и [37]) предложил использовать так называемые карты стабильности для анализа и синтеза элементарных надежных схем, состоящих из трех двухвходовых нейронов, образующих триплет. Автор поставил своей целью получить решение задачи, отличающееся от решения как Неймана [14], так и Мура-Шеннона [38] тем, что она не зависит от конечной допустимой надежности выходного элемента и не использует избыточности на уровне ниже, чем функциональные модули - нейроны. В рамках формального нейрона Мак-Каллока предполагается, что элемент может находиться в различных функциональных состояниях из некоторого ограниченного множества их, причем то состояние, в котором находится нейрон в данный момент времени, определяется пороговым числом.
Необходимо так синтезировать схему, чтобы поведение ее (т. е. соотношения вход - выход для каждого момента времени) оставалось неизменным при изменениях функциональных состояний нейронов. Эти изменения являются следствием воздействий внешней среды, проявляющихся через изменения порогов.
Как и Нейман, Майтра считает устойчивость нейронных цепей (в указанном смысле) источником надежности поведения человека в неблагоприятных условиях существования.
За функциональный модуль был принят триплет. Поведение функционального модуля может описываться вероятностным вектором P1,....,Pk), соответствующим вектору логической функции (f1,....., fk). Наибольшей составляющей вектора вероятностей должна быть Pj, если модуль предназначен для реализации функции fj. Из простых триплетов могут составляться более сложные, или триплеты более высоких порядков.
Для анализа и синтеза простых и сложных триплетов используются вероятностная логика и так называемые карты устойчивости.
Рассмотрим триплет, показанный на рис. 4.10. Он состоит из трех двухвходовых нейронов, каждый из которых, в свою очередь, может состоять из любых физических элементов. Наличие в символах нейронов (треугольниках) вместо диаграмм Венна букв F1, F2, F3 указывает на то, что функции этих нейронов должны быть найдены из общего числа 22n = 222 = 16 независимых функциональных состояний, но только таких, чтобы было обеспечено выполнение заданной функции F. Выходы ячеек F1 и F2 обозначаются соответственно через α и β.
Таблица устойчивости триплета показана на рис. 4.11. Входные последовательности входов а и b составляют строчки таблицы; комбинации выходов аир ячеек F1 и F2 размещаются в столбцах таблицы. Таблица содержит 232 = 161 (при n = 2) элементов аij.
В крайнем правом столбце таблицы представлена заданная функция F, а в последней строке таблицы записывается функция выходного элемента F3. Для последовательности, которой в диаграмме соответствует точка, здесь записывается единица, а вместо "пустышки" (пустой ячейки) - нуль.
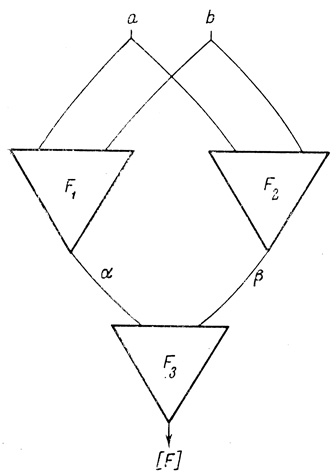
Рис. 4.10
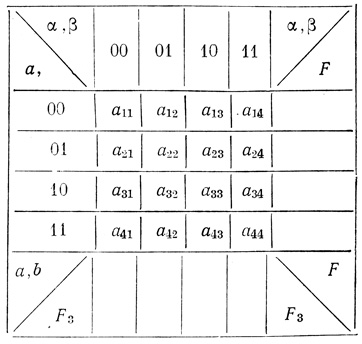
Рис. 4.11
Построение карты стабильности рассмотрим на конкретном примере.
Требуется получить F = ab ∨ āb̄, причем F3 может вычислять одну из двух функций: F31 = α∨β или F32 = α∨β. Для каждой из функций, которые может вычислять F3, необходимо составить свою карту стабильности (рис. 4.12 и 4.14).
Поскольку функции F и F3 описывают один и тот же выход, они логически эквивалентны. Отсюда следует, что при F = 1 должно быть и F3 = 1, а также при F = 0, F3 = 0. Это требование приводит к тому, что комбинация αβ, соответствующая элементу aij карты, находящемуся на пересечении взаимно противоречащей пары значений F и F3 (0 и 1,1 и 0), не может быть подана на вход нейрона F3. Ячейки, содержащие такие аij, заштриховываются. Если теперь в качестве комбинации функциональных состояний ячеек F1 и F2 выбирать любые комбинации из не заштрихованных элементов, работа такого триплета будет устойчивой.
Из не заштрихованных элементов карты стабильности необходимо выбрать по одному элементу в каждой из строк. Если все элементы хотя бы одной из строк оказываются заштрихованными, то не существует функциональных представлений F1 и F2, в сочетании с F3 дающих заданную функцию F.
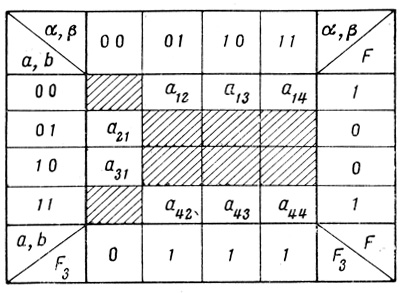
Рис. 4.12
В рассматриваемом примере (рис. 4.13) при F3 = α∨β имеется 32 = 9 наборов аij, обеспечивающих построение триплета
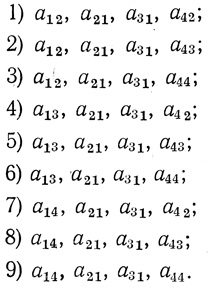
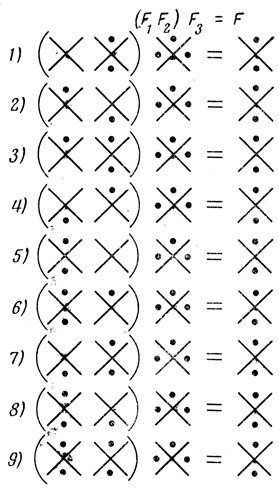
Рис. 4.13
Рассмотрим подробно один из них, например, 2) a12, а21, а31, а43.
Таблица истинности функций α (а, b) и β (а, b), соответствующая этому случаю, имеет вид:

Это значит, что в ячейке 0 (а̄∨b̄) у F1 должна быть пустышка (α = 0), а у F2 должна быть точка (β = 1); в ячейках 1 (а̄ & b) и 2 (а & b̄) в F1 и в F2 должны быть пустышки (α = β = 0); наконец, в ячейке 3 (а & b) в F1 должна быть точка (α = 1), а в F2 - пустышка (β = 0).
Таким образом, получается сеть, показанная на рис. 4.2. Значения α и β для всех вариантов сведены в табл. 4.1.
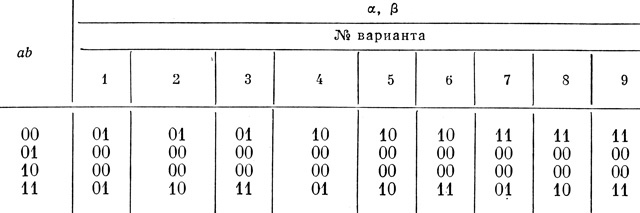
Таблица 4.1
Для краткости записи все 9 возможных вариантов построения сети показаны на рис. 4.13 в виде (F1, F2) F3 = F. Легко убедиться, что все приведенные на этом рисунке сети осуществляют требуемую функцию F = ab ∨ āb̄.
Теперь построим карту стабильности для случая, когда ячейка F3 принимает значение F3 = а & b (рис. 4.14). В этом случае может иметь место также 9 наборов aij удовлетворяющих требуемым условиям:
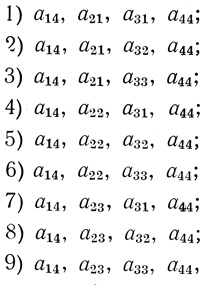
Как и в предыдущем случае, составим вспомогательную таблицу значений α, β для каждого из девяти вариантов допустимых наборов aij (табл. 4.2).
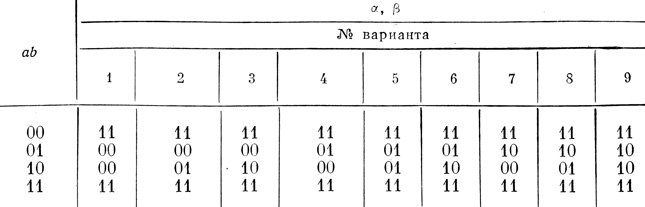
Таблица 4.2
По данным табл. 4.2 легко строятся и все девять сетей, показанных на рис. 4.15. Здесь, так же как и в предыдущем случае, показаны все допустимые комбинации функциональных состояний F1 и F2 приводящих к получению устойчивой цепи, реализующей заданную функцию при данной ячейке Fs. Никаких других решений этой задачи, помимо найденных девяти, нет.
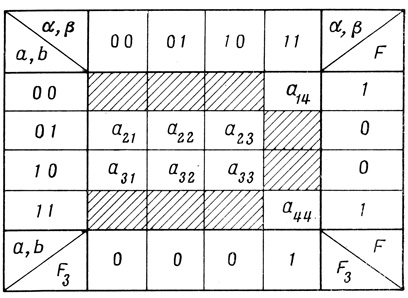
Рис. 4.14
В связи с тем, что логический модуль может быть описан вектором вероятностей, поведение триплета в целом также может быть описано вектором вероятностей, для построения которого используем так называемую карту (или матрицу) надежности. Вероятностная функция, соответствующая той логической функции, которую желательно реализовать при помощи триплета, является функцией надежности, и поэтому вероятностную карту, из которой получается функция надежности, назвали картой (или матрицей) надежности. Построение карты надежности покажем на уже начатом примере построения триплета для реализации функции F = ab ∨ āb̄. Предварительно допустим, что ячейки F1, F2 и F3 могут быть описаны функциональными и вероятностными векторами, показанными на рис. 4.16.
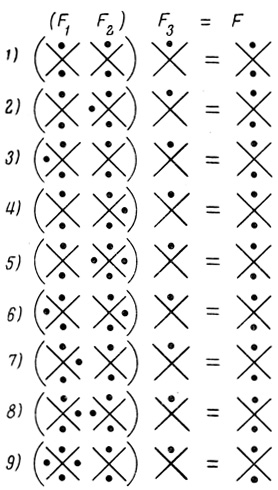
Рис. 4.15
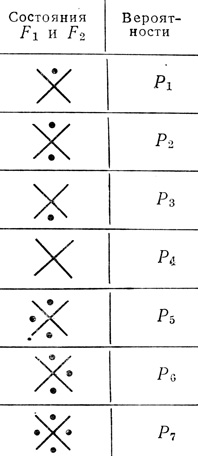
Рис. 4.16
Для построения карты надежности необходимо предварительно построить для заданных F и всех возможных состояний F3 карты стабильности. Для нашего примера такие карты уже построены (рис. 4.12 и 4.14). Карты надежности строятся для каждого функционального состояния F3 в отдельности. В данном случае необходимо построить две карты надежности (рис. 4.17 и 4.18). Карта надежности рис. 4.17 построена для фуцкционального состояния F3 = а ∨ b в соответствии с картой стабильности рис. 4.12. Очевидно, существует 16 комбинаций функциональных состояний F1 и F2, представленных в картах для F31 и F32, в которых четыре строки и четыре столбца обозначены четырьмя возможными состояниями F1 и F2 соответственно. Элемент карты Rij содержит условную вероятность Pi×Pj совместного появления состояний Fi и F2j при условии, что Pi×Pj независимы. Запись всех возможных Pi×Pj составляет первый этап построения карты надежности, который не зависит от количества и вида функциональных состояний ячейки F3.
Теперь необходимо выбрать такие условия вероятности Pi×Pj, которые соответствуют комбинациям состояний F1 и F3, приводящим к реализации триплетом желаемой функции F = ab ∨ āb̄. В карте надежности таким элементам Rij приписывается коэффициент 1, элементам Rij, не приводящим к вычислению требуемой функции Fr приписывается коэффициент 0.
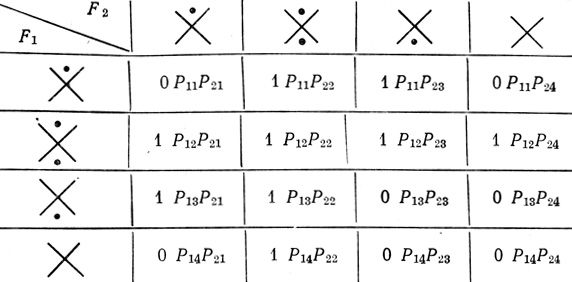
Рис. 4.17
Практически удобно при помощи карт стабильности определить те Rij, которые должны иметь коэффициент 0, а оставшимся Rij можно приписать 1. Рассмотрим подробно методику расстановки коэффициентов для нашего примера при F3 = а ∨ b.
Рассматриваем последовательно каждую из заштрихованных ячеек карты стабильности (рис. 4.12).
1. Штриховка элемента а11 означает, что не допускается одно-временное отсутствие точек в ячейках (0)2 = а & b (а = 0; b = 0) символов и F2 (α = 0, β = 0); поэтому в карте надежности ставим нули в тех ячейках, где это условие не выполняется, т. е. в ячейках R11, R14, R41, R44.
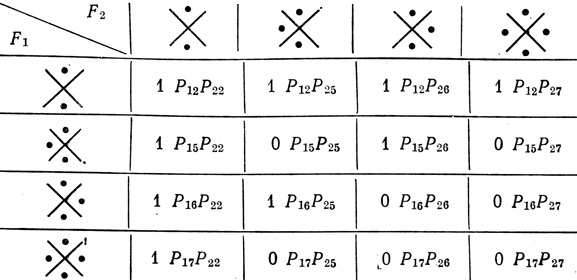
Рис. 4.18
2. Штриховка элемента а22 означает, что в ячейках (4)2 = а̄ & b (а = 0; b = 1) не допускается отсутствие точки у F1 (а = 0) и одновременное наличие ее у F2 (β = 1); однако среди допустимых функциональных состояний F1 и F2 отсутствуют такие, которые содержат точки в ячейках а̄ & b, поэтому штриховка элемента а22 никакой информации для составления карты надежности не дает. То же можно сказать и о штрихованных элементах а23, a24, a32, a33, a34.
3. Штриховка элемента а41 карты стабильности означает, что не допускается в ячейках (1)2 = a&b (а = 1, b = 1) символов F1 и F2 одновременное отсутствие точек (α = 0, β = 0); поэтому в карте надежности ставим нули в тех ячейках, где это условие не выполняется, т. е. в ячейках R33, R34, R43 (это условие не выполняется и в ячейке i?44, но коэффициент 0 был поставлен в этой ячейке раньше).
Все заштрихованные ячейки карты стабильности исчерпаны, поэтому в девяти ячейках карты надежности, в которых не были выставлены нули, ставим единицы. Элементы Rij этих ячеек применимы для реализации триплетом желаемой операции F и поэтому имеют коэффициенты 1. На этом заканчивается составление карты надежности для состояния F3 = а ∨ b.
Аналогичным образом составляются карты надежности и для всех остальных возможных функциональных состояний F3 (в данном случае - для состояния F3 = а & b, карта надежности которого показана на рис. 4.18).
Теперь функция надежности H (Rij) получится как сумма условных вероятностей всех комбинаций состояний F1, F2, F3, которые приводят к получению желаемой операции F = ab ∨ āb̄. Эту сумму Майтра назвал надежностью.
Каждая карта надежности дает вероятность выполнения требуемой логической операции при условии, что имеет одно функциональное состояние; эту вероятность, полученную суммированием тех элементов карты надежности, которые имеют коэффициент 1, и обозначаем через Hi.
В нашем примере
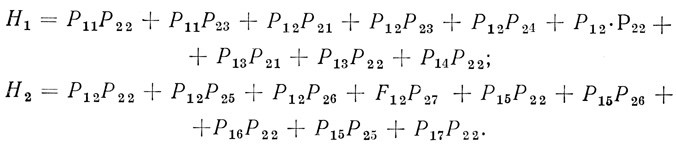
Общая функция надежности триплета в данном случае будет получена из формулы
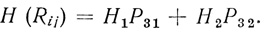
Если положить, что элементы, идущие для F1 и F2, имеют одинаковые вероятности функционированных состояний, т. е. что
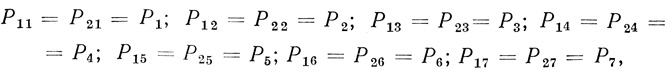
то вероятность выполнения триплетом заданной функции будет
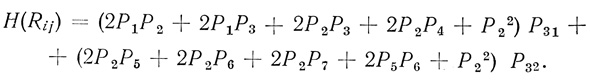
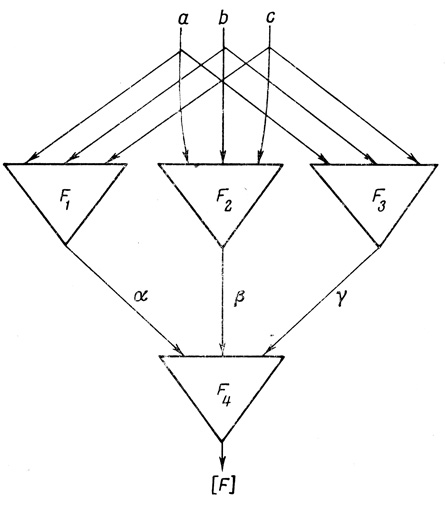
Рис. 4.19
Для уменьшения числа таблиц можно составить одну карту надежности для всех функциональных состояний F3. В ячейках этой карты будет находиться (в виде столбика) столько коэффициентов 1 и 0, сколько состояний может принимать элемент F3. При вычислении общей функции надежности триплета коэффициенты каждого элемента карты умножаются на вероятности P3j соответствующих состояний выходного нейрона F3. Такие карты надежности будут использованы в дальнейшем изложении материала.
В работах [36] и [37] Майтра рассматривал сети, состоящие только из двух двухвходовых нейронов в первом ранге и одного во втором,- так называемые триплеты. Однако тот же метод можно распространить на более сложные сети, например на трехвходовые двухранговые сети, состоящие из четырех формальных нейронов, которые назовем квадруплетами (рис. 4.19). В связи с тем, что в ряде работ ([13, 39]) показана необходимость использования по крайней мере трехвходовых нейронов, такое обобщение представляется весьма целесообразным.
Рассмотрим построение карт стабильности и надежности для квадруплетов на примере вычисления функции F = а & b & с. Теперь необходимо рассмотреть те комбинации F1, F2 и F3 которые в сочетании со всеми возможными функциональными состояниями F4 дадут заданное F, т. е. (F1, F2, F3) F4 = F.
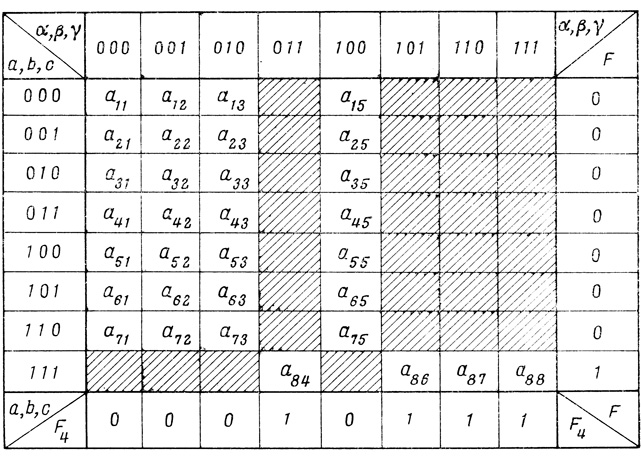
Рис. 4.20
Для простоты примем непринципиальное для сути дела предположение о том, что F4 имеет только одно функциональное состояние
F4 = (23)3 = (0, 0, 0, 1, 0, 1, 1, 1) = abc ∨ abc̄ ∨ ab̄c ∨ ābc.
Построение карты стабильности квадруплета (рис. 4.20) не вызывает никаких трудностей и производится по тем же правилам, что и для триплетов.
Отметим, что число возможных наборов аij, допускающих построение цепи, реализующей заданную функцию, резко возрастает (по сравнению с соответствующей величиной при синтезе триплетов). Из рис. 4.20 следует, что в данном случае может быть 48 = 65 536 таких наборов*.
* (Если li - число не заштрихованных ячеек i-й строки карты стабильности то общее число допустимых наборов аij, реализующих заданную функцию F, будет N=Πi li.)
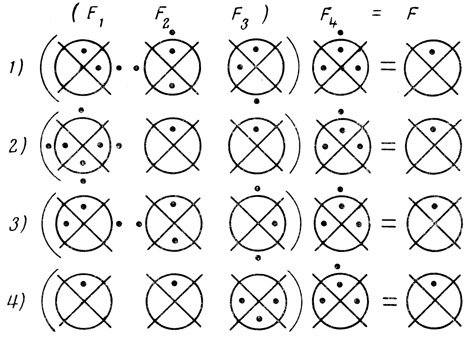
Рис. 4.21
Исходя из понятия логической избыточности, можно утверждать что такое обилие комбинаций различных функциональных состояний нейронов F1, F2, F3 является источником надежности сети.
Не имея необходимости рассматривать все 65 536 возможных комбинаций aij, убедимся в правильности работы квадруплета, построенного по четырем случайно выбранным допустимом наборам aij:
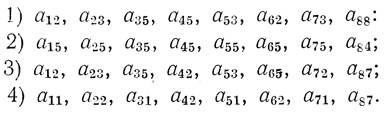
Соответствующие этим наборам сети в виде (F1, F2, F3) F4 = F показаны на рис. 4.21.
Для построения карты надежности примем вероятности функциональных состояний ячеек Fi в соответствии с рис. 4.22.
Построение карты надежности квадруплета осложняется тем, что она должна быть трехмерной. Так как возможные функциональные состояния элементов F1, F2 и F3 одинаковы, то в каждой ячейке карты надежности (рис. 4.23) необходимо разместить столько произведений Rij = PiPjPk, сколько допускается функциональных состояний для Fi (в данном случае - 5).
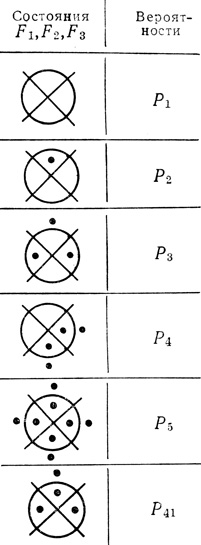
Рис. 4.22
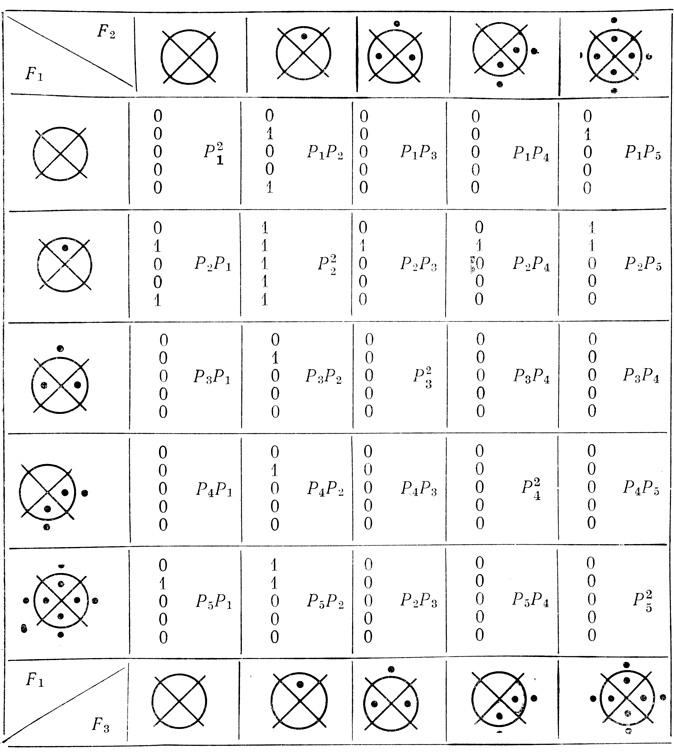
Рис. 4.23
Расстановка коэффициентов 0 и 1 производится по тем же правилам, что и для триплетов.
Из рис. 4.23 следует, что общая функция надежности квадруплета в данном случае будет получена из формулы
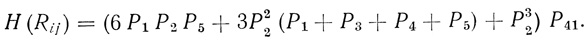
Если выходной нейрон F4 имеет несколько функциональных состояний, определяемых вероятностями Р4j, то для каждого из них необходимо составить свою карту надежности и общую функцию надежности найти как сумму
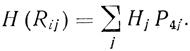
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'