§ 4.4. Преобразования и полифеки
Полифеками называются универсальные функции, любой из которых достаточно для построения исчисления высказываний*. Сети, использующие конечное число только одной из этих функций, в состоянии воспроизвести любую функцию исчисления высказываний. Одним из полифеков, в частности, является штрих Шеффера.
* (Термин "полифек" (polyphek) введен Блюмом [16].)
Чтобы определить, является ли функция n переменных, заданная точечной диаграммой Dτ, полифеком, необходимо использовать введенное в работе [16] понятие преобразований. Преобразования могут изменять логические функции, вычисляемые нейронной сетью, или функции входящих в сеть формальных нейронов, но только так, чтобы не изменить надежность сети.
Иначе говоря, если над сетью, надежно вычисляющей заданную функцию, при некотором определенном интервале изменений порогов (или порядковых чисел) производится преобразование, то последнее приводит к построению другой сети, надежно работающей на том же самом интервале.
В связи с тем, что любую логическую функцию можно представить, используя только конъюнкцию или дизъюнкцию и отрицание, функцию запишем в виде Φ (X,  Y, ∨,&)9 где X является логической переменной, вход которой возбужден, а
Y, ∨,&)9 где X является логической переменной, вход которой возбужден, а  Y - логической переменной, вход которой не возбужден. Тогда, например, если
Y - логической переменной, вход которой не возбужден. Тогда, например, если
Ф(Х,  Y, ∨, &) = (a1&
Y, ∨, &) = (a1& a2&a3)∨(
a2&a3)∨( a1&a2&a3)
a1&a2&a3)
 Y, ∨, &) = (a1&
Y, ∨, &) = (a1& a2&a3)∨(
a2&a3)∨( a1&a2&a3)
a1&a2&a3)то
Φ (X, Y, &, &) = (а1 & а2 & а3) & (а1 & а2 & а3) = а1 & а2 & а3,
что в терминах диаграмм Венна показано на рис. 4.24.
В [16] рассматривается три вида преобразований: дополнение (complement) С, двойственность (dual) D и перестановка (permutation) Р. Суть этих преобразований сводится к следующему:
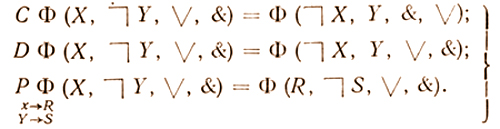 (4.5)
(4.5)
Рис. 4.24
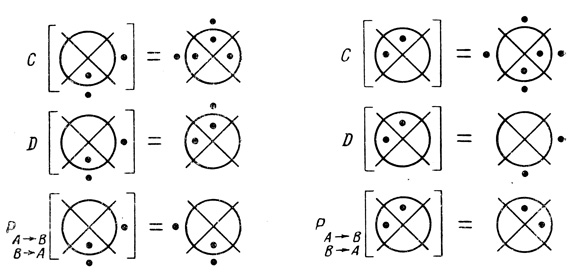
Рис. 4.25
На рис. 4.25 в терминах диаграмм показаны два примера применения преобразований С, D и Р. Из (4.5) следует, что
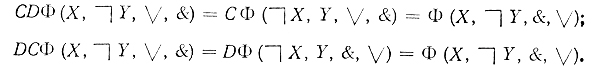
Отсюда видно, что
CDΦ = DСΦ. (4.6)
Аналогично
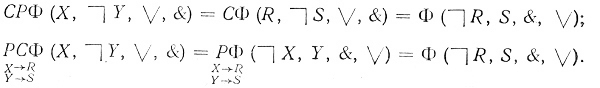
Отсюда
СРΦ = РСΦ. (4.7)
Так как
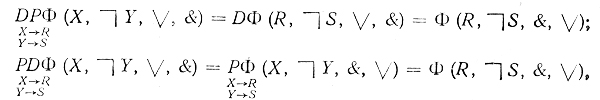
то
ОРΦ = PDΦ. (4.8)
Так как
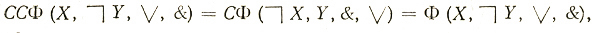
то
ССΦ = Φ. (4.9)
Так как
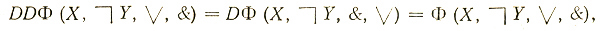
то
DDΦ = Φ. (4.10)
Наконец, так как
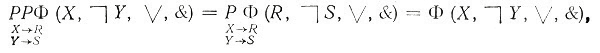
то
РРΦ = Φ. (4.11)
Применим операцию преобразований к нейронным сетям, обозначаемым, как это принято в настоящей работе, в виде
(Dτ1,i)Dτ2,i, = [Φ], (4.12)
где Φ - результирующая функция, вычисляемая сетью.
Под записью CDτr,i, DDτr,i, PDτr,i будем понимать применение данного вида преобразования ко всем диаграммам данного ранга. Тогда можно показать, что
(DDτr,i) CDDτ2,i = [СΦ]; (4.13)
(DDτr,i)Dτ2,i = [ОΦ]; (4.14)
(CDτr,i)DDτ2,i = [Φ]; (4.15)
(PDr,i)Dτ2,i = [РΦ]. (4.16)
Комбинируя между собой уравнения (4.13)- (4.16), можно получить ряд новых соотношений. Так, например, уравнения (4.13) и (4.14) дают
(DDτr,i)CDτ2,i = [DCΦ], (4.17)
а (4.17) и (4.15)
(DCDτr,i)DCDτ2,i = [DCΦ] . (4.18)
Последнее соотношение весьма важно для анализа и синтеза логически стабильных сетей (§ 4.5); оно позволяет одни логически стабильные сети преобразовать в другие логически стабильные сети. Покажем это на конкретном примере. На рис. 4.30 приведена логически стабильная сеть, вычисляющая функцию Φ = а1 а̄2 ∨ a1a2 при трех последовательных значениях порогов у нейронов. Применим ко всем диаграммам нейронов этой сети преобразования DC. Эти преобразования показаны в терминах точечных и порядковых диаграмм на рис. 4.26.
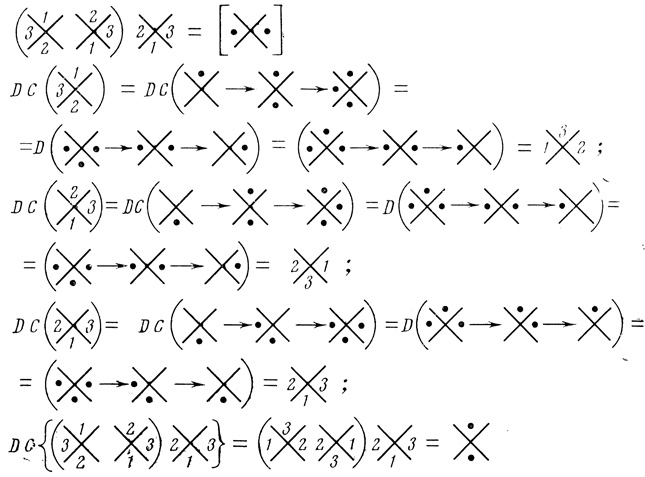
Рис. 4.26
Полученная в результате преобразований функция Φ1 = а1а2 ∨ ā1а̄2 является, во-первых, логически стабильной при трех значениях порогов и получена из функции Φ путем применения к последней преобразований DC, т. е.
Φ1 = DСΦ
В связи с тем, что отрицания и дизъюнкции или конъюнкции при заданных логических переменных достаточно для реализации исчисления высказываний, функции, которые могут дополнять и содержат конъюнкцию или дизъюнкцию, также достаточны для построения исчисления высказываний.
В работе [16] дано необходимое и достаточное условие обладания функцией свойством дополнения: для того чтобы точечная диаграмма Dτ логических переменных a ,..., аn могла дополнять функцию Φ, необходимой достаточно, чтобы в нулевой ячейке имелась точка и чтобы в ячейке 2n - 1 ее не было.
В той же работе на основе использования понятий преобразований и условия, при котором функция обладает свойством дополнения, доказана теорема, позволяющая однозначно установить, является ли данная функция полифеком.
Любая функция Φ, которая может дополнять и которая удовлетворяет условию Φ ≠ CDΦ, является полифеком. Иначе говоря, логическая функция Φ есть полифек тогда и только тогда, когда
1) ее точечная диаграмма Dτ содержит точку в нулевой ячейке, не содержит точку в последней (т. е. 2n - 1) ячейке и
2) удовлетворяется условие Φ ≠ CDΦ.
При двух переменных первому условию теоремы из общего числа 222 = 16 функций удовлетворяют четыре функции:  a1,
a1,  a2, ā1ā2, ā1∨ā2 ибо у остальных двенадцати функций либо отсутствует точка в нулевой ячейке, либо имеется точка в ячейке 2n - однако второму условию теоремы из четырех рассмотренных функций удовлетворяют только две последние (рис. 4.27). Эти две функции являются штрихом Шеффера и стрелкой Пирса.
a2, ā1ā2, ā1∨ā2 ибо у остальных двенадцати функций либо отсутствует точка в нулевой ячейке, либо имеется точка в ячейке 2n - однако второму условию теоремы из четырех рассмотренных функций удовлетворяют только две последние (рис. 4.27). Эти две функции являются штрихом Шеффера и стрелкой Пирса.
Общее число полифеков N для функции n переменных определяется из формулы
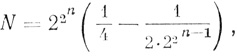 (4.19)
(4.19)так что уже трехвходовые нейроны могут образовывать 56 полифеков. Вероятность того, что произвольно выбранная функция n переменных является полифеком, равна
поэтому при n ≥ 4 ее можно считать приближенно равной
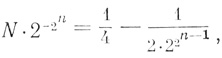
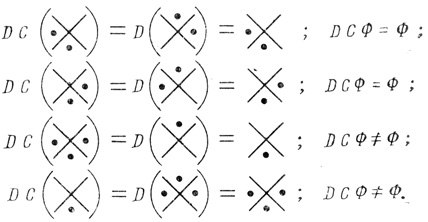
Рис. 4.27
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'