§ 4.5. Общая постановка задачи синтеза надежной нейронной сети для вычисления произвольно заданной логической функции

С точки зрения надежности формальных нейронов буква р в ячейках их вероятностных диаграмм должна интерпретироваться как вероятность наличия в данной ячейке точки. Иначе говоря, вероятностную диаграмму рис. 4.28 можно интерпретировать как предназначенную для вычисления функции Φ = а₁а₂а₃, но с вероятностью р, вычисляющей функцию Φ₁ = a₁a₂a₃∨a₁a₂ā₃.

Следовательно, вероятностная диаграмма, не содержащая букв р, выражает идеальное функционирование и поэтому не может принадлежать отдельному нейрону (так как отдельный нейрон принципиально не может быть идеально надежным), а лишь нейронной сети.

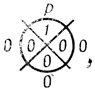
Рис. 4.28

В общем случае величины р_j, вероятностей случайного появления точки в той или иной ячейке диаграммы D^ρ могут быть различными, но для простоты будем полагать р₀ = p₁=.....= p_2ⁿ-1 = р (по- видимому, это предположение довольно близко соответствует истине, так как при технической реализации формальных нейронов количество элементов, обеспечивающих срабатывание нейрона, при той или иной входной конфигурации будет примерно одинаковым).

Таким образом, появление одной ошибочной точки в диаграмме двух переменных (n = 2) соответствует одному из четырех логически равновероятных случаев. Для диаграммы трех переменных (n = 3) ошибка будет происходить в одном из восьми логически равновероятных случаев и вообще для диаграммы n аргументов - в одном из S = 2ⁿ случаев. Если обозначить через р вероятность ошибочной отметки в диаграмме, а через Р - вероятность результирующей ошибки, то Р = 2^-nр.

Теперь для двухранговой регулярной сети из (n + 1) диаграмм (n диаграмм n аргументов в первом ранге и одна диаграмма n аргументов - оператор) снимем условия зависимости переменных. Тогда из того, что одна диаграмма n переменных может выражать F_n = = 2²ⁿ логических формул, следует, что (n + 1) диаграмм могут задавать (2²ⁿ)ⁿ⁺¹ формул. Вместе с тем из правил операций над диаграммами следует, что любая сеть может быть выражена одной результирующей диаграммой, которой соответствует только одна из 2²ⁿ формул. Отсюда вытекает уже упоминавшееся (§ 1.4) понятие логической избыточности, которая представляет собой отношение общего числа формул, задаваемых сетью, считая диаграммы независимыми, к числу формул, представляющих результат работы сети. Для двухранговой регулярной сети логическая избыточность составляет величину

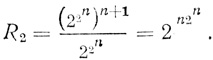(4.20)

Естественно, что если число рангов g растет, то растёт и логическая избыточность R. Так, для трехранговой сети, насчитывающей (2n + 1) диаграмм, каждая из которых может выражать 2²ⁿ формул, общее число формул, задаваемых сетью, остается прежним: F_n = 2²ⁿ. Отсюда для g = 3 имеем логическую избы-точность, равную

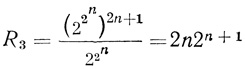(4.21)

Аналогично находим, что

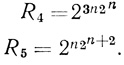(4.22)

Вообще для сети из g рангов можно написать следующую формулу:

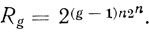(4.24)

Логическую избыточность необходимо использовать в целях повышения надежности и компенсации ошибок, вносимых отдельными диаграммами в работу сети.

Хотя работы по теории нейронных сетей носят теоретический характер, в понятие надежности функционирования в них вкладывается тот же смысл, что и в прикладной теории надежности. Например, в работе [40] надежность определяется как "...свойство аппаратуры сохранить свои выходные характеристики (параметры) в определенных пределах при данных условиях эксплуатации".

Но как раз главным свойством аппаратуры, состоящей из тех или иных физических реализаций абстрактных нейронных элементов, является нечувствительность ее к сбоям и ошибкам в отдельных элементах или даже во всех элементах одновременно. В этом смысле такая аппаратура является высоконадежной, и в связи с этим абстрактная теория формальных нейронов приобретает известный интерес для практики.

Логическая избыточность может быть использована для повышения надежности нейронных сетей двояким путем: а) построением логически стабильных сетей; б) построением логически надежных сетей.

Логически стабильной называется сеть из формальных нейронов, которая продолжает вычислять заданную логическую функцию Φ (a₁,..., a_n) при ν-кратном сдвиге (каждый раз на единицу) порогов одновременно у всех нейронов сети; пример логически стабильной сети для вычисления функции Φ (а₁, а₂) = а₁ & а₂ показан на рис. 4.29; двукратное одновременное снижение порогов у всех нейронов этой сети не искажает требуемого результата. Другой пример логически стабильной сети относительно 75%-го интервала изменения порога показан на рис. 4.30. Здесь функция Φ = а₁ а̄₂ ∨ а̄₁а₂ стабильно вычисляется при двукратном одновременном снижении порога. В последнем выражении (рис. 4.30) функционирование сети записано в терминах порядковых диаграмм, причем порядковые числа стоят только в ячейках, для соответствующих входных последовательностей которых сохраняется стабильность вычисляемой функции.

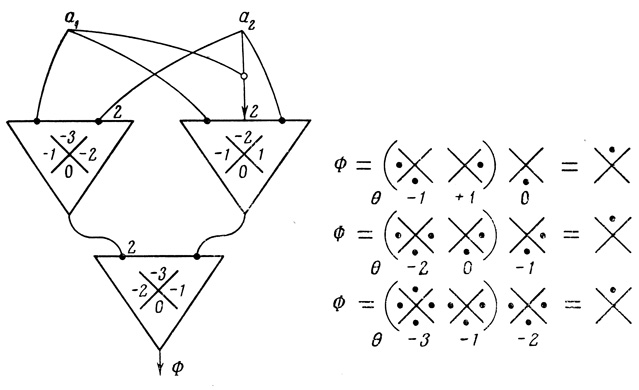
Рис. 4.29

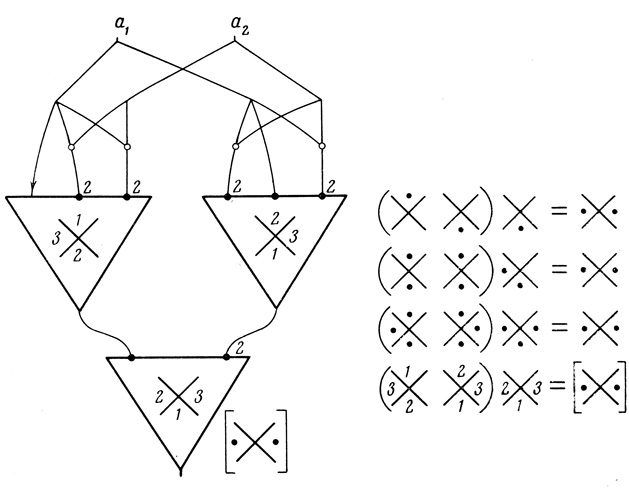
Рис. 4.30

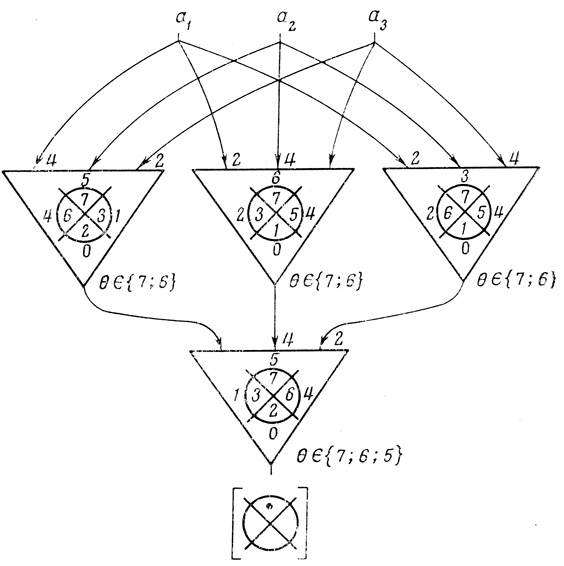
Рис. 4.31

В [16] показано, что всегда можно построить логически стабильную сеть для вычисления произвольно заданной функции с величиной интервала изменения порога нейронов равной (1- 2^-n) 102%.

Логически надежной называется сеть из формальных нейронов, которая продолжает вычислять заданную логическую функцию Φ (а₁,..., а_n) при независимых друг от друга флуктуациях функций нейронов сети; каждый из нейронов сети A_r,i (a₁,..., а_n) может независимо от других вычислять любую ошибочную функцию, определяемую некоторым множеством допустимых значений порогов Θ_r,i∈β {β₁,......,β_k} пример логически надежной сети для вычисления Φ (а₁, а₂, а₃) = а₁ & а₂ & а₃ показан на рис. 4.31; сеть вычисляет заданную функцию во всех случаях, когда пороги нейронов первого ранга независимо друг от друга принимают значения из множества Θ∈{6, 7}, а пороги выходного нейрона принимают значения из множества Θ∈ {5, 6, 7}.

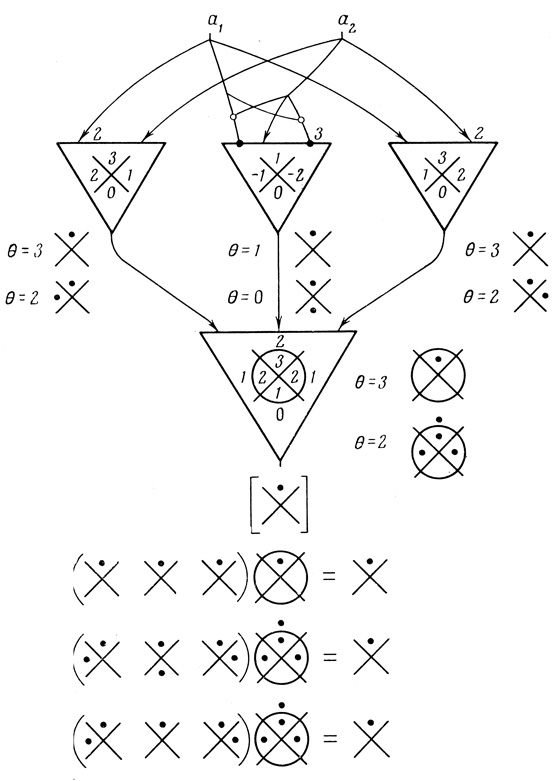
Рис. 4.32

Та же логическая функция надежно вычисляется сетью - (рис. 4.32), состоящей из трех двухвходовых нейронов в первом ранге и одним трехвходовым нейроном во втором ранге. Все нейроны этой сети могут независимо друг от друга принимать пороговые значения из множества{3;2}.

Еще один пример сети, вычисляющей функции Φ (а₁, a₂) = a₁ & a₂ показан на рис. 4.33. Двухвходовые нейроны сети могут иметь пороги Θ ∈ {3, 2}; однако при конфигурациях 6) и 7) сеть дает сбои: в первом случае с вероятностью р² (1 - р), а во втором - с вероятностью р³. Ниже будет показано (§ 4.6), что полностью надежные сети из двухвходовых нейронов не могут быть построены.

Основные принципы синтеза логически стабильных сетей изложены Мак-Каллоком в работе [13]. В настоящей работе основное внимание уделяется синтезу логически надежных сетей, имеющих, по мнению авторов, наибольший практический интерес.

Задача синтеза логически надежной сети сводится к следующему. Задана произвольная функция n переменных Φ (а₁,..., a_n) в § 1.3 показано, как эту функцию заменить эквивалентной ей одной вероятностной диаграммой n переменных, представляющей собой совершенную дизъюнктивную нормальную форму заданной функции. Эта диаграмма не содержит букв р и поэтому, являясь идеальной по надежности, не может быть задана для реализаций ее одним нейроном. В качестве первого шага синтеза надежной нейронной сети, вычисляющей заданную функцию Ф, необходимо идеальную вероятностную диаграмму D^ρ̄ заменить эквивалентной ей сетью максимально ненадежных вероятностных диаграмм. Под словами "максимальная ненадежность" понимается максимально допустимая занятость ячеек каждой диаграммы сети буквами р, еще не искажающая общего результата ее работы (т. е. не допускающая в результирующей диаграмме ни одной буквы р).

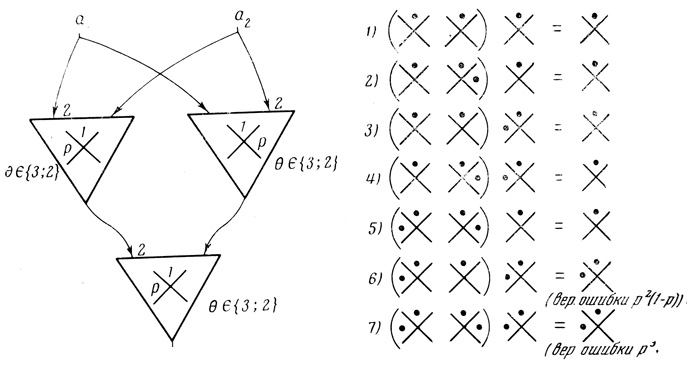
Рис. 4.33

Если формулу, вычисляемую сетью, обозначить через [Φ], то главным критерием правильности синтеза сети является эквивалентность этой формулы заданной, т. е.

Эта эквивалентность может быть достигнута только в том случае, если замена букв р на 1 или 0 в любой из ячеек диаграмм сети (независимо друг от друга) не повлияет на выдаваемый ею результат.

Прежде чем перейти к синтезу надежной нейронной сети из не-надежных нейронов, необходимо логическую функцию, заданную в произвольной форме, свести с СДНФ в виде одной идеальной диаграммы Венна. В § 1.3 были изложены принципы такого сведения, однако необходимо эту задачу формализовать в такой степени, чтобы она могла решаться при помощи ЭЦВМ. Это требование, естественно, будет являться общим для всех этапов синтеза надежной нейронной сети.

Наиболее простым методом ввода диаграмм Венна в ЭЦВМ и выполнения преобразований с ними является табличный метод.

Рассмотрим этот метод преобразования логической формулы к СДНФ на конкретном примере.

Пусть дана логическая функция Φ:

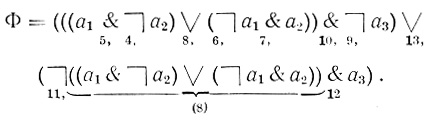
Построим таблицу, содержащую 2ⁿ столбцов и М строк. Столбцы перенумеруем с 0 до 2^n-1. Номер столбца соответствует номеру ячейки диаграммы Венна согласно принятым обозначениям в § 1, 1. Для каждой из n переменных, входящих в заданную логическую формулу Φ, отведем в таблице по одной строке. Для первой переменной ах отводится первая строка, которая заполняется символами {0, 1} так, что вначале проставляются подряд в ячейки таблицы 2^n-1 нулей и затем столько же единиц; для второй переменной отводится вторая строка, в которой проставляется 2^n-2 нулей и столько же единиц попеременно группами по 2^n-2 нулей и столько же единиц (вначале нули, а затем единицы) и т. д. для всех переменных. Так, для переменной а_n будет отведена строка с номером n, которая заполняется знаками 0 и 1 попеременно (так как 2^n-n = 1).

Рис. 4.34

Для проверки правильности записи полезно заметить, что если читать таблицу по столбцам сверху вниз, то с 0 по 2^n-1 номер столбца располагаются записанные в двоичном коде числа: 0,1,..., 2^n-1. Полученные n строк представляют собой табличную запись всех переменных, входящих в исходную формулу. Если рассматривать номера столбцов в качестве номеров ячеек в диаграмме Венна, то из диаграммного изображения переменных (рис. 4.34) можно сразу заполнить первые n строк таблицы.

Теперь необходимо по одной строке отвести на каждую элементарную операцию. Прежде чем приступить к заполнению этих последующих строк таблицы, необходимо на исходной логической формуле разметить последовательность выполнения операций в соответствии с правилами математической логики. Разметка предложенной в качестве примера формулы произведена в виде оцифровки операций, помещенной непосредственно под формулой.

Как видно из примера разметки, целесообразно не повторять уже проделанные операции, а лишь ссылаться на их номер, как это имеет место для операции (8).

Таким образом, последующие десять (для данного примера) строк (табл. 4.3) отводятся для выполнения логических операций, причем в результате последней из них на 13-й строке оказывается записанной искомая СДНФ в табличной записи. Принимая номера ячеек последней строки таблицы за соответствующие номера ячеек искомой диаграммы, получим СДНФ в виде одной идеальной вероятностной диаграммы Венна (рис. 4.35). Логические операции над строчками таблицы производятся для каждой ячейки в отдельности по существующим в математической логике правилам (т. е. в случае конъюнкции единица ставится только в том случае, если во всех ячейках сомножителей находится по единице; в случае дизъюнкции в результате ставится единица всегда, когда среди слагаемых есть хотя бы одна единица; при выполнении операции отрицания вместо 1 ставится 0 и наоборот).

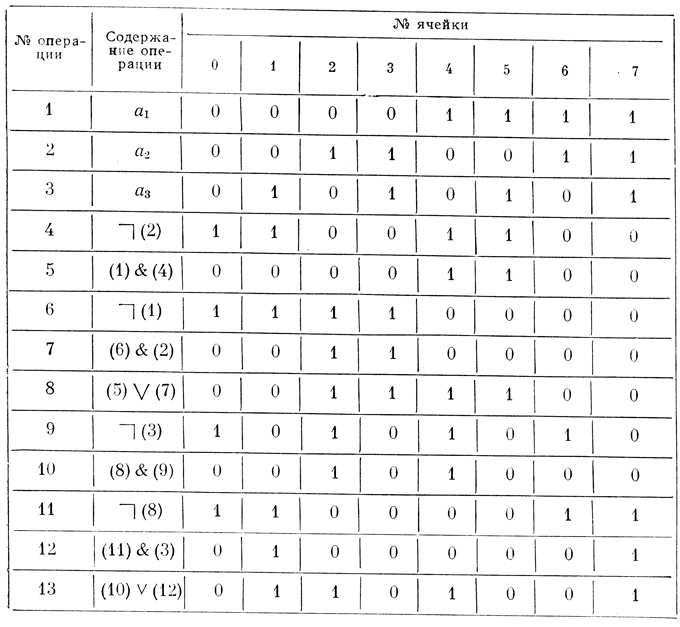
Таблица 4.3

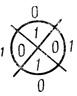
Рис. 4.35

Для простоты программирования таблицы все логические знаки, кроме ∨, &, сводятся к этим трем. Например, импликация a_1⊃a2 заменяется на а₁ ∨ а₂, штрих Шеффера а₁/а₂ на а₁ ∨ а₂ и т. д.