§ 4.6. Замена одной идеальной диаграммы двухранговой сетью ненадежных вероятностных диаграмм

Не представляет затруднений подобного типа таблицу построить для любого конечного числа переменных n и решать задачу совершенно формально при помощи таблицы "вручную", либо при помощи ЭЦВМ.

Рассмотрение вопроса о возможности построения надежной сети из ненадежных вероятностных диаграмм начнем с двухранговой сети двух переменных.

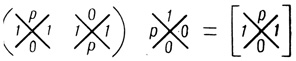
Рис. 4.36

Полный перебор всех возможных вариантов (в данном случае он невелик) построения сети, каждая диаграмма которой имеет хотя бы по одной ячейке, содержащей букву р, показывает, что надежный результат может быть получен только для двух случаев - при вычислении тавтологии или противоречия. Действительно, рассматривая, например, сеть рис. 4.36, легко убедиться, что, как бы ни переставлять букву р в диаграммах первого и второго рангов, все равно нельзя получить требуемой эквивалентности вычисляемой и заданной функции ([Φ] ≠ Φ): по крайней мере в одной из ячеек результата будет появляться буква р, что недопустимо.

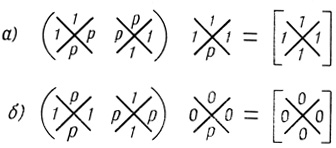
Рис. 4.37

Другое дело, если имеет место один из двух случаев, показанных на рис. 4.37. В первом из них оператор (р, 1, 1, 1) предписывает за- писать в результате единицы как в тех ячейках, где они есть в обеих диаграммах первого ранга, так и в тех, где они есть только в одной из них. Поэтому в результате [Φ] единицы есть во всех ячейках, т. е. без ошибки вычисляется тавтология.

Во втором случае, если в ячейке 0 оператора (р, 0, 0, 0) вместо р поставить единицу, в результате [Φ] единица могла бы появиться только в тех ячейках, в которых ее нет ни в одной из диаграмм первого ранга, но таких ячеек не существует; следовательно, во всех ячейках [Φ] будут только нули, т. е. без ошибки вычисляется противоречие. Однако тавтология и противоречие не несут нам никакой информации о мире и поэтому не представляют интереса.

Рассмотрим теперь построение по заданной идеальной диаграмме D^ρ̄ (а₁,а₂, а₃) двухранговой сети ненадежных вероятностных диаграмм.

Предварительно заметим, что для максимально допустимого числа ячеек ψ_r,i в которые может быть поставлена буква р без ухудшения требуемого результата, в работе [39] найдены выражения

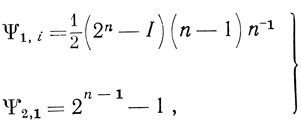
где I = 2ⁿ mod n (т. е. I - остаток от деления 2ⁿ на n). Нетрудно убедиться в том, что в одних диаграммах первого ранга число Ψ_1,i может быть увеличено за счет уменьшения его для других, однако из технических соображений желательно иметь Ψ_1,i примерно одинаковыми для всех диаграмм сети, что позволит предъявить менее жесткие требования к массовому производству технических нейронов, Из (4.26) следует, что для всех n Ψ_2,1>Ψ_1,i. Это соотношение имеет некоторый смысл: получается, что ненадежность выходного нейрона допускается более высокой, нежели ненадежность нейрона первого ранга.

Правила построения надежной сети из ненадежных вероятностных диаграмм рассмотрим на простейшем примере, когда заданная логическая функция преобразована к СДНФ а₁ а̄₂ а₃ ∨ а₁ а₂ а₃ в виде диаграммы D^ρ = (0, 0, 1, 0, 0, 1,0, 0).

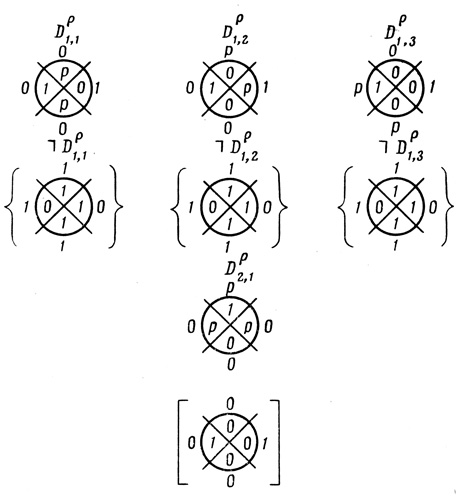
Рис. 4.38

1. Перенести из D^ρ̄ в соответствующие ячейки более половины диаграмм первого ранга (в данном случае - не менее двух) все единицы (рис. 4.38).

2. Построить отрицания диаграмм D^ρ_1,i, обозначаемые через D^ρ_1,i по правилу: в ячейках, одинаковых по номерам с теми, в которых у D^ρ_1,i стоят единицы, поставить нули и во всех остальных ячейках поставить единицы.

3. В диаграммах первого ранга разместить буквы р по числу не более чем Ψ_1,i = 1/2 (2ⁿ-I) (n - 1) n^-1 = 2; размещение произвести так, чтобы номера ячеек, в которых размещаются буквы для разных i, не пересекались. Из рис. 4.38 видно, что такое размещение может быть произведено в различных вариантах. Для случая n ≥ 4 это обстоятельство целесообразно учесть при составлении машинного алгоритма. Остальные ячейки диаграмм заполнить нулями.

4. Составить 2ⁿ логических произведений, по результатам которых заполнить ячейки оператора D^ρ_2,1, придерживаясь следующих правил:

а) если логическое произведение для каждой из одинаково пронумерованных ячеек совпадает с D^ρ̄, то в соответствующей по номеру ячейке оператора D^ρ_2,1 поставить единицу;

б) если логическое произведение тождественно равно нулю, то в соответствующей по номеру ячейке оператора D^ρ_2,1 поставить букву р;

в) в любом третьем случае (т. е. если логическое произведение не совпадает с D^ρ̄ и не равно нулю) в соответствующую по номеру ячей-ку оператора D^ρ_2,1 поставить нуль.

Эти правила вытекают из тех соображений, что в случае "б" наличие 0 или 1 не изменяет результат и поэтому в ячейку может быть поставлена буква р без искажения результата, а в случае "в" в ячейку необходимо поставить нуль, иначе будет искажена результирующая диаграмма [D^ρ̄] = [Φ].

Построим эти произведения для нашего примера в порядке возрастания номеров ячеек оператора:

1)

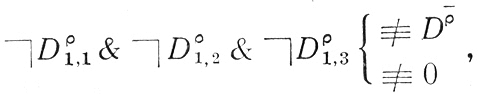
поэтому в ячейку 0 оператора ставим 0;

2)

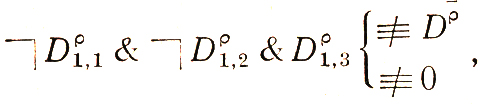
поэтому в ячейку 1 оператора ставим 0;

3)

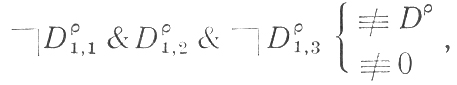
поэтому в ячейку 2 оператора ставим 0;

4)

D^ρ_1,1&D^ρ_1,2&D^ρ_1,3 ≡ 0,

поэтому в ячейку 3 оператора ставим букву р;

5)

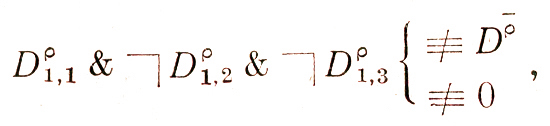
поэтому в ячейку 4 оператора ставим 0;

6)

D^ρ_1,1&D^ρ_1,2&D^ρ_1,3 ≡ 0,

поэтому в ячейку 5 оператора ставим букву р;

7)

D^ρ_1,1&D^ρ_1,2&D^ρ_1,3 ≡ 0,

поэтому в ячейку 6 оператора ставим букву р;

8)

поэтому в ячейку 7 оператора ставим 1.

На этом построение надежной сети из ненадежных вероятностных диаграмм заканчивается. Для проверки полученного результата по общим правилам работы сетей вероятностных диаграмм (§1,7) строим [D^ρ̄] и убеждаемся, что [D^ρ̄] = D^ρ и соответствующая итоговой диаграмме логическая функция [Φ] также эквивалентна заданной Φ : [Φ] = Φ; это является необходимым и достаточным условием правильного построения сети.

Решение описанной задачи на ЭЦВМ позволило бы строить сети для n = 3 и рассмотреть при этом максимальное число вариантов сетей, удовлетворяющих предъявляемым к ним требованиям. Для синтеза сети вероятностных диаграмм по заданной диаграмме при помощи ЭЦВМ изложенную задачу формализуем в виде таблицы. Решение рассмотренной выше задачи сведено к табл. 4. 4. Таблица имеет (2ⁿ + 1) столбцов и (2ⁿ + 2n + 1) строк. В последнем столбце помещается вычисленное значение D^ρ_2,1. В первой строчке записывается заданная диаграмма D^ρ̄ в каждой ячейке табличной строки ставится знак (0,1 или р) из соответствующей по номеру ячейки диаграммы D^ρ̄. Строчки со 2-й по (n + 1) предназначены для записи D^ρ_1,i, с (n + 2) по (2ⁿ + 1) - для записи и с (2ⁿ + 2) по (2ⁿ + 2n + 1) - для записи логических произведений, которые в развернутом виде были показаны на стр. 235.

Работа с таблицей сводится к следующему,

1. В первую строку записывается заданная диаграмма D^ρ̄.

2. Все единицы и р (если они есть^*) из первой строки переносятся в строки с D_1,i:

а) в первом цикле расчетов - во все n строк с D^ρ_1,i,

5) во втором цикле расчетов - в (n - 1) строк и т. д., но не менее чем в > n/2 строк (т. е. в данном примере не менее чем в две строки).

3. В строках с D^ρ_1,i ячейки, соответствующие п. 2, заполняются нулями, а все оставшиеся после этого свободные ячейки этих строк заполняются единицами.

4. Возвращаясь к строкам с ?)?/, расставляем в часть свободных ячеек буквы р^**; расстановка р задается вспомогательной таблицей (табл. 4.5) и повторяется в каждом цикле вычислений в соответствии с заданной машине программой перебора. В табл. 4.5 одинаковыми цифрами показаны ячейки, в которых одновременно размещаются р, а цифра показывает очередность размещения внутри данного цикла вычислений. В заполненную ячейку буква р не ставится.

^* (Оговорка относительно р касается построения многоранговой сети, которая будет рассмотрена ниже.)

^** (Для ввода в машину буква р кодировалась цифрой 3 в столбцах с 1-го по 2ⁿ - 1 и цифрой 4 в последнем столбце.)

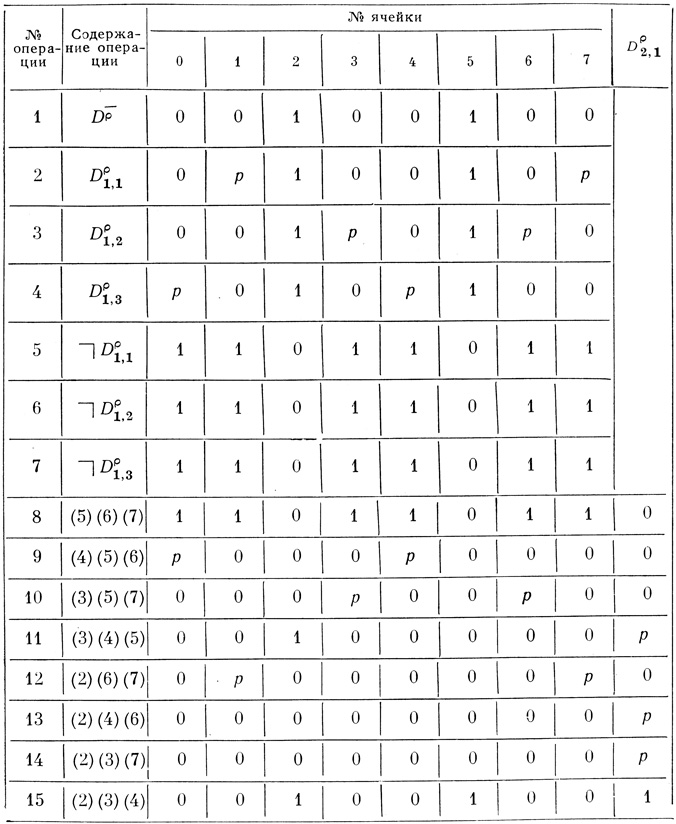
Таблица 4.4

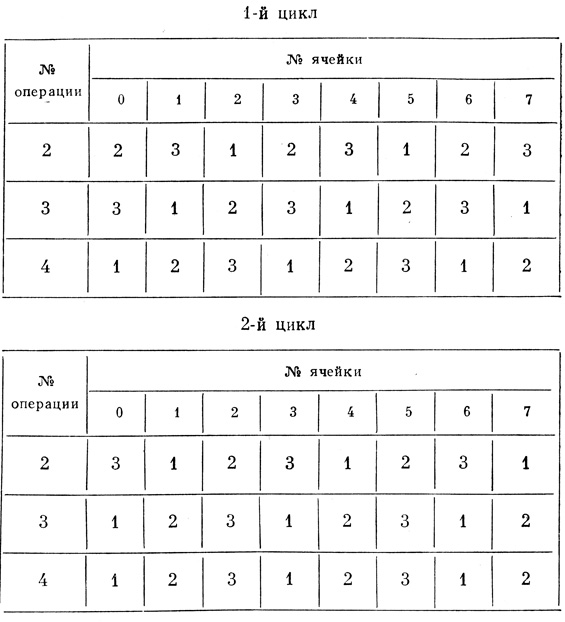
Таблица 4.5

Все оставшиеся после размещения букв р ячейки заполняются нулями.

Для каждого варианта размещения р производится реализация алгоритма до конца.

5. В строках с (2ⁿ + 2) до (2ⁿ + 2n + 1) (для нашего примера строки 8-15) производятся логические умножения; при этом имеется в виду, что р×р×1 = р×р×р = р.

В зависимости от результатов, полученных в каждой строке, в последней ячейке ее, принадлежащей столбцу D^ρ_2,1, записывается:

а) в случае, если элементы данной строки совпадают с элементами 1-й строки (т. е. с D^ρ̄),- единица;

б) в случае, если во всех ячейках данной строки стоят нули,- буква р;

в) во всех остальных случаях - нуль.

6. Если после заполнения таблицы в ячейках последнего столбца (D^ρ_2,1) окажется хотя бы одна единица,- результат выдается на печать.

Результатом, выдаваемым на печать, является:

а) n строк, содержащих D^ρ_1,i (в данном примере строки 2, 3 и 4);

б) последний столбец, содержащий D^ρ_2,1 (в данном примере столбец 9).

Для построения диаграмм первого ранга D^ρ_1,i номер ячейки каждой из строк (со 2-й по 4-й) принимается за соответствующий номер ячейки искомых диаграмм; для построения диаграммы D^ρ_2,1 читаем запись в ячейках последнего столбца сверху вниз и принимаем порядковый номер ячейки за соответствующий номер ячейки искомой диаграммы D^ρ_2,1.

7. Для получения максимального числа возможных сетей (если это нужно) после каждой реализации возвращаемся к п. 4) для нового варианта размещения букв р.

8. После полного перебора всех предусмотренных программой вариантов расположения р возвращаемся к п. 26, т. е. к новому циклу расчетов, когда единицы (и р, если они есть) из 1-й строки переносятся теперь уже не в n последующих строк, а в (n - 1) строк; последний цикл расчетов должен закончиться, когда перенос произведен в число строк, составляющих не менее половины величины n.

Таким образом, машинная реализация алгоритма позволяет выдать на печать множество вариантов сетей диаграмм типа D^ρ_r,i, из которых можно выбрать сети, содержащие максимально допустимое число ячеек сри выполняющих заданную логическую формулу Φ = D^ρ̄ без ошибок. Проверка всех полученных таким путем сетей показывает, что [Φ] = Φ и сети, таким образом, составлены правильно.

Описанный алгоритм запрограммирован для реализации его на ЭЦВМ УРАЛ-2 для n = 4. Несколько примеров реализации функции Φ = а₁ā₂ā₃ā₄ ∨ a₁a₂a₃ā₄ показано на рис. 4.39.

В тех случаях, когда в диаграмме D^ρ̄ количество занятых единицами ячеек ≥ 2^n-1, может оказаться невозможным обеспечение желательной одинаковости числа ячеек ψ_r,1 (в диаграммах одного ранга), в которые без искажения результата можно разместить буквы р. При этом требуемый результат может быть достигнут за счет построения выходной вероятностной диаграммы (в двухранговой сети - диаграммы D^ρ_2,1), количество ячеек которой, содержащих единицы, больше единицы.

Рассмотрим пример изменения изложенных правил, позволяющий построить такую сеть для n = 3.

Пусть задана диаграмма D^ρ̄ = (0, 0, 0, 1; 0, 1, 1, 1). Требуется построить двухранговую сеть вероятностных диаграмм D^ρ_r,1, у которой операторная диаграмма D^ρ_r,1 имеет более чем одну ячейку с содержанием единицы. Построение производим при помощи стандартной таблицы по следующим правилам.

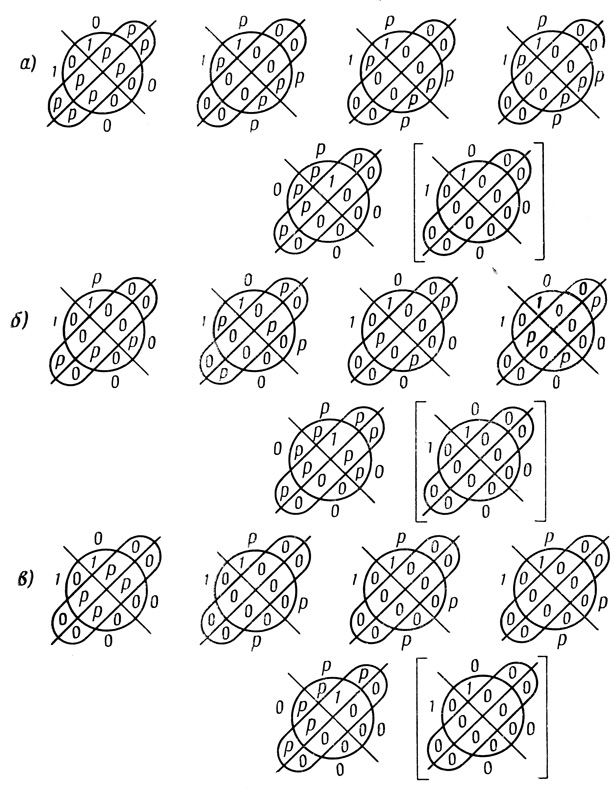
Рис. 4.39

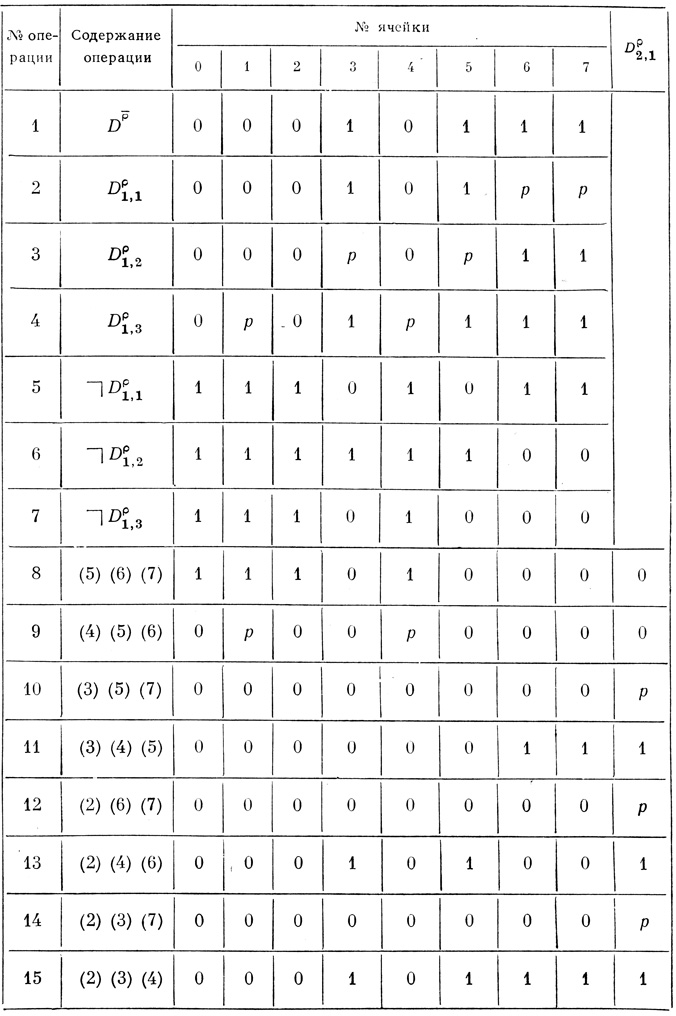
Таблица 4.6

1. Записываем исходную диаграмму в первую строку таблицы (табл. 4.6).

2. Во второй строке:

а) сносим единицы из половины (по числу) ячеек первой строки, занятых единицами;

б) вместо остальных единиц первой строки сносим во вторую строку буквы р (в данном примере в ячейках 4 и 6 второй строки помещаем единицы, а в 7 и 8 - буквы р; можно принять и любой другой порядок размещения 1 и р, отвечающий этому правилу).

3. В третьей строке вместо букв р снести единицы и, наоборот, в ячейки, соответствующие тем, в которых во второй строке стоят единицы, в третьей поставить буквы р (в данном случае в ячейках 4 и 6 третьей строки помещаем буквы р, а в ячейках 7 и 8 - единицы).

4. В четвертой строке:

а) сносим все единицы из первой строки;

б) ставим в Ψ_1,i любых пока свободных ячеек буквы р (здесь Ψ_1,i = 2).

5. Во все оставшиеся свободными ячейки строк 2, 3, 4 ставим нули.

6. Далее действуем в соответствии с п. 5-8 правил, изложенных на стр. 238.

Рис. 4.40

В результате получаем сеть вероятностных диаграмм (рис. 4.40), в которой оператор имеет уже не одну (как раньше), а три ячейки, содержащие единицы.

Варьируя размещением 1 и р в рамках правил 2 и 4, можно получить некоторое множество вероятностных сетей D^ρ_r,i, каждая из которых выполняет заданную диаграмму D^ρ̄. Исходя из каких-либо дополнительных требований или же произвольно, из них можно выбрать один вариант диаграмм D^ρ_r,i, по которому и производить дальнейший синтез надежной нейронной сети.