§ 4.7. Переход от вероятностных диаграмм к порядковым и пороговым

После реализации алгоритма, описанного в предыдущем пара-графе, заданная логическая функция Φ (а₁, ...,а_n) выражается сетью не надежных диаграмм вероятностного типа D^ρ_r,i.

По методикам, изложенным в третьей главе, синтез оптимальных (в некотором смысле) нейронов производится по их пороговым диаграммам D^θ_r,i. Однако для перехода от сети D^ρ_r,i вероятностных диаграмм к сети пороговых целесообразнее всего пройти через промежуточный этап - построение сети диаграмм порядкового типа. Как уже отмечалось, диаграмма порядкового типа показывает последовательность, в которой добавляются точки в ячейках по мере снижения порога срабатывания формального нейрона от противоречия до тавтологии.

Будем рассматривать как невырожденные порядковые диаграммы, так и частично вырожденные, т. е. такие, у которых на некоторых диапазонах изменения порога снижение порога на единицу ведет к появлению сразу двух или более точек или совсем не приводит к изменению их числа. В порядковых диаграммах вырожденность проявляется в наличии нескольких ячеек с одинаковыми порядковыми числами.

Определяющими при расстановке порядковых чисел в ячейках диаграммы являются следующие соображения. Известно, что 0 ≤ р ≤ 1 и, следовательно, высшие пороги должны соответствовать ячейкам, занятым единицами, а низшие - ячейкам, занятым нулями; ячейкам, содержащим буквы р, должны соответствовать промежуточные значения порогов. Заметим, что вырождение приводит к уменьшению общего количества волокон W и поэтому применяется там, где это допустимо; однако использовать вырождение для ячеек, содержащих р, невыгодно, так как оно приведет к сужению диапазона допустимых значений порога Θ ∈ {β₁ ,..., β_k}. Вместе с тем для диаграмм с n ≥ 4, для которых величина Ψ_r,i достаточно велика, иногда бывает целесообразным допустить частичное вырождение и для ячеек, занятых буквами р, что дает снижение числа волокон W. Исходя из изложенных предпосылок, заполнение порядковой диаграммы начинаем с нумерации ячеек, которым в вероятностной диаграмме соответствуют ячейки, содержащие единицы; при этом все эти ячейки можно занумеровать одной цифрой (если отсутствуют соображения, требующие вообще не допустить вырождения); затем необходимо перенумеровать ячейки, соответствующие занятым в вероятностной диаграмме буквами р (по одному номер на ячейку - если не хотим допустить вырождение); наконец, нумеруем ячейки, соответствующие заполненным нулями в вероятностной диаграмме (один номер ставим, если допускаем для этих ячеек вырождение и каждой ячейке отводим по одному номеру, если не допускаем). На рис. 4.41 для вероятностной диаграммы D^ρ = (0, 0, 0, р, 0, р, р, 1) (рис. 4.41,а) показаны порядковые диаграммы с вырождением (рис. 4.41, б и б) и без вырождения (рис. 4.41, г) На рис. 4.42 показаны соответствующие порядковые диаграммы еще для одного случая, когда D^ρ = (р, р, р, 0, 1, 0, 0, 1).

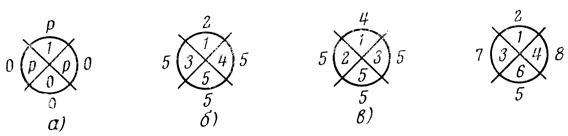
Рис. 4.41

Из последних двух примеров видно, что правила построения порядковой диаграммы неоднозначны, так как не указан порядок нумерации ячеек, соответствующих по номерам тем, в которых вероятностная диаграмма содержит буквы р. Вместе с тем завершение синтеза нейрона с минимальным числом волокон Ŵ (или ветвей V̂) показывает, что последнее зависит от порядка нумерации ячеек в порядковой диаграмме D^π_r,i.

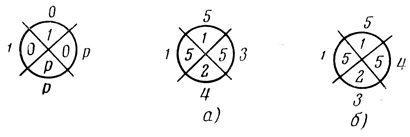
Рис. 4.42

В настоящее время эта связь установлена эмпирическим путем и лучший вариант выбирается в результате перебора всех возможных вариантов нумерации ячеек, занятых буквами р. Установление аналитической или логической зависимостей минимального числа волокон Ŵ (или ветвей V̂) от порядка нумерации ячеек в порядковых диаграммах является одной из нерешенных актуальных задач теории нейронных сетей. Следующим шагом после перехода от сети вероятностных диаграмм к сети порядковых диаграмм является переход от сети порядковых диаграмм к сети пороговых диаграмм.

После реализации последнего алгоритма получена сеть из порядковых диаграмм D^π_r,i. Задача теперь сводится к замене каждой из порядковых диаграмм пороговой диаграммой и определению допустимого множества значений порогов Θ ∈ β(β₁,..., β_k) для каждой из пороговых диаграмм.

Для решения этих задач необходимо: а) иметь заполненную диаграмму D^π_r,i; б) знать определение диаграммы D^θ_r,i; в) учесть, что в нулевой ячейке любой пороговой диаграммы всегда помещается нуль (так как эта ячейка соответствует входной последовательности а₁ & а₂ & .... а_n). Заполнение каждой из пороговых диаграмм D^θ_r,i необходимо производить по следующим правилам, вытекающим из определения диаграмм порогового типа:

1) в нулевую ячейку D^θ_r,i поставить γ₀ = 0;

2) в ячейки D^θ_r,i имеющие в соответствующих по номерам ячейках порядковой диаграммы D^π_r,i, уменьшающуюся нумерацию (речь идет не о принятой нумерации ячеек, а о числах, стоящих в ячейках порядковой диаграммы), проставить значения γ_j, последовательно увеличивающиеся на единицу, начиная с нуля в нулевой ячейке;

3) в ячейки D^θ_r,i, имеющие в соответствующих по номерам ячейках порядковой диаграммы D^π_r,i возрастающую нумерацию, проставить значения последовательно уменьшающиеся на единицу, начиная с нуля в нулевой ячейке (т. е. все эти значения будут отрицательными);

4) в ячейки D^θ_r,i имеющие в нескольких соответствующих по номерам ячейках порядковой диаграммы одинаковые числа, разместить одинаковые значения γ_j;

5) для каждой из построенных таким образом пороговых диаграмм D^θ_r,i определить множество допустимых значений порогов Θ ∈ β{β₁, ..., β_k}; допустимыми являются только те значения β_i ≡ γ_j, которые обеспечивают срабатывание нейрона при входных последовательностях, соответствующих ячейкам, содержащим в вероятностной диаграмме D^θ_r,i только единицы и буквы p, но ни в коем случае не нули.

Для иллюстрации изложенных правил построим пороговую диаграмму для D^π, показанной на рис. 4.42, б:

Необходимо построить пороговую диаграмму D^θ и определить допустимое множество значений порогов Θ ∈ β{β₁ ,..., β_k}.

Решаем эту задачу в соответствии с изложенными правилами 1-5:

1) в нулевую ячейку, занятую в порядковой диаграмме числом 3, ставим 0 (рис. 4.43, а);

2) в соответствии со вторым правилом в ячейку 1 ставим γ₁ = 1 и в ячейки 4 и 7 ставим γ₂ = γ₇ = 2 (рис. 4.43, б);

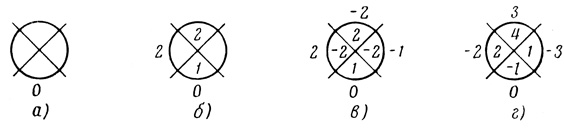
Рис. 4.43

3) в соответствии с третьим правилом в ячейку 2 ставим γ₂ = -1 и в ячейки 3 и 6 ставим γ₃ = γ₆ = - 2 (γ₄ = γ₇ и γ₃ = γ₆ на основании правила 4), на этом построении пороговой диаграммы заканчивается (рис. 4.43, в);

4) в соответствии с пятым правилом устанавливаем, что Θ ∈ β{2; 1; 0; - 1}.

На рис. 4.43, г приведен еще один пример построения пороговой диаграммы по порядковой диаграмме, показанной на рис. 4.41, г.

Заметим, что пороговая диаграмма по заданной порядковой строится вполне однозначно.