§ 4.8. Замена одной идеальной диаграммы многоранговой сетью ненадежных вероятностных диаграмм

При анализе двухранговой сети из пороговых диаграмм может оказаться, что полученные при переходе к D^θ_r,i допустимые диапазоны разброса порогов Θ ∈ β{β₁,....,β_k} не достигают аналогичных величин у конкретных технических нейронов, предназначенных для реализации заданной функции. В этом случае расширение диапазонов Θ до необходимых пределов можно произвести за счет увеличения числа рангов сети. Сделать это можно по тому же алгоритму, который был описан в § 4.6 для построения двухранговых сетей. Построение многоранговой сети сводится к выполнению следующей последовательности правил.

1. По алгоритму для построения двухранговой сети вероятностных диаграмм (§ 4.6) для заданной диаграммы D^ρ̄ на ЭЦВМ табличным способом построить допустимые варианты двухранговой сети D^ρ_r,i (шаг 1).

2. Из полученных допустимых вариантов D^ρ_r,i выбрать такой, у которого в диаграммах первого ранга D^ρ_1,iколичество ячеек, занятых буквами р, относительно больше, чем в диаграмме D^ρ_2,1. Такой первый ранг принять за первый ранг искомой многоранговой сети.

3. Найденную таким путем диаграмму D^ρ_2,1 принять за новую результирующую диаграмму (которую из-за наличия в некоторых ее ячейках букв р обозначим через D^ρ₁) и по тому же алгоритму построить новую двух ранговую сеть, осуществив тем самым шаг 2. Здесь уместно напомнить о замечании, сделанном на стр. 236, касающемся заполнения первой строки таблицы, когда в ячейках диаграммы D^ρ, помимо единиц и нулей, есть еще и р; при выполнении второго шага таблица может быть заполнена правильно только с учетом этого замечания. Полученные в результате шага 2 диаграммы первого ранга необходимо принять за второй ранг искомой много-ранговой сети D^ρ_r,1, а вновь полученная выходная диаграмма является D^ρ_3,1, и, таким образом, оказывается построенной трех ранговая сеть.

4. Если требуется построить четырех ранговую сеть, то найденную на предыдущем шаге диаграмму D^ρ_3,1 принять за новую результирующую диаграмму D^ρ₂ и произвести шаг 3 по тому же алгоритму; в результате этого шага определяются ранг диаграмм D^ρ_3,1 и новая выходная диаграмма D^ρ_4,1.

5. Построение диаграмм последующих рангов производить по тем же правилам 1-4. Заметим, что изложенные правила построения много ранговой сети вероятностных диаграмм не являются однозначными: по ним может быть построен ряд сетей, выполняющих заданную функцию D^ρ̄, но различающихся количеством букв р в диаграммах и порядком их размещения в ячейках диаграмм.

Из технических соображений бывает желательным иметь в диаграммах (по крайней мере для данного ранга) примерно одинаковое но максимально допустимое количество ячеек, занятых буквами р. Этим соображением и рекомендуется руководствоваться при замене одной идеальной диаграммы сетью ненадежных диаграмм вероятностного типа, необходимых для дальнейшего построения как двух ранговых, так и много-ранговых надежных сетей. Для иллюстрации изложенных правил построения много-ранговой вероятностной сети построим трех ранговую сеть, реализующую функцию Φ = а₁а̄₂a₃ ∨ ā₁a₂ā₃ с диаграммой D^ρ̄ = (0, 0, 1, 0, 0, 1, 0, 0).

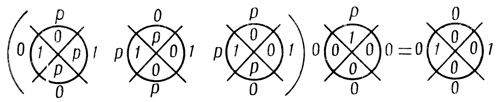
Рис. 4.44

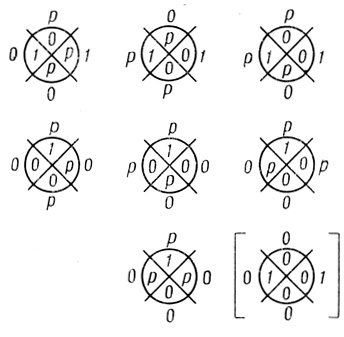
Рис. 4.45

При помощи табл. 4.7 и 4.8 осуществляем шаги 1 и 2 (пункты 1-3 правил), в результате чего получаем после шага 1 промежуточную двух ранговую сеть (рис. 4.44) и искомую трех ранговую сеть вероятностных диаграмм D^ρ_r,i (рис. 4.45),

Для построения соответствующей нейронной сети каждая диаграмма много-ранговой вероятностной сети (так же как и двух ранговой) должна быть последовательно заменена порядковой и затем пороговой диаграммами. Правила такого перехода были изложены в § 4.7.

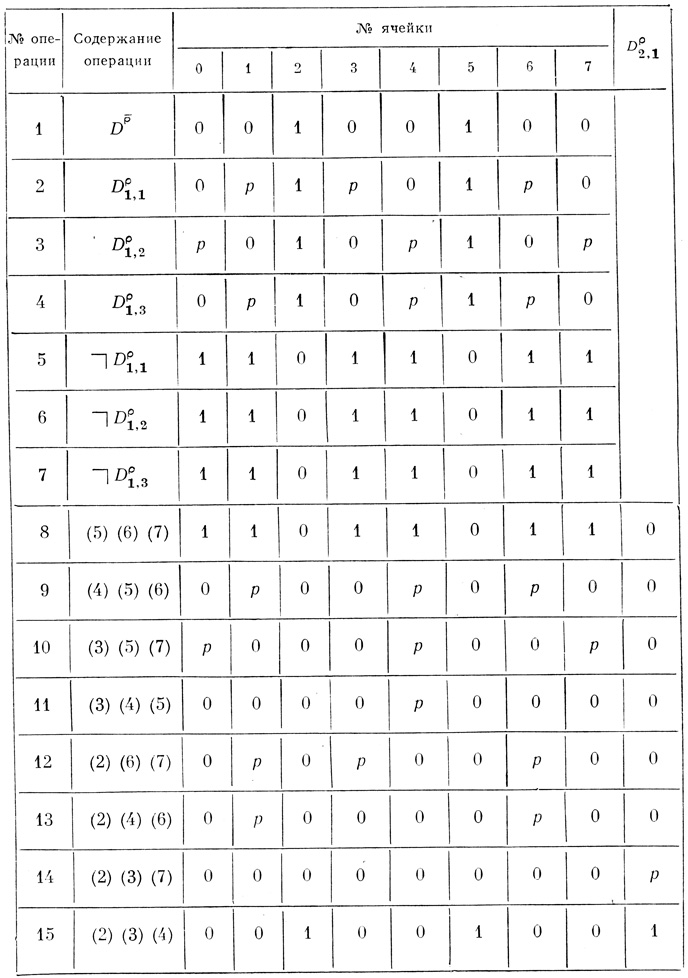
Таблица 4.7

Таблица 4.8