§ 4.9. Построение надежных сетей из формальных нейронов

После составления сети пороговых диаграмм, реализующих заданную функцию Φ (а₁, ..., а_n), остается выполнить последний шаг - синтез по каждой из диаграмм D^θ_r,i оптимального (в некотором смысле) формального нейрона, занимающего в нейронной сети место в соответствии с той пороговой диаграммой, по которой он синтезирован.

Как уже отмечалось ранее, синтезировать нейрон - значит так определить все его волокна по типам, входам и количеству, чтобы его функционирование происходило в соответствии с заданной (в данном случае - пороговой) диаграммой.

Для перехода от сети пороговых диаграмм к оптимальной нейронной сети необходимо задаться критерием оптимальности в соответствии с § 3.3.

Рассмотрим на конкретном примере последовательную реализацию всех правил, позволяющих для произвольно заданной логической функции Φ (а₁, ..., а_n) построить оптимальную сеть из формальных нейронов.

Пусть задана функция

Требуется построить нейронную сеть, надежно реализующую заданную функцию при разбросе пороговых значений в нейронах не менее чем в три единицы; все нейроны сети должны быть оптимальны или (если оптимальность недостижима) минимум ветвей V̂_r,i и относительный минимум волокон W̃_r,i.

1. Для заданной функции Φ (а₁, а₂, а₃) построим ее совершенную дизъюнктивную нормальную форму в виде одной идеальной диаграммы вида D^ρ̄ Для этого воспользуемся правилами, изложенными в § 4.5, в результате чего получим диаграмму D^ρ̄ = (0, 0, 1, 0, 0, 1, 0, 0).

В связи с простотой данного примера построение можно проделать при помощи таблицы типа табл. 4.3 без обращения к ЭЦВМ. В общем случае (особенно при n > 4) эта часть алгоритма построения надежной сети (как и все последующие) может реализоваться на ЭЦВМ.

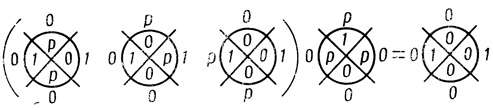
Рис. 4.46

2. Полученную диаграмму D^ρ̄ при помощи правил, изложенных в § 4.6, заменяем двух ранговой сетью ненадежных вероятностных диаграмм D^ρ_r,i (рис. 4.46).

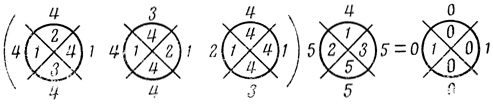
Рис. 4.47

3. Сеть вероятностных диаграмм D^ρ_r,i при помощи правил, изложенных в § 4.7, заменяем сетью порядковых диаграмм D^π_r,i (рис. 4.47).

4. Полученную сеть порядковых диаграмм D^π_r,i в соответствии с правилами, изложенными в § 4.7, заменяем сетью пороговых диаграмм D^θ_r,i, одновременно для каждой из пороговых диаграмм определяем диапазон допустимых изменений пороговых величин Θ_r,i ∈ β{β₁,....,β_k}. Полученная таким образом сеть диаграмм с соответствующими значениями Θ_r,i показана на рис. 4.48.

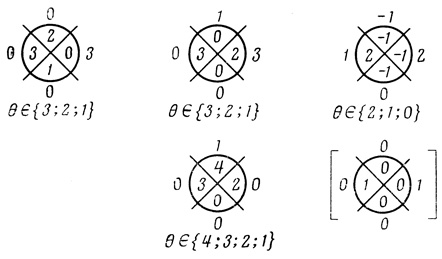
Рис. 4.48

5. По каждой из диаграмм сети D^θ_r,i синтезируем оптимальный нейрон:

а) при помощи автоматического синтеза оптимальных нейронов (§ 3.7) находим параметры H_i, позволяющие непосредственно вычертить нейрон с минимальным числом волокон Ŵ̂ и ветвей V̂̂ одно-временно. В качестве исключения будем допускать нейроны с минимальным числом ветвей V̂ и относительным минимумом волокон W̃.

Непосредственно с ленты ЭЦВМ строим нейронную сеть, показанную на рис. 4.49;

б) для контроля полученных результатов по каждой из пороговых диаграмм находим минимальное число волокон Ŵ, используя для этого симплексный метод (§ 3.4.). В данном случае оказалось

Ŵ_1,1 = 17, Ŵ_1,2 = 21, Ŵ_1,3 = 16, Ŵ_2,1 = 14, что полностью совпадает с результатами автоматического синтеза (рис. 4.49).

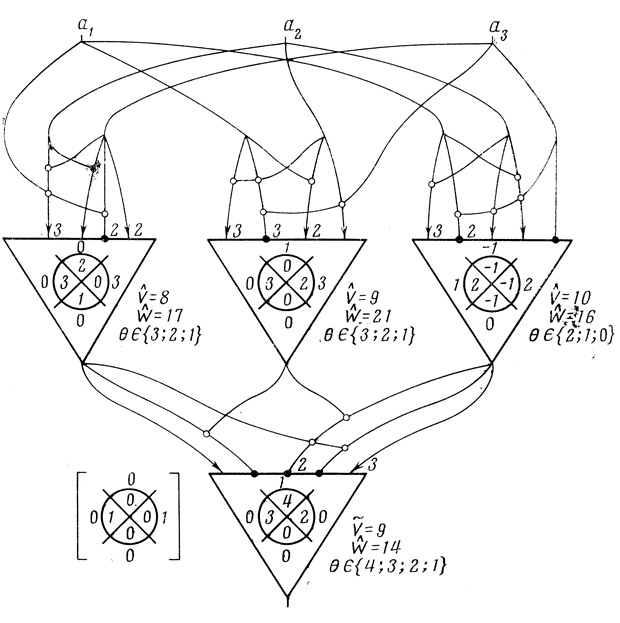
Рис. 4.49

Аналогичным путем может быть синтезирована и много-ранговая сеть D^ρ_r,i для выполнения той же функции. Для ее построения сеть надо было бы синтезировать по правилам § 4.8, а всю остальную работу для каждой из диаграмм много-ранговой сети D^ρ_r,i выполнить в той же последовательности, что и для приведенного примера. На рис. 4.50 показана трех ранговая нейронная сеть, реализующая ту же заданную функцию Φ(а₁, а₂, а₃) = а₁а̄₂а₃ ∨ ā₁a₂ā₃.

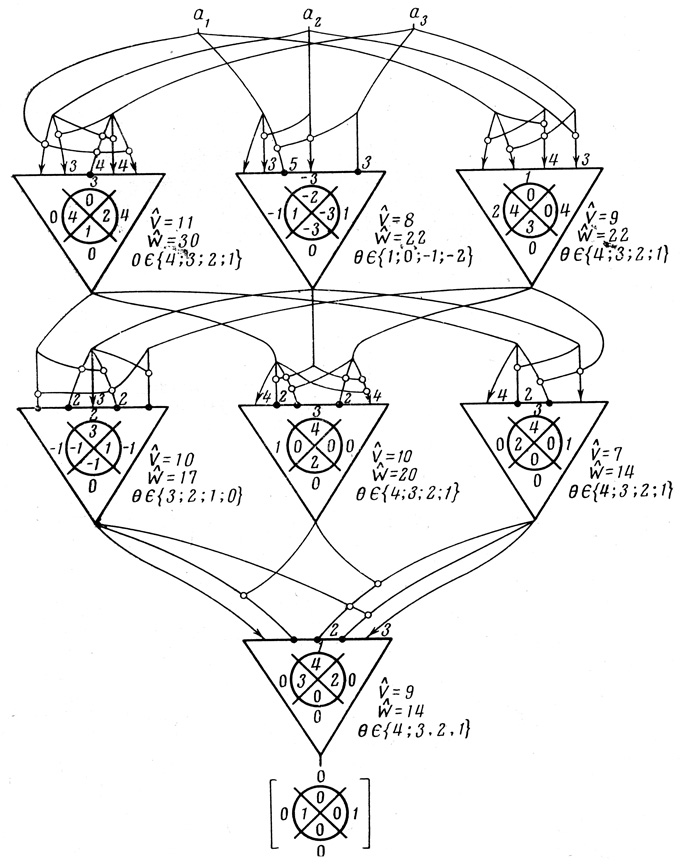
Рис. 4.50