Глава 5. Некоторые вопросы технических приложений

§ 5.1. Сравнение логических возможностей формальных нейронов и пороговых элементов

Формальный нейрон является моделью нервной клетки. В его описании (§ 0.3; 2.2) отражены лишь некоторые черты живого нейрона, которые играют важную роль в переработке информации нервной системой и которые могут найти применение при создании устройств более надежных, чем составляющие их части.

Проблема построения надежных устройств из относительно малонадежных элементов решалась в [14]. Однако, как отмечается в [16], для предложенного в [14] решения требуются элементы, более надежные по сравнению с клетками мозга человека. Этим в [16] объясняется необходимость введения формального нейрона. Объяснение представляется интересным. На наш взгляд, в этом направлении должна быть проделана большая работа, особенно по установлению более четких критериев сравнения формальных моделей с соответствующими элементами живых организмов.

Кроме того, различные модели (прежде всего в некотором смысле наиболее близкие) можно сравнивать непосредственно между собой. Так, формальный нейрон можно рассматривать как обобщение порогового элемента.

Пороговый элемент отличается, как указывалось в § 0.2, от нейрона тем, что, во-первых, у него нет запрещающих волокон, во-вторых, порог фиксирован, т. е. интервал изменения порога состоит только из одного числа. Так как в живых организмах имеется аналог запрещающих волокон [12] и пороги нервных клеток не остаются не измененными, а в зависимости от ряда факторов флуктуируют, то-формальный нейрон более точно моделирует функционирование живого нейрона, нежели пороговый элемент. Сравним между собой формальные нейроны и пороговые элементы, взяв за основу сравнения реализацию формул исчисления высказываний на одном формальном нейроне и на одном пороговом элементе.

В § 3.8 показано, что любую формулу исчисления высказываний можно реализовать на одном формальном нейроне, т. е. для любой формы Φ исчисления высказываний можно построить нейрон А, возбуждающийся при некотором значении порога Θ = Θ₀ тогда и только тогда, когда формула Φ принимает значение 1.

Пороговая диаграмма построенного нейрона А такова, что

где β₁,....,β_s - номера ячеек, в которых на диаграмме D^ρ̄ (n), соответствующей формуле Φ, находятся единицы;

Перейдем к вопросу о реализации формул исчисления высказываний на одном пороговом элементе.

Пусть Φ - формула исчисления высказываний, составленная из переменных а₁, ..., а_n. Пороговая диаграмма, соответствующая формуле Φ, строится неоднозначно (см. § 3.8).

Если Φ = 0 или Φ = 1, то формула Φ реализуется на пороговом элементе без волокон с порогом Φ = 1 в первом случае (когда Φ = 0) и Θ = 0 во втором случае (когда Φ = 1).

Рассмотрим случай, когда Φ не является ни тождественно ложной, ни тождественно истинной формулой (Φ ≠ 1; Φ ≠ 0).

Если среди пороговых диаграмм, соответствующих формуле Φ, можно найти такую диаграмму, по которой конструируется нейрон без запрещающих волокон, то формула Φ реализуется на одном пороговом элементе.

Действительно, предположим, что нам удалось найти пороговую диаграмму, по которой можно построить нейрон без запрещающих волокон. Построим такой нейрон А, возьмем интервал изменения порога нейрона А, состоящий из одного числа θ₀ = γ_min (γ_min определяется аналогично § 3.8), получим, что А есть пороговый элемент, возбуждающийся тогда и только тогда, когда формула Φ принимает значение 1.

Таким образом, вопрос о реализации формул исчисления высказываний на одном пороговом элементе сводится к нахождению такой пороговой диаграммы D^θ, которая соответствует формуле Φ и по которой можно построить нейрон без запрещающих волокон.

Используя аналитические выражения формальных нейронов, получим, что по данной пороговой диаграмме n переменных можно синтезировать нейрон без запрещающих волокон тогда и только тогда, когда все числа γ_α1,...,γ_αn где α₁,...,α_n - номер ячейки диаграммы записанный в двоичной системе, удовлетворяют условию

(в индексах букв γ по одной единице и n = 1 нулей).

Представляя индексы букв у в десятичной системе, перепишем условие (5.1):

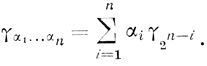(5.2)

Из § 3.8 и (5.2) следует, что по диаграмме D^ρ̄, соответствующей данной формуле Φ, можно построить пороговую диаграмму D^θ, по которой синтезируется нейрон без запрещающих, волокон тогда и только тогда, когда система s (2ⁿ - s) неравенств

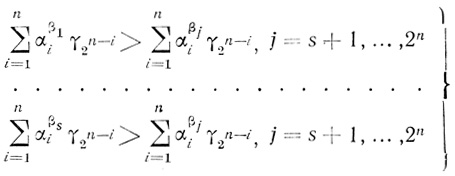(5.3)

непротиворечива, где γ_t - переменная (соответствующая числу в i-той ячейке на D^θ), t = 2⁰, ..., 2^n-1; α^β_ii равно единице или нулю в зависимости от того, принадлежит ячейка номер β_i на D^ρ̄ i-той фигуре или ее дополнению, l = 1, ..., 2ⁿ.

Следовательно, для того чтобы проверить, реализуется данная формула Φ исчисления высказываний на одном пороговом элементе или нет, составляем систему s (2ⁿ - s) неравенств (5.3). Возможны два случая.

1. Система (5.3) непротиворечива. Тогда можно построить пороговый элемент А (n), на котором реализуется заданная формула Φ. Построение порогового элемента А (n).

Возьмем любое целочисленное решение системы (5.3):

числа δ₁, ..., δ_n выбираем по возможности меньшими по модулю (для такой выборки удобно использовать ЭЦВМ).

От i-того входа на тело проводим тормозящее волокно с весом |δ_i|, если δ_i<0.

От j-того входа на тело проводим возбуждающее волокно с весом δ_j, если δ_j>0.

k-тый вход является фиктивным, если δ_k = 0.

где γ_Bj - число в ячейке номер β_i на пороговой диаграмме нейрона А (n), при этом β_j является также номером ячейки, в которой на диаграмме β_j/D^ρ̄, соответствующей формуле Φ, находится единица, j = 1,....., s, s - число ячеек, в которых на D^ρ̄ расположены единицы (s > 0, так как ФΦ ≠ 0).

2. Система (5.3) противоречива. Тогда формулу Φ нельзя реализовать на одном пороговом элементе. Для реализации формулы Φ можно использовать формальный нейрон, который обязательно будет иметь запрещающие волокна.

Построение нейрона, на котором реализуется данная формула Φ, можно осуществлять описанными выше методами (связанными с предварительными переходами к пороговым диаграммам). Кроме этого, можно пользоваться способом, непосредственно следующим из § 3.8.

Пусть Ω_n - аналитическое выражение n переменных с неопределенными коэффициентами; для определенности будем считать, что Ω_n принадлежит первому классу.

Результат подстановки значений переменных из некоторой элементарной последовательности в Ω_n есть сумма неопределенных коэффициентов, которую обозначим w_n,j, где j - номер рассматриваемой элементарной последовательности.

Например, если имеет вид (3.7), то

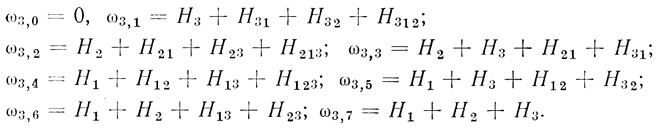
Из § 3.8 вытекает следующая система неравенств, которой должны удовлетворять значения коэффициентов Ω_n, чтобы на нейроне, соответствующем Ω_n, можно было бы реализовать формулу Φ:

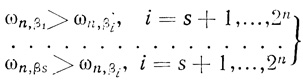(5.4)

где β₁, ..., β_s - номера ячеек на диаграмме D^ρ̄ (n), соответствующей формуле Φ, в которых находятся единицы.

По любому целочисленному решению системы (5.4) можно спроектировать (в силу соответствия между формальными нейронами и аналитическими выражениями) нейрон, на котором реализуется данная формула Φ. В частности, можно находить и оптимальные нейроны (в смысле, изложенном в главе 3), при этом, особенно с ростом n, приходится прибегать к помощи вычислительной техники.

Пример 5.1. Дана формула Φ = (а₂ ∨ a₃).

Вероятностная диаграмма формулы Φ имеет вид:

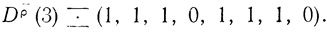
Система неравенств (5.3) для этого случая переписывается следующим образом:

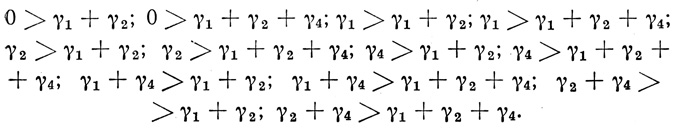
После сокращения получаем:

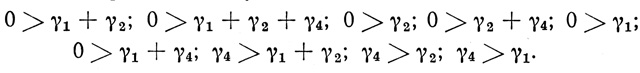
Найденная система непротиворечива. Следовательно, формулу (a₂∨a₃) можно реализовать на одном пороговом элементе с тремя входами. Возьмем δ₃ = - 1, δ₂ = - 1, δ₁ = 0, соответствующий пороговый элемент приведен на рис. 5.1, Θ = - 1.

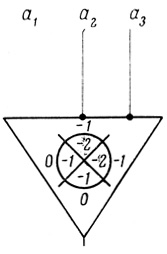
Рис. 5.1

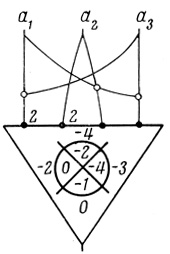
Рис. 5.2

Пример 5.2. Формула Φ ( а₁ & а₂ а₃)∨ ( ф₁ & а₂ & а₃)), вероятностная диаграмма которой D^ρ̄ (3) (1, 1, 1, 0, 1, 1, 0, 1), не может быть реализована на одном пороговом элементе в силу того, что система неравенств

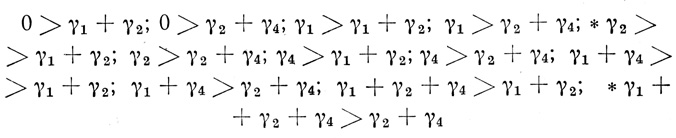
противоречива (звездочкой отмечены два противоречивых неравенства).

Остановимся на реализации данной формулы Φ на одном формальном нейроне. Система (5.4) переписывается в виде

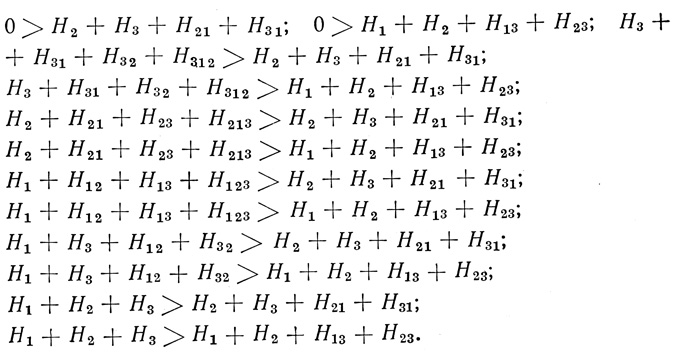
После сокращения получаем

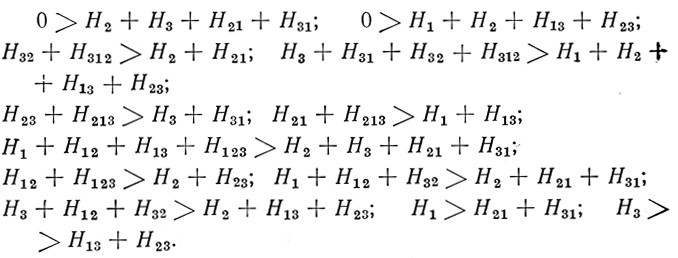
Выберем решение H₂ = - 2, H₁₃ = - 2, H₂₁ = H₃₁ = - 1, Н₁ = H₃ = H₁₂ = H₂₃ = H₃₂ = H₁₂₃ = H₂₁₃ = H₃₁₂ = 0; соответствующий нейрон показан на рис. 5.2. Формула (( a₁ & а₂ & а₃) ∨ (а₁ & а₂ & а₃)) реализуется на построенном нейроне при Θ = - 3.

Описанный метод построения нейрона по идеальной вероятностной диаграмме D^ρ̄ без каких бы то ни было изменений пригоден и для случая синтеза по точечной диаграмме D^τ. Для этого нужно точ-ки представить единицами, а пустые ячейки - нулями.

Используя указанные способы, нетрудно убедиться, что при n = 2 все 16 неэквивалентных между собой СДНФ, в которые входят только две графически различные переменные, можно разбить на две группы. В первую входит 14 СДНФ, каждую из которых можно реализовать на одном пороговом элементе. Во вторую - две: ((а & b) ∨ ( а & b)); ((а & b)∨( а & b), каждую из которых нельзя реализовать на одном пороговом элементе, но можно на одном формальном нейроне.

С увеличением n число всех F неэквивалентных между собой СДНФ, которые состоят только из n графически различных переменных, быстро возрастает. Так, уже при n = 3 из общего числа 256 СДНФ только 104 можно реализовать на одном пороговом элементе; остальные 152 могут быть реализованы либо на одном формальном нейроне, либо требуют для своей реализации построения более или менее сложной сети пороговых элементов. С дальнейшим ростом числа входов n количество функций, реализуемых одним формальным нейроном, но не реализуемых одним пороговым эле-ментом, резко возрастает, так что уже при n = 6 количество СДНФ первой группы (т. е. реализуемых на одном пороговом элементе) составляет примерно 10^-12 часть от второй группы (табл. 5.1).

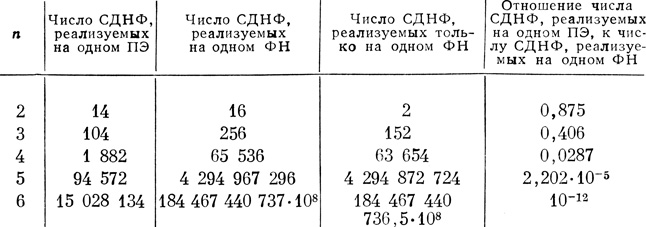
Таблица 5.1

Таким образом, формальный нейрон является более универсальным элементом по сравнению с пороговым элементом. Для любой формулы Φ исчисления высказываний можно построить формальный нейрон, на котором она реализуется. Но не для любой формулы Φ можно спроектировать пороговый элемент, на котором реализуется эта формула Φ. Кроме того, в связи с возможностью выполнять надежные вычисления при флуктуациях порогов формальный нейрон является более гибким элементом для построения схем, более надежных, нежели составляющие их компоненты.