1.4. Примеры математических моделей
Теория математических моделей является предметом специального курса и требует от читателя в первую очередь знакомства с той областью знаний, которой принадлежит моделируемый объект.
В настоящей книге приводятся традиционные примеры, иллюстрирующие применение метода математического моделирования в задачах экономического содержания.
Задача о рационе. По заданному ассортименту продуктов, при известном содержании в каждом из них питательных веществ и известной стоимости продуктов, составить рацион, удовлетворяющий необходимым потребностям, с минимальными денежными затратами.
Пусть имеется n различных продуктов и m питательных веществ (например, жиров, белков, углеводов, витаминов и др.). Обозначим через aij содержание, (в весовых единицах) j-го питательного вещества в единице веса i-го продукта; через bj обозначим минимальную (в весовых единицах) суточную потребность в j-м питательном веществе. Наконец, через xi обозначим искомое суточное потребление i-го продукта. Очевидно, что xi≥0.
Величина 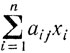 есть общее содержание j-го питательного вещества в рационе, которое не должно быть меньше минимальной потребности bj:
есть общее содержание j-го питательного вещества в рационе, которое не должно быть меньше минимальной потребности bj:
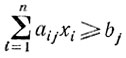
(j = 1, 2, ..., m).
Если ci - стоимость единицы веса i-го продукта, то стоимость всего рациона определяет линейная форма
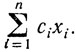
Итак, математическая формулировка задачи выбора рациона состоит в следующем:
найти
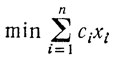
при условиях
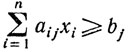
(j = 1, 2, ..., m), xi≥0 (i= 1, 2, ..., n).
Эта задача является одной из типичных задач линейного программирования.
В постановке задачи вовсе не обязательно было указывать, что это задача о рационе. Достаточно ясно, что таким же образом могут быть сформулированы многочисленные задачи об оптимальных смесях (слово "смесь" здесь следует понимать в обобщенном смысле: это и собственно смесь, и сплав, и рацион, и т. д.).
Другим типичным примером задачи линейного программирования является транспортная задача. Требуется составить план перевозок однородного груза таким образом, чтобы общая стоимость перевозок была минимальной.
Исходная информация:
- ai - количество единиц груза в i-м пункте отправления (i = 1, 2, ..., m);
- bj - потребность в j-м пункте назначения (j = 1, 2,..., n) (в единицах груза);
- cij - стоимость перевозки единицы груза из i-го пункта в j-й.
Обозначим через xij планируемое количество единиц груза для перевозки из i-го пункта в j-й.
В принятых обозначениях:
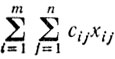 -общая (суммарная) стоимость перевозок;
-общая (суммарная) стоимость перевозок;
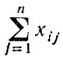 - количество груза, вывозимого из i-го пункта;
- количество груза, вывозимого из i-го пункта;
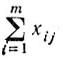 - количество груза, доставляемого в j-й пункт.
- количество груза, доставляемого в j-й пункт.
В простейшем случае должны выполняться следующие очевидные условия:
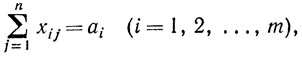
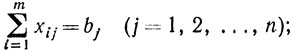
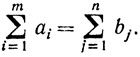
Таким образом, математической формулировкой транспортной задачи будет:
найти
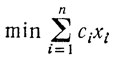
при условиях
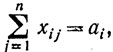
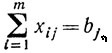
xij≥0 (i = 1, 2, ..., m; j = 1, 2, ..., n).
Эта задача носит название замкнутой транспортной модели.
Заметим, что условие
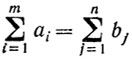
является естественным условием разрешимости замкнутой транспортной задачи.
Более общей транспортной задачей является так называемая открытая транспортная модель:
найти
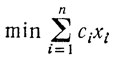
при условиях
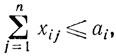
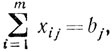
xij≥0
Ясно, что в этой задаче не предполагается, что весь груз, накопленный в i-м пункте, должен быть вывезен.
В схему транспортной задачи укладываются и некоторые другие задачи технико-экономического содержания, например, так называемая "задача о выборе": задача о наиболее экономном (в смысле суммарных затрат времени) распределении n работ между n исполнителями при известном времени, затрачиваемом каждым исполнителем на каждой работе. Эта задача является частной моделью замкнутой транспортной задачи при m = n и всех аi = bj = 1.
Заметим, что решения транспортных задач обладают свойствами целочисленности, и поэтому эти задачи относят к задачам линейного программирования, в которых целочисленность является необходимым дополнительным условием.
Задача о режиме работы энергосистемы. В качестве примера задачи выпуклого программирования рассмотрим простейшую среди задач об оптимальном ведении режима работы энергосистемы.
Рассматривается изолированная энергосистема, состоящая из теплоэлектростанций, связанных линиями передач с узлом, в котором" сосредоточена нагрузка. Ставится задача распределения активных мощностей между электростанциями в заданный момент времени. Распределение осуществляется по критерию минимизации суммарных топливных затрат на генерацию активной мощности.
Обозначим через xi активную мощность, генерируемую на i-й станции. Мощности xi заключены в пределах αi и βi, определяемых техническими условиями: αi≤x≤βi. Кроме того, должно соблюдаться условие баланса мощностей, то есть генерируемая общая мощность должна соответствовать потребляемой мощности Р с учетом общих потерь π в линиях передач:
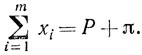
Топливные затраты на генерацию мощности xi представляют собой функцию Ti(xi), выпуклую на отрезке [αi, βi].
Таким образом, задача принимает вид:
найти
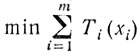
при условиях
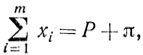
αi≤x≤βi. (i = 1, 2, ..., m).
Построенная модель является типичной задачей выпуклого программирования с линейными ограничениями. Решение этой задачи дает весьма грубое приближение к действительно оптимальному режиму работы энергосистемы. В реальной ситуации нельзя считать всю нагрузку сосредоточенной в одном узле, а следует рассматривать n узлов. Кроме того, потери в системе, естественно, не являются константой, а зависят от величин передаваемых мощностей и параметров линий передач.
В качестве следующего приближения можно рассматривать задачу, в которой я является билинейной функцией xij (i = 1, 2, ..., m; j = 1, 2, ..., n), где параметры управления xij означают количество активной мощности, передаваемое из i-й станции в j-й узел.
Очевидно, что в этой новой модели условия будут содержать нелинейности (π(xij) в уравнении баланса). Эта задача также является задачей выпуклого программирования, но более сложного типа, чем предыдущая.
Примером многоэкстремальной задачи является простейшая задача о размещении.
Даны m пунктов потребления (1, 2, ..., j, ..., m) с заданным объемом потребления bj в каждом пункте. Имеются n возможных пунктов производства (1, 2, ..., i, ..., n), причем для каждого i-го пункта известна зависимость стоимости производства fi от объема производства xi. (Предполагается, что в стоимость производства fi(xi) включены капитальные затраты.) Наконец, задана матрица транспортных расходов aij (aij - стоимость перевозки единицы продукции из i-го пункта производства в j-пункт потребления). Требуется найти такие объемы перевозок xij из i-го в j-й пункт и такие объемы производства 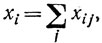 которые минимизируют суммарные расходы; иначе говоря,
которые минимизируют суммарные расходы; иначе говоря,
ищется
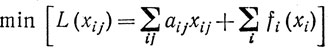
при условиях
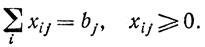
Поскольку себестоимость единицы продукции обычно убывает при увеличении объема производства, то функции fi(xi), как правило, монотонно возрастают и выпуклы вверх. Множество значений xij удовлетворяющих ограничениям задачи, образует выпуклый многогранник и, следовательно, его углы являются точками локальных минимумов функции L(xij) (рис. 1.1). Отсюда и название подобных задач - многоэкстремальные.
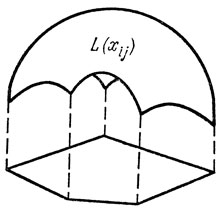
Рис. 1.1
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'