1.5. Основные обозначения

• E_n - n-мерное евклидово пространство.
• 
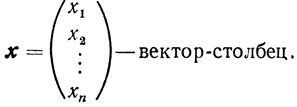
• х^Т = (x₁, x₂, ..., x_n) - вектор-строка.
• x∈R - означает, что х принадлежит R.
• x∉R - означает, что х не принадлежит R.
• R⊂S - означает, что R включено в S (теоретико-множественное включение).
• R∩S - теоретико-множественное пересечение множеств R и S.
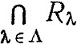• - теоретико-множественное пересечение множеств R_λ по индексу λ(λ∈Λ).
• R∪S - теоретико-множественное объединение множеств R и S.
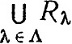• - теоретико-множественное объединение множеств R_λ по индексу λ.
• ∅ - пустое множество.
• {х: Q} - множество всех элементов x∈E_n обладающих свойством Q.
• {x∈Y: Q} - множество всех элементов x∈Y, обладающих свойством Q.
• R\S-теоретико-множественная разность, то есть множество {х: x∈R, x∉S}.
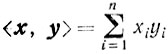• - скалярное произведение векторов x и y.
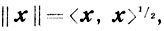• - евклидова норма вектора x.
• {x_k} - последовательность точек x_k.
• {α_k} - последовательность чисел α_k.
• А = [a_ij] - матрица размерности m*n.
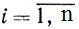• - означает, что i пробегает все целые значения от 1 до n.
• А^Т - транспозиция матрицы А: А = [a₁, a₂, ..., a_n], где
  
  
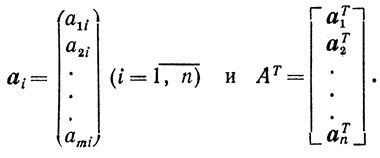
• AB - произведение матриц A и В:
  
  
• B^-1 - матрица, обратная к квадратной матрице В.
• (Ах)_i - i-я компонента вектора Ах.
• det В - определитель квадратной матрицы В.
• x≥y - полуупорядочение в E_n, означающее, что xi≥y_i ().
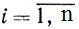• x>y означает, что x_i>y_i ().
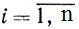• x≠y означает, что x_i≠y_i хотя бы для одного номера i.
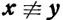• означает, что х{Фу[ ().
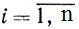• [x, y] - отрезок с концами x и y, то есть множество {z: z = αx + (1-α)y, 0≤α≤1}.
• (x, y) = {z: z = αx + (1-α)y, 0<α<1} - интервал.
• (x, y] = {z: z = αx + (1-α)y, 0≤α<1} - полуинтервал.
• [х, y) = {z: z = αx + (1-α)y, 0<α≤1} - полуинтервал.
• 
  
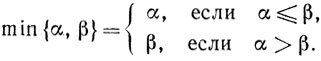
• min_x∈X φ(x) - запись задачи о минимизации скалярной функции φ(x) на множестве X.
• def - символ определения и обозначения. Например, запись y =^def f(x) + g (x) означает, что через y обозначена сумма f(x) + g(x).
• φ'(x) - градиент функции φ(х) в точке х: φ' (х) = grad φ(x).
• 
  
• 
  
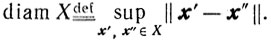
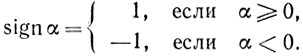
• Р {Q} - вероятность того, что выполняется свойство Q.
• Р {Q|R} - вероятность того, что выполняется свойство Q при условии R.
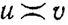• - слабая эквивалентность, означающая, что величины u и v одного порядка: и u = O(v) и v = O(u).