3.7. Задача с линейными ограничениями

Наконец обратимся к случаю, когда множество X определяется только линейными неравенствами, и покажем, что теорема Куна - Таккера будет справедлива без каких бы то ни было условий регулярности.

Пусть допустимое множество имеет вид

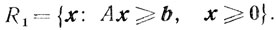(3.28)

Будем рассматривать следующую задачу выпуклого программирования:

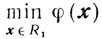(3.29)

(функция φ(х) - выпуклая).

Аналогично (3.25) и (3.26) для точки х обозначим

Напомним, что вектор s≠0 будет возможным направлением в точке x∈R₁, если существует λ₀>0 такое, что для всех λ∈[0, λ_{0] точка x + λs принадлежит R1.}

Легко видеть, что следующие неравенства являются [необходимыми и достаточными условиями того, чтобы отправление s было возможным в точке х:

Теперь можно сформулировать и доказать следующую теорему.

Теорема 3.5. Для того чтобы для выпуклой непрерывно дифференцируемой функции φ(х) существовала в R₁, оптимальная точка х^*, то есть

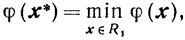
необходимо и достаточно существование такого y^*≥0, чтобы пара х^*, y^* являлась седловой точкой для функции Лагранжа L(x, y) в области x≥0, y≥0.

Доказательство. Достаточность доказана в теореме 3.1.

Необходимость. Пусть х^* оптимален. Поскольку функция φ(x) выпукла, то из теоремы 2.12 (см. замечание к теореме) следует, что

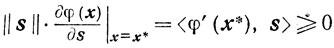(3.33)

для всех s таких, что

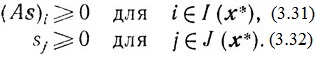
Пусть для простоты

(что не ограничивает общности). Далее воспользуемся теоремой Фаркаша. Для того чтобы использовать принятую нами в теореме Фаркаша форму записи, введем матрицу

где а_i - i-й столбец матрицы А^Т, а е_j - j-й координатный вектор. Теперь условия (3.31) и (3.32) можно записать так:

Для матрицы В и векторов φ'(х^*) и s выполняются условия теоремы Фаркаша, поэтому существует такой вектор

u^T = (y₁, y₂, .... y_k, v₁, v₂, ...., v_l)≥0,

что

то есть

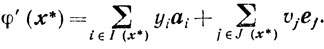
(3.35)

В теореме 3.4 доказано, что такое представление эквивалентно неравенствам Куна -Таккера (3.19)-(3.24) и, следовательно, по теореме 3.3 существует y^* такой, что х^*, y^* - седловая точка функции L(x, y) в области x≥0, y≥0.

Замечание. В этой теореме на множество R₁ не накладывались условия регулярности, в отличие от теорем 3.2 и 3.4.

В теореме Куна - Таккера для доказательства того что из оптимальности х^* следует, что пара х^*, y^* является седловой точкой функции Лагранжа L(x, y), требовалось условие регулярности Слейтера. Здесь же из оптимальности х^* сразу следует соотношение (3.35), а значит (по теореме 3.4), следуют неравенства (3.19)-(3.24), а по теореме 3.3 эти неравенства определяют седловую точку функции Лагранжа L(x, y).