3.6. Случай дифференцируемости
Весьма важными для практического использования являются неравенства, которые определяют условие существования седловидной точки. Ниже эти неравенства выписаны для основной задачи выпуклого программирования, когда допустимое множество X имеет вид
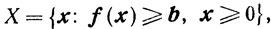
то есть когда 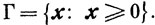
Теорема 3.3. Если функции φ(х) и f(x) основной задачи выпуклого программирования (3.2) непрерывно дифференцируемы на множестве Г = {x: x≥0}, то для того чтобы пара х*, y* была седловой точкой функции Лагранжа в области x≥0, y≥0, необходимо и достаточно выполнение условии
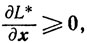 (3.19)
(3.19)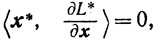 (3.20)
(3.20)x*≥0,(3.21)
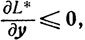 (3.22)
(3.22)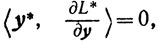 (3.23)
(3.23)y*≥0,(3.24)
где
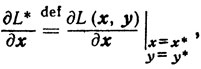
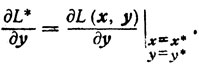
Доказательство. Запишем условия (3.19) - (3.24) в эквивалентной форме:
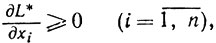 (3.19')
(3.19')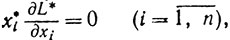 (3.20')
(3.20')x*i≥0 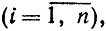 (3.21')
(3.21')
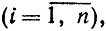 (3.21')
(3.21')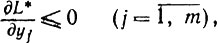 (3.22')
(3.22')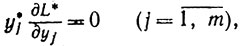 (3.23')
(3.23')y*j≥0 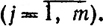 (3.24')
(3.24')
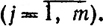 (3.24')
(3.24')Необходимость. Пусть существуют х* ≥ 0, y* ≥ 0 такие, что
L (x*, y)≤L (x*, y*)≤L (x, y*), x≥0, y≥0. (3.6)
Отсюда, в частности, следует
L (xi, y*) =def L (x1*,..., xi-1*, xi*, xi+1*, ..., xn*, y*)≥L (x*, y*)
для xi≥0, то есть точка xi* является точкой минимума функции одного переменного L(xi, y*) для xi≥0 (в частности, точкой локального минимума). А условия (3.19') - (3.21') и суть необходимые условия локального минимума при xi≥0 для функции одного переменного (поскольку либо xi* - внутренняя точка полуоси xi≥0 и тогда 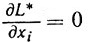 , либо xi* = 0 и тогда
, либо xi* = 0 и тогда 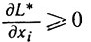 ).
).
Поскольку L(х*, y) линейна (по y), то необходимость условий (3.22) - (3.24) очевидна.
Достаточность. Пусть выполняются условия (3.19') -(3.24'). Так как φ(x) и h(x) (см. (3.4)) выпуклы, то L(x, y*) выпукла по х для x≥0 и, следовательно, для нее имеет место неравенство (см. (2.18))
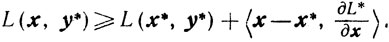
Отсюда и из (3.19) -(3.21) получаем
L(x*, y*)≤L(x, y*), х≥0.
Левое неравенство в (3.6) с очевидностью получается из линейности L(x*, y) по y и из (3.22)-(3.24).
Замечание 1. Если потребовать, чтобы множество X удовлетворяло условиям регулярности, то (3.19)- (3.24) будут необходимыми и достаточными условиями существования оптимальной точки х*.
Замечание 2. Если в задаче (3.1) Γ = En, то аналогичными рассуждениями нетрудно убедиться, что седловая точка будет определяться условием 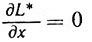 и соотношениями (3.22) - (3.24).
и соотношениями (3.22) - (3.24).
Условия (3.19) - (3.24) можно записать в иной, более геометричной форме.
Как и прежде, будем обозначать
grad φ (х) =def φ' (х), grad fi(х) =def fi'(x).
Векторы -φ'(х) и -fi'(x) в дальнейшем будем называть антиградиентами функций φ(x) и fi(x).
Заметим, что вектор -ei является внешней нормалью относительно X к граничной гиперплоскости xi = 0, а вектор -f'i(x) - внешней нормалью в точке х к граничной поверхности fi(x) = bi.
Рассмотрим точку x∈Х. Если эта точка принадлежит границе множества X, то, естественно, некоторые из неравенств, определяющих X, обращаются в равенства.
Пусть
I(x) = {i: fi(x) = bi},(3.25)
J(x) = {j: хj = 0}. (3.26)
Теорема 3.4. Пусть множество X основной задачи выпуклого программирования обладает свойством регулярности (3.3), а функции φ(x) и f(х) непрерывно дифференцируемы на множестве Г = {х: x≥0}. Тогда для оптимальности х*∈Х необходимо и достаточно, чтобы антиградиент целевой функции можно было представить в виде линейной комбинации с неотрицательными коэффициентами внешних нормалей к ограничениям в точке х*:
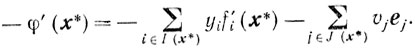 (3.27)
(3.27)Доказательство. Покажем, что условия (3.19)-(3.22) можно записать в форме (3.27). Этим и будет доказана теорема.
Условия (3.21) и (3.22) определяют, что x*∈Х. Обозначим
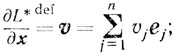
тогда (3.19) примет вид
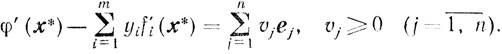
Из условия (3.24) следует yi≥0 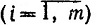 , а условия (3.20') и (3.23') примут вид
, а условия (3.20') и (3.23') примут вид
υixi* = 0 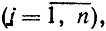
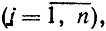
yi(bi - fi(x*)) = 0 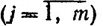
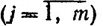
И так как х*∈Х, то в силу (3.25) и (3.26) получаем окончательно (3.27).
Из сказанного в замечании 1 следует, что условия (3.27) необходимы и достаточны для существования оптимального х*.
Замечание 3. Если в задаче (3.1) Г = Еn, то, опираясь на замечание 2, легко убедиться, что соотношение (3.27) примет вид
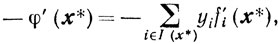 , yi ≥ 0, i∈I(x*).
, yi ≥ 0, i∈I(x*).
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'