4.9. Канонический вид задачи линейного программирования

Задачу

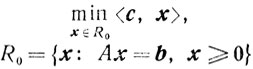(4.22)

будем называть задачей линейного программирования в каноническом виде.

Эта задача представляет собой частный случай (когда I₁=∅ и J₂ = ∅) задачи со смешанными ограничениями (4.18), и, следовательно, все доказанные теоремы и утверждения остаются в силе и для канонической задачи.

Приведение основной задачи к каноническому виду осуществляется путем введения дополнительных переменных:

для основной задачи

эквивалентной ей канонической задачей будет

(эквивалентность здесь понимается так же, как и в задачах со смешанными ограничениями).

Если заметить, что двойственной к обеим задачам будет задача

то есть задача (4.19), то доказательство эквивалентности становится тривиальным.

В дальнейшем относительно канонической задачи будем всегда предполагать m < n. Это предположение несколько упрощает изложение. С другой стороны, в реальных ситуациях всегда вводят дополнительные переменные - так называемый искусственный базис, - увеличивая тем самым число переменных задачи с n до n+m.

Для дальнейших рассмотрений понадобится ввести понятие невырожденной угловой точки множества R₀.

Определение. Угловую точку множества R₀ будем называть невырожденной, если матрица ее базиса имеет размерность m×m. Таким образом, у невырожденной угловой точки х число положительных компонент равно m. Если для простоты будем считать, что для угловой точки х положительными будут первые m компонент, то матрицей базиса этой невырожденной угловой точки будет

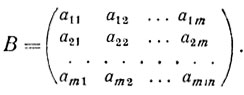
Если, как и прежде, мы запишем угловую точку х в следующем виде:

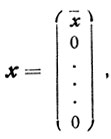
где

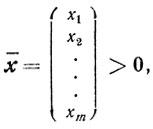
то

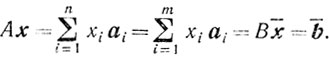
Пример. Пусть множество R₀ задается в виде

Таким образом, R₀ есть отрезок, соединяющий точки

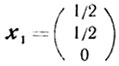
и

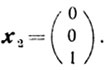
Обе они будут угловыми, но невырожденной из них является лишь первая, то есть x₁.