4.8. Приведение задач со смешанными ограничениями к эквивалентным задачам основного вида

Запишем задачи (4.18) и (4.19) в следующей форме: min[+.],

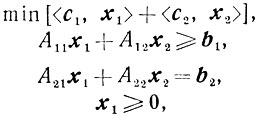(4.18)

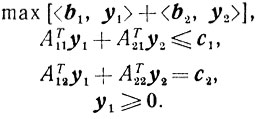(4.19)

Обозначения x₁, x₂, c₁, c₂, b₁, b₂, A₁₁,..... т. д. естественны; например, x₁-вектор, составленный из тех компонент x_j вектора х, для которых j∈J₁; этому х₁ соответствует с₁ и т. д.

Понятны и обозначения клеток матрицы

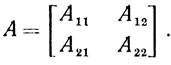
Для приведения будем каждое равенство (например, φ=0) заменять двумя неравенствами (φ≥0 и -φ≥0 или φ≤0 и -φ≤0), а вместо переменной u, на которую не наложены условия не отрицательности, будем вводить неотрицательные переменные ū и ū̄ следующим образом: u=ū-ū̄, где

Итак, сделаем следующие замены переменных:

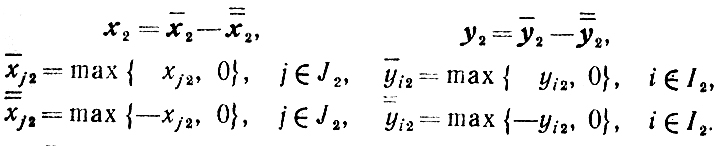
Вводя эти переменные и заменяя равенства соответствующими системами неравенств, приведем задачи (4.18) и (4.19) к следующему виду:

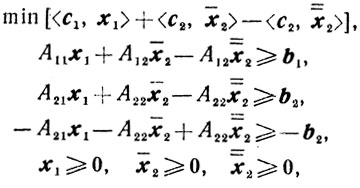(4.20)

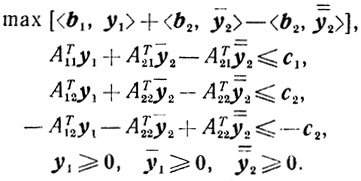(4.21)

Ясно, что (4.20) и (4.21) образуют двойственную пару задач линейного программирования основного вида.

Нетрудно убедиться, что задачи (4.18) и (4.19) эквивалентны задачам (4.20) и (4.21), а именно;

Если

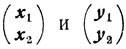
оптимальны для (4.18) и (4.19), то

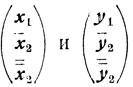
оптимальны для (4.20) и (4.21), и обратно.

2) Если допустимое множество для (4.18) пусто, то пусто допустимое множество для (4.20), и обратно.

3) Если целевая функция задачи (4.18) неограничена снизу на допустимом множестве, то неограничена снизу и целевая функция задачи (4.20), и обратно.

Утверждения 1) - 3) обосновываются элементарными рассуждениями, которые (в случае необходимости) читатель может провести самостоятельно.

Из эквивалентности этих задач вытекает, что все теоремы, доказанные для задач (4.20) и (4.21), остаются справедливыми и для задач (4.18) и (4.19).