5.1. Симплексный метод

(Симплексный метод часто называют "методом последователь-юго улучшения плана". )

По существу, симплексный метод представляет собой последовательный перебор угловых точек, при котором значение целевой функции убывает от итерации к итерации (от одной угловой точки - к другой).

Будем рассматривать каноническую задачу линейного программирования

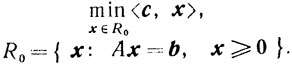(5.1)

Предполагается, что задача (5.1)-невырожденная, то есть не вырождена каждая угловая точка множества R₀.

Итерационный шаг метода состоит в переходе от угловой точки х к угловой точке х', при котором значение целевой функции убывает:

Пусть известна угловая точка х. Не ограничивая общности, можно считать, что базис В этой угловой точки образуют первые т столбцов матрицы А. Будем записывать матрицу А следующим образом:

где

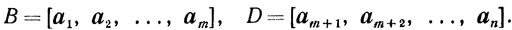
Соответствующим образом запишутся векторы х и с:

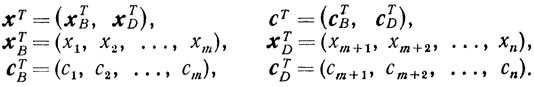
Компоненты вектора х_в иногда называют базисными, а вектора x_D-внебазисными.

Заметим, что если хоть одна компонента вектора х_в-нулевая, то угловая точка х - вырожденная. В самом деле, если, например, х_m=0, то, вычеркивая из матрицы В последние строку и столбец, получаем, что х удовлетворяет квадратной не особенной системе уравнений порядка m-1, то есть угловая точка х будет вырожденной.

Итак, известна угловая точка х. При этом.

Рассмотрим векторы

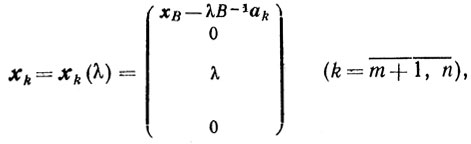(5.2)

где λ является k-й компонентой вектора х.

Во-первых, заметим, что поскольку х_в > 0, то при малых λ>0 будет х_k≥0. Далее, так как

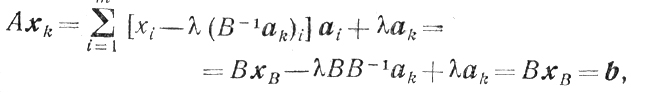(5.3)

то x_k∈R₀ при малых λ > 0. Кроме того,

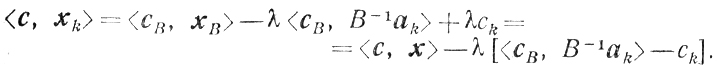
Обозначим

Заметим, что величина Δ_k определена для любого k = 1,..., n, причем при k = 1, ...., m, поскольку В^-1a_k=e_k (e_k - k-й координатный вектор), имеем

Окончательно получаем соотношение

В зависимости от знаков величин Δ_k и (В^-1a_k)_i возникают три случая.

I. Если для любого k = 1, 2, ..., n будет Δ_k≤0, то точка х - оптимальная.

Действительно, обозначим

Тогда условие Δ_k≤0 запишется так:

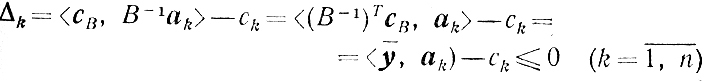
или, что то же самое,

Поскольку двойственной к задаче (5.1) является задача

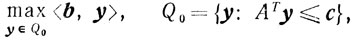(5.6)

то ȳ ∈ Q₀. И так как

то из теоремы 4.4 следует оптимальность точки х. II. Если найдется номер k≥m+1 такой, что

то множество R₀ не ограничено и функция <с, х> не ограничена снизу на R₀.

Действительно, из (5.2) следует, что при любом λ>0 будет

Отсюда и из (5.3) получаем, что x_k(λ)∈R₀. А из (5.5) следует, что

при λ→+∞.

III. Пусть найдутся такие k≥m+1 и i≤m, что

В этом случае делается итерационный шаг. Обозначим

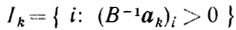
и выберем

Заметим, что λ₀ > 0, поскольку

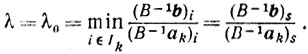
^* (Напомним, что запись (B^-1a_k)_i означает i-ю компоненту вектора В^-1а_k.)

При таком выборе величины ₀ точка х_k = х_k(λ₀) становится допустимой точкой множества R₀ (см. (5.2) и (5.3)). Номер s, для которого достигается минимум в (5.7), единствен, ввиду не вырожденности задачи (5.1). В самом деле, если бы минимум достигался более чем для одного номера, то из (5.3) видно, что вектор b выражался бы линейно с положительными коэффициентами менее чем через m векторов а_i матрицы A, то - есть точка х_k удовлетворяла бы системе уравнений размерности меньшей m и, следовательно, точка х_k была бы вырожденной угловой точкой. А это противоречит I предположению о не вырожденности. То, что х_k - угловая точка, проверить нетрудно. Для этого достаточно показать, что система векторов а₁, а,₂ ..., a_s-1, a_s+1 , ..., a_m, а_k линейно-независима. Предположим противное, то есть что найдутся такие числа β₁, β₂, ..., β_s-1, β_s+1 ,....,β_m, βk, не все равные нулю, что

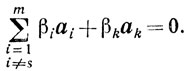(5.8)

Обозначим

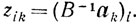(5.9)

Тогда тождество ВВ^-1ха_k-а_k≡0 запишется так:

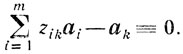
Умножая это тождество на β_k и складывая с (5.8), получаем

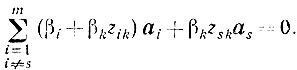
Так как det В≠0, то это равенство возможно лишь при всех нулевых коэффициентах:

Но

поскольку s∈I_k, и, следовательно, β_k = 0, а тогда и все β_i = 0, что противоречит предположению о числах β₁, β₂,.....,b_s-1, β_s+1,...,β_m, β_k.

Итак, х_k - новая угловая точка, причем

"Из изложенного выше следует, что итерационный шаг симплексного метода состоит в таком переходе от базиса а₁, а₂, ..., a_s-1, a_s, а_s+1, ..., а_m к базису а₁, а₂, ..., a_s-1, а_s+1, ..., а_m при котором целевая функция убывает, а значит, симплексный метод приводит к угловой точке x^*, в которой достигается минимум, за конечное число итераций.