7.7. О выборе параметров регуляризации

Условие (7.14) допускает приближенное определение точки минимума (если она существует) функции Ψ_αβε(x). Заметим, что если y_αβε является точкой минимума, то

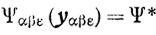
и

Так как в реальных ситуациях величина ε часто бывает не улучшаемой (не уменьшаемой), то она определяет и ту точность, выше которой вычислять точку минимума не имеет смысла (см. (7.14), (7.15)). Величина ε лимитирует также и выбор параметра β = β(ε). Условие

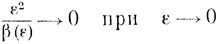
говорит о целесообразности выбора величины β(ε) того же порядка, что и .

В процессе регуляризации возникает целый ряд трудностей. Рассмотрим лишь одну из них, а именно, вопрос о выборе α₀ и β₀-начальных значений параметров регуляризации. Будем предполагать ε достаточно малой величиной. Поскольку процесс регуляризации может сходиться очень медленно (см. замечание к теореме 7.2), то выбор сравнительно большой величины α₀ может оказаться весьма невыгодным с точки зрения общих затрат времени на получение достаточно хорошего приближения к нормальному решению.

С другой стороны, для нахождения точки y_α0β0ε как правило, используются релаксационные методы минимизации, на скорость сходимости которых существенное влияние оказывает величина параметра сильной выпуклости минимизируемой функции Ψ_α0β0ε(x), то есть величина произведения α₀β₀. Как будет видно из дальнейшего (см. гл. 9), при убывании α₀β₀ скорость сходимости релаксационных процессов понижается. Вследствие этого выбор малых значений α₀ и β₀ опять-таки может увеличить общие затраты времени на получение необходимого приближения к нормальному решению и, кроме того, может быть не оправдан с точки зрения согласования с величиной ε.

В заключение отметим, что в этой главе рассматривались вопросы устойчивости задач математического программирования. Вместе с тем важным является также вопрос устойчивости численных методов минимизации к возможным ошибкам, возникающим в процессе счета. Анализ этого читатель может найти в последующих главах настоящей книги.