7.6. Сходимость метода регуляризации (общий случай)
Сделаем следующие предположения.
1) Множество Г выпукло и замкнуто;
2) Функция φ(х) выпукла и непрерывна на Г;
3) Функции fi(x), (i = 1,.., m) вогнуты и непрерывны на Г;
4) непрерывные на Г функции φε(x) и fε(x) принадлежат множеству Pε(φ, f);
5) G = {y∈X: φ(y) = minx∈Xφ(x)}≠∅.
Утверждение 1.Для любого х∈Х справедливо неравенство
ψε(x)≤ε2
Доказательство. Введем обозначения
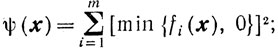
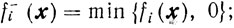
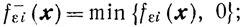
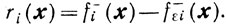
Если fi(x)≤0 и fεi(x)≤0 то
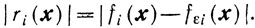
Если fi(x),≤0 а fεi(x)> 0, то
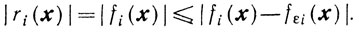
Если fi(x)>0, a fεi(x)≤0, то
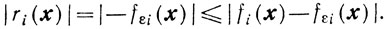
Если fi(x)>0 и fεi(x)>0, то
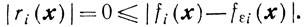
Таким образом, для любого х ∈ Г будет
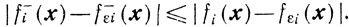
Но f-i(x)=0 при х∈Х, поэтому (см. условие 4))
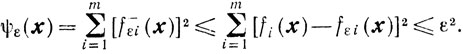
Утверждение 2. Для любого х ∈ Г справедливо неравенство
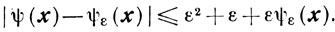
Доказательство. Обозначим
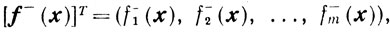
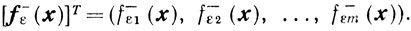
Из доказательства предыдущего утверждения следует неравенство
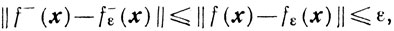
Тогда
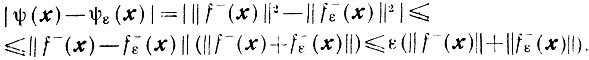
Отсюда и из неравенства
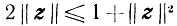
получаем
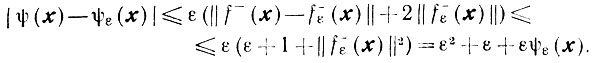
Утверждение 3. Существует
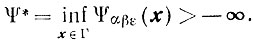
Доказательство. Так как функция
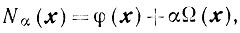
α>0
сильно выпукла на Г, то существует
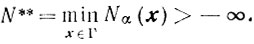
Учитывая неравенство (см. условие 4))
φε(x)≥φ(x)-ε
получаем соотношение
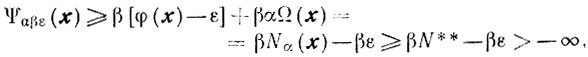
справедливое для всех х∈Г, всех 0≤β≤0<∞, 0≤ε≤ε0<0 и для любого фиксированного α > 0. Утверждение 3 доказано. Пусть, как и прежде,
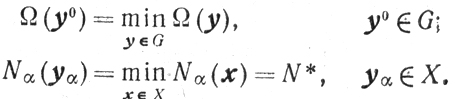
Пусть точка yαβε из Г такова, что
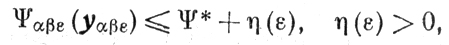 (7.14)
(7.14) и при этом
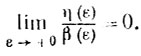 (7.15)
(7.15)Теорема 7.4. Если β=β(ε)>0 удовлетворяет условию
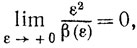
то
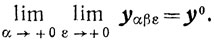
Доказательство. Из условий
ψε(x)≥0
φ(x)≤φε(x)+ε
φε(x)≤φ(x)+ε
справедливых для всех х∈Г, а также из условий
Ψαβε(yαβε)≤Ψ*+η(ε)
и
ψε(yα)≤ε2
получаем
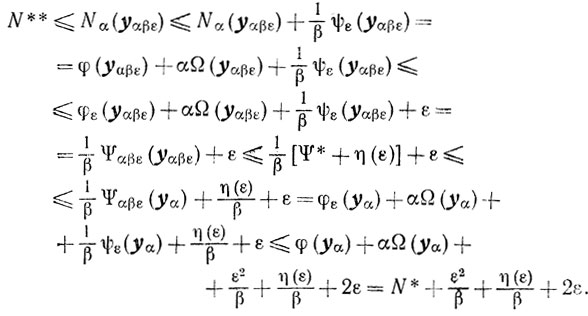
Так как
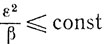
и
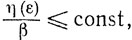
то величина
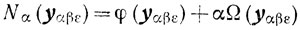
ограничена, и, поскольку функция Nα(x) сильно выпукла на Г при любом α>0, то |yαβε| - компакт (см. п. 2.13, свойство 2). Пусть ȳ-предельная точка:
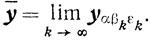
Из неравенства
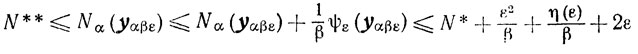 (7.16)
(7.16)следует, что
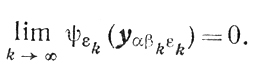
Из утверждения 2 получаем
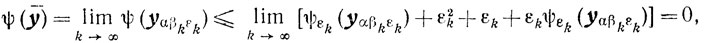
вследствие чего ȳ∈Х. Переходя к пределу в (7.16) при ε = εк→+0 получаем
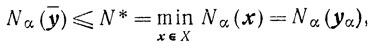
а значит,
Nα(ȳ) = Nα(yα).
Из единственности точки минимума yα сильно выпуклой функции Nα(x) следует
ȳ=yα.
Итак, любая предельная при ε→0 точка компакта {yαβε} есть у и значит,
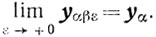
Из теоремы 7.2 следует, что
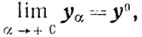
поэтому
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'