8.2. Методы с однократным вычислением значения функции
Часто в вычислительных процедурах существенные трудности возникают в связи с вычислениями значений функций φ(х), например, если значения φ(х) получают в результате того или иного эксперимента либо если φ(х) задается аналитически, но достаточно сложной для вычислений формулой. К методам, в которых при ограничениях на количество вычислений значений φ(х) достигается в определенном смысле наилучшая точность, относятся методы Фибоначчи и золотого сечения.
Эти методы, состоящие в построении последовательности отрезков [ak, bk], стягивающихся к точке х* минимума функции φ(x) на исходном отрезке [а0, b0], обладают следующими свойствами.
А. Для любого k = 0, 1, ... k-м приближением xk точки х* является одна из двух точек: yk либо zk, отстоящих на одинаковых расстояниях
yk-ak-1=bk-1-zk
от соответствующих концов отрезка [ak-1, bk-1]. Для этого должны выполняться следующие соотношения:
yk=ak-1+ck-1(bk-1-ak-1) (8.1)
yk=ak-1+(1-ck-1)(bk-1-ak-1) (8.2)
где число ck-1 выбирается таким, что
0≤ck-1≤1/2 (8.3)
В. На каждом шаге (за исключением первого) допускается вычисление лишь одного значения функции φ(х).
Пользуясь формулами (8.1)-(8.3), будем находить отрезок [ak, bk] следующим образом.
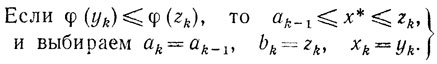 (8.4)
(8.4)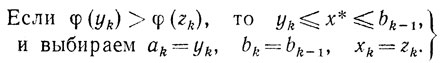 (8.5)
(8.5)Анализ процедуры (8.1)-(8.5). Из (8.1), (8.2) следует, что
yk-ak-1=bk-1-zk (8.6)
Отсюда и из (8.4), (8.5) и (8.1) получаем
bk-ak=zk-ak-1=bk-1-yk=(1-ck-1)(bk-1-ak-1) (8.7)
Обращаясь к (8.4) и (8.5), мы видим, что
xk∈[ak, bk] и φ(xk) = min{φ(yk), φ(zk)}
Теперь, в соответствии со свойством В, потребуем, чтобы на каждом шаге (за исключением первого, когда необходимы два вычисления) вычислялось одно значение функции φ (х). Возникает соотношение
 (8.8)
(8.8)Для того чтобы обеспечить выполнение условий (8.8),
необходимо соответствующим образом подбирать числа ck.
Пуст φ(yk)≤φ(zk). Тогда (см. (8.4), (8.1) и (8.7))
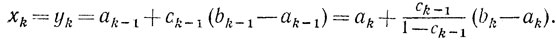
Если
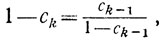
то есть
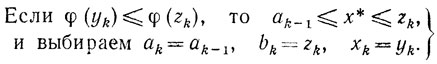 (8.9)
(8.9)то (см. (8.2))
xk=zk+1
Если
φ(yk)>φ(zk)
то (см. (8.5), (8.2), (8.1), (8.9))
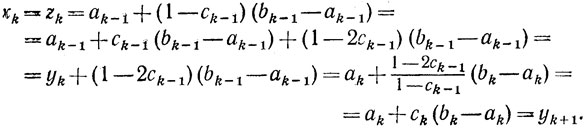
Таким образом, соотношения (8.9)обеспечивают выполнение условия (8.8)
Из (8.9) получаем
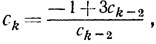 (8.10)
(8.10)и, далее, из индуктивных предположений следует
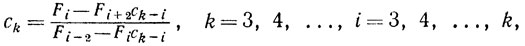 (8.11)
(8.11)где
Fj=Fj-1+Fj-2, j=3, 4,.. (8.12)
Числа Fj, удовлетворяющие соотношению (8.12) и условию F1 = F2 = 1, называются числами Фибоначчи. Приведем несколько первых из них:
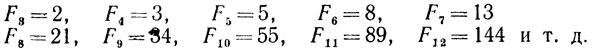
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'