8.3. Метод Фибоначчи
Будем выбирать числа ck из следующих соображений: при заранее заданном числе шагов n (то есть k = 1, 2, .... n) числа ck выберем такими, чтобы длина отрезка [аn, bn] была наименьшей.
Так как из (8.7)
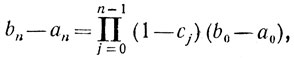 (8.13)
(8.13)то возникает задача
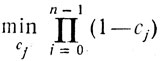 (8.14)
(8.14)при условиях
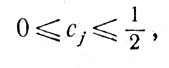 (8.3)
(8.3)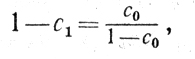 (8.15)
(8.15)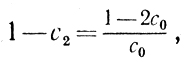 (8.16)
(8.16)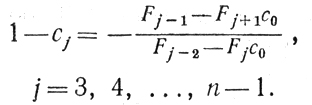 (8.17)
(8.17)Условия (8.15) -(8.17) с очевидностью вытекают из (8.9)-(8.11).
Из (8.14), (8.15), (8.16) и (8.17) следует
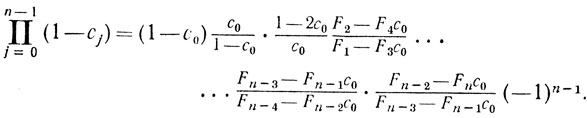
Таким образом,
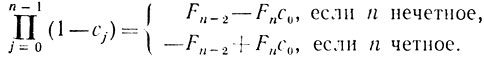 (8.18)
(8.18)Пользуясь индуктивным предположением, легко проверить, что из условия 0≤ck≤1/2, k = 0, l, ..., и из соотношения
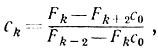
k = 3, 4,...., n,
следует для k≥3
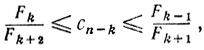
если k четное,
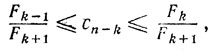
если k нечетное,
и 0≤cn-1≤1/2, 1/3≤cn-2≤1/2.
Тогда задача (8.14), (8.3), (8.15),-(8.16), (8.17) сведется к следующим двум.
Если n-нечетное, то для n≥3
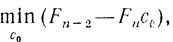
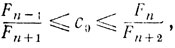
откуда
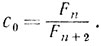 (8.19)
(8.19)Если n - четное, то для n≥4
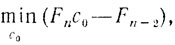
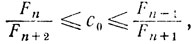
откуда
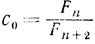
и, кроме того, с0 = 1/2 при n = 1, с0 = 1/3 при n = 2. Наконец, вычислим минимальное значение величины
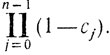
Для этого воспользуемся известным соотношением (также легко доказывается по индукции):
F2n-Fn-2Fn+2=(-1)n
Тогда из (8.18) и (8.19) вытекает, что
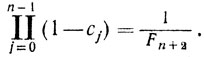
Таким образом,
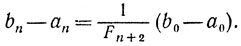 (8.20)
(8.20)Это соотношение позволяет выбрать число n при заданной точности ε > 0 вычисления точки х*. Так как
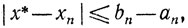
то величина n должна обеспечить выполнение неравенств
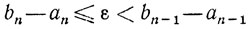
или
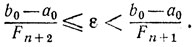
Проведенные рассмотрения можно резюмировать в виде следующей теоремы об оптимальном методе Фибоначчи (см. (8.1), (8.2), (8.9), (8.19), а также свойства A и В).
Теорема 8.1.Среди всех методов, обладающих свойствами А и В, метод Фибоначчи при заданном числе шагов n обеспечивает минимальную длину отрезка [аn, bn], содержащего точку х*.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'