8.6. Метод касательных

Этот метод может оказаться весьма эффективным для минимизации выпуклых функций.

Будем предполагать, что функция φ(х) выпукла и непрерывно дифференцируема на отрезке [а, b]. Обозначим через φ_l(х, y) следующую линейную по х функцию, определённую в точке y:

Метод состоит в следующем. Выбирают произвольную точку х₀∈[а,b] и строят функцию φ_l(x, x₀). Для вычисления точки x₁ решают следующую задачу:

при условиях

Обозначим через ξ₁, x₁ решение этой задачи. Для отыскания точки х₂ строят функцию φ_l(x, x₁) и вычисляют ξ₂, х₂-решение задачи

при условиях

Пусть вычислены точки x₁, x₂,....,x_k-1. Для того чтобы найти x_k, решают задачу

при условиях

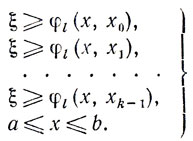(8.22)

Пусть

или, что то же самое,

Нетрудно убедиться^*, что при φ' (x_k-1) ≠ 0 задача (8,22) эквивалентна задаче отыскания такой точки х_k ∈ [а, b], что

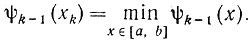(8.25)

^* (Если это вызывает затруднения, то доказательство аналогичного утверждения читатель найдет в гл. 10, п. 10.3 (раздел IV, доказательство теоремы 10.7))

Из рис. 8.1 видно, что для вычисления каждой точки х_k достаточно найти на каждом шаге две новые вершины ломаной ψ_k-1(х) (на рисунке ломаная АСВ изображает график функции ψ_k-1(х), а ломаная ADEB-график функции ψ₂(x)).

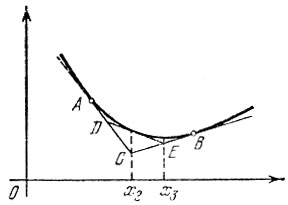
Рис. 8.1

Исследуем некоторые свойства функции ψ_k-1(x). Из выпуклости функции φ(х) следует (см. (2.18)), что

вследствие чего

для всех i=0, 1, ..., k-1 и любого x∈[a, b]. Поэтому

и, значит, ввиду (8.23) для всех х∈[а, b] справедливо неравенство

Отсюда, а также из определения функции φ_l(x, у) и соотношения (8.23) следует, что

то есть

Обоснование сходимости метода будем проводить в предположении, что φ' (x_k)≠0, k = 0, 1, .. ., поскольку в противном случае х_k является точкой минимума, и процесс на этом шаге оканчивается.

Теорема 8.2.Для выпуклой и непрерывно дифференцируемой на отрезке [а, b] функции φ(х) метод касательных сходится:

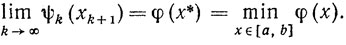
Если точка минимума х^* единственна, то

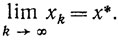
Доказательство. Из (8.25), (8.24) и (8.26) имеем

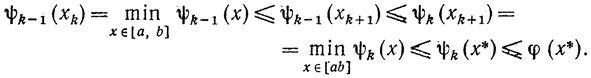
Таким образом, последовательность (ψ_k(x_k+1)} - монотонно возрастающая и ограниченная сверху, вследствие чего существует

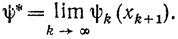
Из неравенства (8.26) следует, что

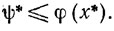(8.28)

Докажем, что ψ^* = φ (x^*). Пусть

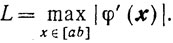
Заметим, что, ввиду выпуклости функции φ(х), будет

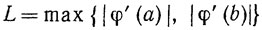
и ломаная φ_k(x) будет удовлетворять условию Липшица на отрезке [а, b] с константой Липшица L.

Так как х_k∈[а, b], k = 0, 1, ..., то существует сходящаяся подпоследовательность {x_ki}:

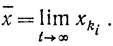
Из того что

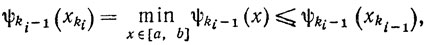
ввиду условия Липшица для функции ψ_ki-1 (х), получаем

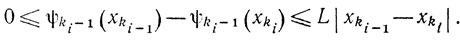
Можем считать, что индексы k₁<k₂<...<k_i<...; тогда k_i-1≤k_i-1 и, значит (см. (8.27)),

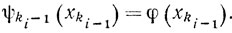
Поэтому

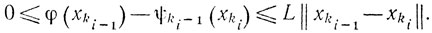
Переходя к пределу при i→∞, приходим к неравенству

откуда и следует φ(х̄) = ψ^*. Но φ(x^*)≤φ(x̄), поэтому φ(x^*)≤ψ^*. Таким образом, ввиду неравенства (8.28) будет

Первая часть теоремы доказана. Второе утверждение теоремы является очевидным следствием того, что любая предельная точка х̄ последовательности {x_k} такова, что

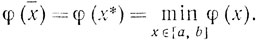
Замечание. Метод касательных применим и для одномерной минимизации выпуклых функций, свободных от требований непрерывной дифференцируемости. Поскольку, как мы видели (см. теорему 2.10), выпуклая функция φ(x) имеет в каждой внутренней точке y отрезка [а, b] левостороннюю производную φ' (y - 0) и правостороннюю производную φ'(y-0), то метод касательных может быть следующим образом приспособлен и для этого случая. В качестве линейной функции φ_l(x, x_i) будем выбирать следующую функцию:

где _i-любое число из отрезка [φ' (х_i-0), φ'(x_i+0)]. В частности, γ_i можно выбирать из условия

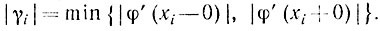
Дальнейшая конструкция метода остается прежней. Теорема о сходимости остается справедливой и в этом случае.

Схема метода. Алгоритм ищет точку минимума выпуклой и дифференцируемой функции φ(х) на отрезке [а, b] с заранее заданной точностью ε.

1-й шаг (нестандартный). Полагаем

k-й шаг (k ≥ 1). Если

то точность достигнута и процесс заканчивается. Если

то определяем абсциссу х_k точки пересечения прямых

Затем вычисляем φ'(x_k). Если φ'(x_k) = 0, то мини найден (и процесс заканчивается). Если φ' (х_k) < 0, то полагаем

Если φ' (х_k) > 0, то полагаем

и k-й шаг окончен.