8.5. Метод золотого сечения

В ряде случаев требование априорного выбора числа n создает определенные неудобства. Например, в случае, когда не лимитировано количество вычислений значений функции φ(x), а критерием окончания процедуры вместо гарантированной точности определения величины х^* (то есть длины отрезка [а_n, b_n]) является некоторой другой, скажем, точность определения величины φ(x^*). Возникает проблема построения метода, не требующего определения вначале числа я, как это необходимо в методе Фибоначчи, и вместе с тем такого, точность которого (в смысле длины отрезка [а_n, b_n]) была бы не намного хуже точности метода Фибоначчи. Таким методом является так называемый метод золотого сечения, обладающий еще одним достоинством: его вычислительная схема укладывается в схему метода Фибоначчи. При этом первый этап - определение числа n и величины F_n/F_n+2 здесь отсутствует.

Пусть c_k = const, k = 0, 1, ... Тогда из (8.9) следует

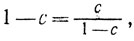
откуда

И так как 0≤c≤1/2, то

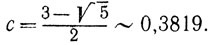(8.21)

Схема метода очевидным образом упрощается по сравнению с предыдущей.

Поясним название метода. Как известно, точка y_k осуществляет золотое сечение отрезка [a_k-1, b_k-1], если

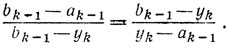
Справедливость этого соотношения очевидна из (8.7) и условия

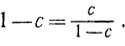
Наконец, сравним точность методов Фибоначчи и золотого сечения.

Из (8.13) и (8.21) получаем

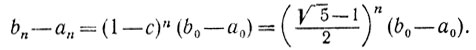
Из формулы Бине^*

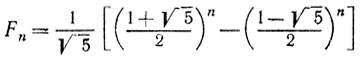
^* (Элементарное доказательство можно найти в [3]. )

следует, что для больших n

Тогда

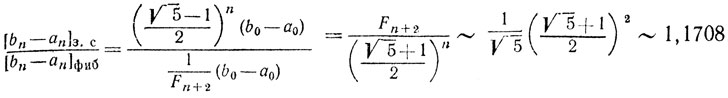
Таким образом, длина отрезка [a_n, b_n]_з.с построенного методом золотого сечения, на 17% больше длины отрезка [а_n, b_n]_фиб., построенного по методу Фибоначчи.

Заметим, что для достаточно больших n будет

то есть и метод Фибоначчи, и метод золотого сечения при больших п начинаются практически в одной и той же точке с₀.

Заметим, что уже

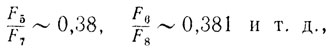
поэтому иногда можно комбинировать оба метода: первые шаги делать по методу золотого сечения, а затем, когда оптимум достаточно близок, зафиксировать число n и переходить к методу Фибоначчи.