9.2. Понятие о релаксационном процессе. Леммы
Рассматривается задача минимизации выпуклой дифференцируемой функции φ(x) на выпуклом замкнутом множестве X:
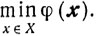
Процесс построения последовательности точек {xk} будем называть релаксационным, если
xk∈X и φ(xk+1)≤φ(xk), (k = 0, 1, ...).
Всюду дальше будем предполагать, что множество
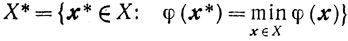
не пусто.
При выводе оценок скорости сходимости релаксационных процессов будем также предполагать, что
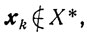
так как в противном случае
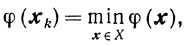
и релаксационный процесс оканчивается.
Оценки сходимости всех рассматриваемых ниже методов опираются на три леммы.
Лемма 9.1.Если числовая последовательность {μk} такова, что
μk-μk+1≥τkμk2, μ>0, τk≥0, (k=0, 1,...)*
то
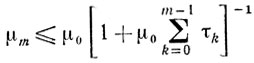
(m=1,2, ...).
Доказательство. Из условий леммы следует, что
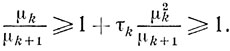
Ввиду этого
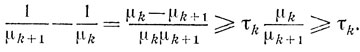
Суммируя это неравенство по k, получим
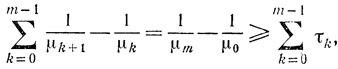
откуда и следует искомая оценка.
Лемма 9.2. Если числовая последовательность {μk} такова, что
μk-μk+1≥τkμk2, μ>0, τk≥0, (k=0, 1,...)
то
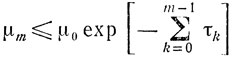
(m=1, 2,....)
Доказательство с очевидностью следует из условия μk > 0, поскольку 0<1-τk≤1 и, следовательно,
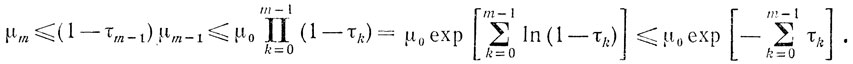
* (Здесь μ2k означает квадрат числа μk.)
Лемма 9.3.Если φ(x) ∈ С1,1 (X), то есть существует такая константа L > 0, что для любых х, y ∈ X выполняется неравенство
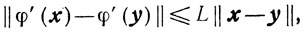
то для любых х, y ∈ X будет
φ(x)-φ(y)≥<φ'(x), x-y>-L/2||x-y||2
Доказательство. Используя условие φ (x) ∈ C1,1(Х) и неравенство Коши - Буняковского, получим
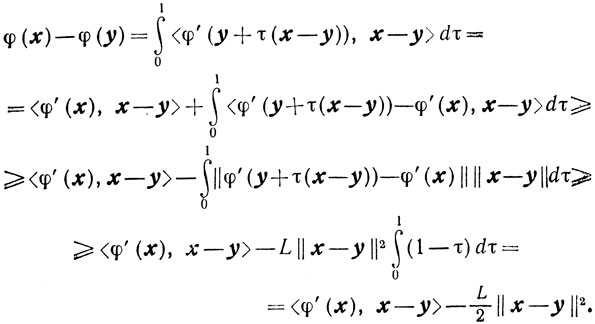
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'