9.3. Теоремы об оценках
Обозначим
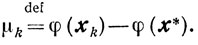
Из выпуклости функции φ (x) следует соотношение
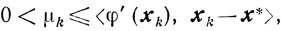 (9.1)
(9.1)справедливое для всех точек xk, ввиду предположения
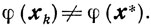
В основе большинства дальнейших исследований сходимости релаксационных методов минимизации лежит следующая элементарная теорема об оценке.
Теорема 9.1.Если
1) функция φ(x) выпукла и дифференцируема на выпуклом и замкнутом множестве X;
2) множество X* не пусто;
3) последовательность {xk} релаксационна, то имеет место оценка
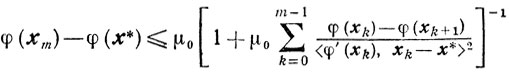 (9.2)
(9.2)Доказательство. Так как (см. (9.1))
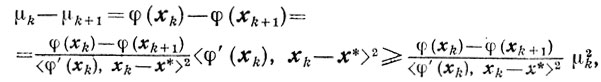
то, применяя к этому соотношению лемму 9.1, приходим к оценке (9.2). Очевидно, что если при m→∞ ряд, стоящий в правой части неравенства (9.2), расходится, то имеет место слабая сходимость (то есть φ (хm) → φ (х*)-сходимость по функционалу) релаксационного процесса. Сильная же выпуклость функции φ(х) гарантирует в этом случае (см. (2.24)) сильную сходимость процесса (то есть сходимость последовательности {xk} к решению х*). Таким образом, для исследования сходимости релаксационных процессов при помощи формулы (9.2) следует уметь оценивать снизу величину
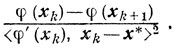
Заметим, что
<φ'(xk), xk-x*>→0 при φ(xk)→φ(x*)
Это обстоятельство для определенных классов релаксационных методов позволяет находить такую величину C > 0, не зависящую от числа итераций k, что
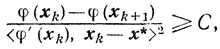
и, следовательно, получать оценки вида φ(хm)-φ(x*)≈ O(1/m). Рассмотрим теперь задачу отыскания безусловного минимума функции φ(х), то есть тот случай, когда X = Еn.
Функция φ(х) по-прежнему выпукла и дифференцируема. Очевидно, что для задач безусловной минимизации в определении релаксационной последовательности условие xk∈X становится излишним.
Теорема 9.2. Если
1) X = En;
2) выпуклая функция φ(х) дифференцируема;
3) множество Х0 = {х : φ(х) ≤ φ(х0)} ограничено: diamA:X0 = η(x0) = η < ∞;
4) последовательность {хk} релаксациопна, то справедливо неравенство
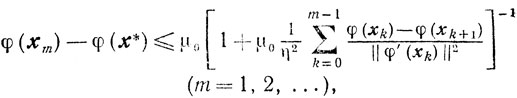 (9.3)
(9.3)где μ0=φ(x0)-φ(x*).
Доказательство есть очевидное следствие оценки (9.2), поскольку
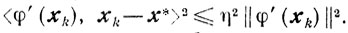
Замечание. Если существует такой номер m0, что φ(хm0) > φ(xm0+1). то из (9.3) следует неравенство
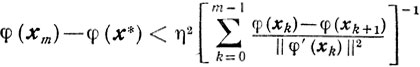
(m=m0+1, m0+2, ...). (9.4)
Теорема 9.3.Если Х=Еn, функция φ(х) сильно выпукла и дифференцируема, а последовательность {xk} релаксационна, то справедливы неравенства
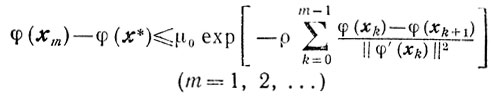 (9.5)
(9.5)и
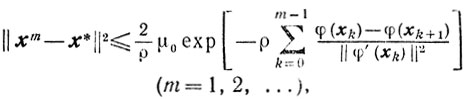 (9.6)
(9.6) (m=1,2, ...),
где ρ-параметр сильной выпуклости
Доказательство с очевидностью следует из свойств сильной выпуклости (см. (2.26)):
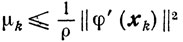
и (см. (2.24))
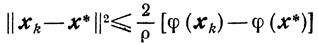
и из леммы 9.2:
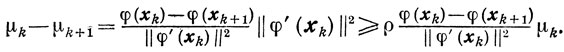
Оценки (9.4) - (9.6) позволяют в процессе вычислений накапливать информацию о скорости приближения φ(хm) к φ(x*), а в случае сильной выпуклости-о скорости приближения хm к x*. Заметим, что до тех пор, пока порядок величины
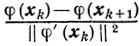
не ниже, чем О (1/k), релаксационный процесс минимизации остается сходящимся. В реальных ситуациях используют следующий прием. Задаются величиной ε>0, например, выбранной на данном этапе точностью вычислений, и продолжают процесс до тех пор, пока не нарушится неравенство
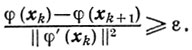
Но как только начинает устанавливаться ситуация
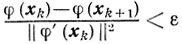
и дальнейшее применение выбранного алгоритма минимизации не сулит ее изменения, итерации останавливают. Продолжение процесса минимизации связано либо с изменением параметров алгоритма (например, с повышением точности вычислений), либо с переходом к другому, более эффективному в данном случае методу.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'