10.7. О сходимости релаксационных методов в задачах с не выпуклой целевой функцией

Рассмотрим функцию φ(х), определенную на выпуклом замкнутом множестве X. Введем обозначения:

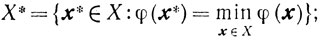
p^*(х) - проекция точки х на множество X^*:

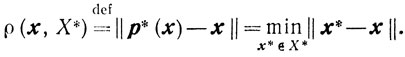
Для ε>0 определим множество

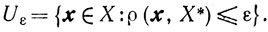
Пусть v=x-υφ'(x), υ>0, p(v)-проекция точки υ на множество X:

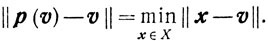
Всюду дальше будем предполагать, что выполняются следующие условия:

1) множество X выпукло и замкнуто;

2)

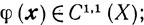
3)Х^*≠∅;

4) для всякого ε>0 найдется такое δ = δ (ε) > 0, что

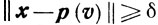
для всех

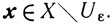
Заметим, что в любой точке локального минимума (функции φ(x) на множестве X будет

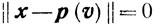
(замечание к теореме 2.16); поэтому условие 4) означает, что всюду вне множества X* не выполняются необходимые условия локального минимума.

Обратимся к анализу сходимости методов проекции градиента и условного градиента в применении к задаче

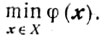
Метод проекции градиента(ср. схему 1 п. 10.2).

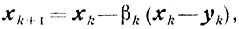
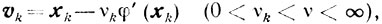
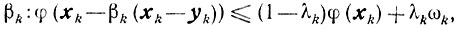
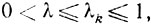
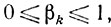
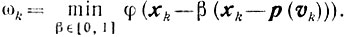
Теорема 10.12. Если выполняются условия 1)-4), то последовательность {х_k}, построенная методом проекции градиента, такова, что

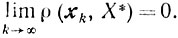
Ясли, кроле того,

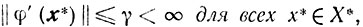
то

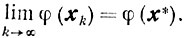
Доказательство. Из леммы 9.3, аналогично тому, как выводилось неравенство (10.33) (см. доказательство теоремы 10.3), получаем

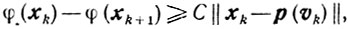
где

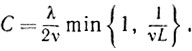
Отсюда ввиду условия 4) следует, что для любого ε>0 и всех x_k∈X\U_ε

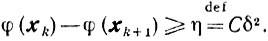
Поскольку теорема 9.12 справедлива и для задачи минимизации на выпуклом и замкнутом множестве X, то из последнего неравенства и теоремы 9.12 вытекает

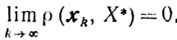
Далее, пользуясь формулой конечных приращений, поручаем

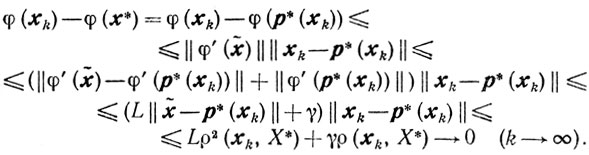
Метод условного градиента (ср. схему 4 п. 10.1).

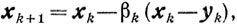
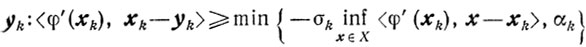
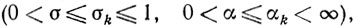
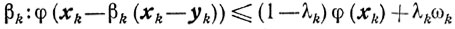
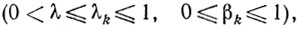
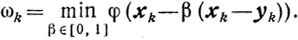
Теорема 10.13.Если выполняются условия 1)-4) и если существует такое число χ>0, что

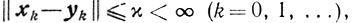
то последовательность {х_k}, построенная методом условного градиента, такова, что

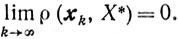
Если, кроме того,

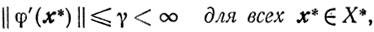
то

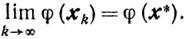
Доказательство. Если

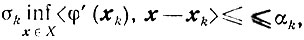
то, <φ'(x_k), x_k-y_k>≥σ_k<φ'(x_k), x_k-p(v_k)> где p(v_k)- проекция точки v_k=x_k-υ_kφ'(x_k) (0<υ_k≤υ<∞) на множество X. Но (см. (10.25))

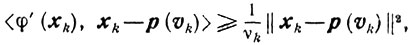
и значит,

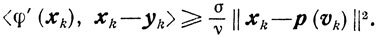
Если же

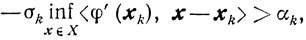
то

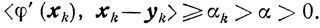
Поэтому для всех х_k∈Х\u_ε ввиду условия 4)

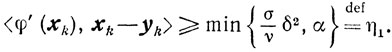
Пользуясь леммой 9.3, получаем неравенство

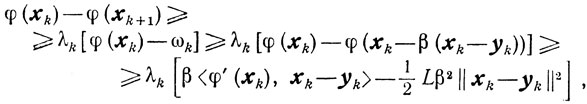
справедливое для всех β∈[0, 1]. Выберем

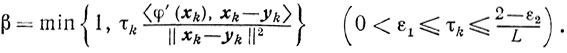
Если β = 1, то вследствие неравенства

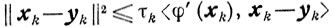
получаем

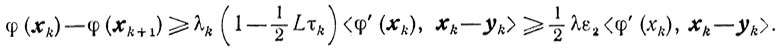
Если

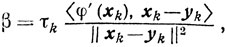
то

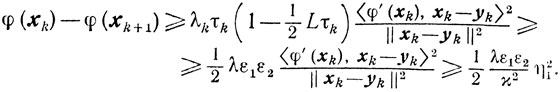
Итак,

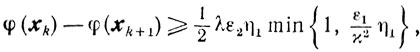
и для всех x

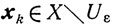
справедливо неравенство

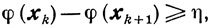
где

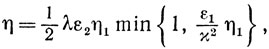
а значит, по теореме 9.12,

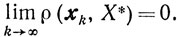
Соотношение

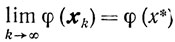
доказывается так же, как и в предыдущей теореме.

Замечание об условиях существования оценок скорости сходимости. В случае, когда для выпуклой функции φ(x) выполняются условия теорем 10.12 и 10.13, справедливы оценки скорости сходимости методов проекции градиента и условного градиента, аналогичные тем, которые приводились в пп. 10.1 и 10.2. Правда, константы в этих оценках будут иными, но порядок скорости сходимости сохраняется прежним.