10.6. Способы отыскания допустимой точки
Во всех рассмотренных релаксационных методах решения задач математического программирования предполагалась известной начальная точка х0∈Х. Ниже излагаются три способа отыскания точки х, принадлежащей множеству
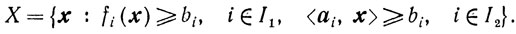
Для отыскания точки x, -удовлетворяющей линейным ограничениям <ai, x> ≥ bi, i∈I2, применим любой из методов, рассмотренных в линейном программировании (см. методы отыскания исходной угловой точки). Заметим, что эти методы конечны.
Итак будем предполагать, что нам известна точка х0∈Еn такая, что <ai, x> ≥ bi, i∈I2,. Обозначим
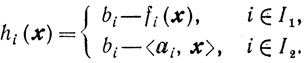
Способ 1. Пусть
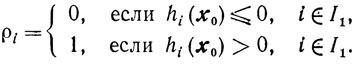
Для отыскания допустимой точки множества X будем решать следующую задачу:
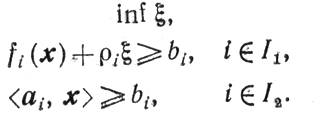 (10.64)
(10.64) Исходной допустимой парой x0, 0 для этой задачи будет
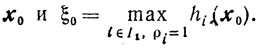
Обозначим через х*, ξ* решение задачи (10.64). Заметим, что так как ξ* = inf ξ, то такое обозначение предусматривает, вообще говоря, и случай, когда ξ* = -∞. Если для задачи (10.64) найдется такая допустимая пара x, ξ, что ξ≤0, то точка х будет принадлежать множеству X. Если же в решении х*, ξ* задачи (10.64) будет ξ*>0, то множество X пусто. В самом деле, если Х≠∅, то существует такая точка х, что hi(x)≤0 для всех i∈I1∪I2. Тогда, взяв
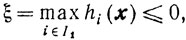
получаем, что пара х, ξ допустима и при этом справедливо неравенство ξ<ξ*, противоречащее предположению о минимальности величины ξ*.
Решать задачу (10.64) можно, применяя любой сходящийся релаксационный процесс. Причем в нашем случае достаточна слабая сходимость. В применении к задаче
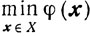
слабая сходимость означает, что
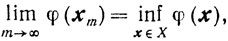
поскольку из слабой сходимости релаксационного процесса решения задачи (10.64) вытекает, что
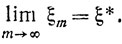
Теорема 10.10.Если множество X не пусто и облагает свойством регулярности относительно нелинейных ограничений, то любой слабо сходящийся релаксационный процесс приводит к допустимой паре x, ξ≤0 задачи (10.64) за конечное число итераций.
Доказательство. Если ξ0≤0, то х0∈Х. Предположим, что ξ0>0. Так как множество X регулярно, го найдется точка х∈Х такая, что
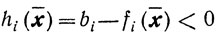
для всех i∈I1 и <ai, x̄>≥bi для всех i∈I2. Вследствие этого пара
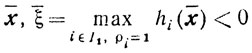
будет удовлетворять ограничениям задачи (10.64) и, значит,
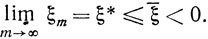
Но исходное значение ξ0 положительно (ξ0>0), поэтому из свойств сходящейся последовательности {ξm} вытекает существование такого номера m0, начиная с которого все ξm≤0 (m = m0, m0+1, ...). Таким образом, любой слабо сходящийся релаксационный процесс за конечное число m0 итераций приводит к паре xm0, ξm0≤0.
Способ 2. Пусть х0-фиксированная точка из Еn. Обозначим
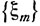
Для отыскания допустимой точки множества X будем решать следующую задачу:
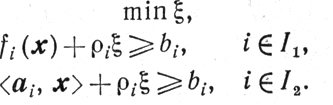 (10.65)
(10.65)Исходной допустимой парой x0, ξ0 Для этой задачи будет
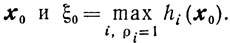
Ясно, что если найдется такая допустимая пара х, ξ, что ξ = 0, то точка х будет принадлежать множеству X. Если же в решении х*, ξ* задачи (10.65) будет *>0, то множество X пусто.
В отличие от предыдущего способа, здесь отыскание допустимой точки множества X происходит в один этап (не надо отдельно решать задачу отыскания точки, удовлетворяющей линейным ограничениям), гарантировать же конечность релаксационного процесса в способе 2 можно лишь в случае ξ*<0, например, если множество X регулярно относительно линейных и нелинейных ограничений.
Способ 3. Рассмотрим основную задачу выпуклого программирования
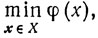
где
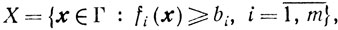
а
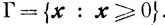
Третий способ представляет собой обобщение М-метода решения задачи линейного программирования на нелинейный (выпуклый) случай.
Определим для фиксированной точки x0≥0 величину
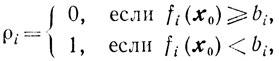
и рассмотрим задачу
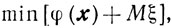
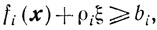
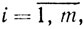
x≥0, ξ≥0
Здесь М - некоторое число, о выборе которого речь пойдет ниже. Пара
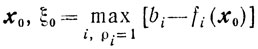
будет допустимой для задачи (10.66). Мы покажем, что при определенных условиях решение х*, ξ* этой задачи таково, что точка х* является оптимальной точкой основной задачи.
Пусть выполняются все условия, при которых справедлива теорема 3.4, а именно множество X основной задачи выпуклого программирования обладает свойством регулярности (3.3), а функции φ(х) и fi(x) (i=1,...,m) непрерывно дифференцируемы на множестве
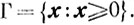
В этих предположениях справедлива следующая теорема.
Теорема 10.11. Если разрешима основная задача выпуклого программирования, то найдется такое число - М0, что для всех М≥М0 в любом решении х*, ξ* задачи (10.66) точка х* будет оптимальной для основной задачи.
Доказательство. По условию существует такая уточка x*∈Х, что
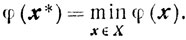
Из теоремы 3.4 следует, что найдутся y*i (i = 1,..., m) и v*j (j = 1,...,n), для которых будут выполняться соотношения
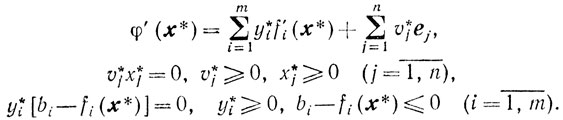 (10.67)
(10.67)Та же теорема 3.4 в применении к задаче выпуклого программирования (10.66) устанавливает необходимые и достаточные условия оптимальности пары х, ξ. А именно существование таких х, ξ, yi (i = 1,...,m), vj (j = 1,..., n+1), для которых справедливы соотношения
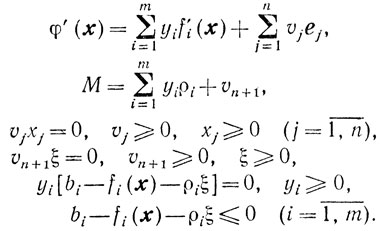 (10.68)
(10.68)Построим теперь решение этой системы, опираясь на (10.67). Выбирая
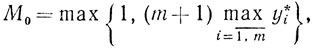
получаем
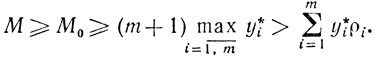
Тогда при
x = x*, ξ = ξ* = 0, yi = y*i (i = 1,...,m), vj = vj*
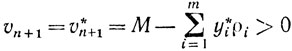
будут выполняться все соотношения системы (10.68) и, следовательно, пара х*, ξ* = 0 является решением задачи (10.66).
Покажем теперь, что при М ≥ М0 в любом решении х̄, ξ̄ задачи (10.66) будет ξ̄ = 0 и, следовательно, так как из (10.68) следует (10.67), то х оптимален для исходной задачи. Предположим, что это не так, то есть ξ̄>0. Тогда, поскольку пара х*, ξ*=0 оптимальна для задачи (10.66), то
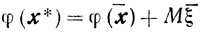
и, значит,
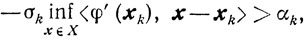 (10.69)
(10.69)Рассмотрим функцию
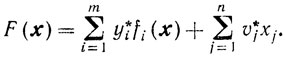
ИЗ (10.67) вытекает, что F' (х*) = φ' (х*) и
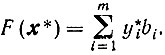
Так как v*j≥0 (j = 1,...,n) и x̄≥0, то
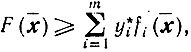
и поэтому
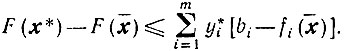 (10.70)
(10.70)Поскольку рассматривается основная задача выпуклого программирования, то все функции fi(x) вогнуты, и так как все y*i≥0, то вогнута и функция F(x), вследствие чего
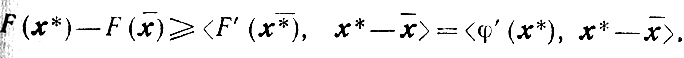
Из выпуклости функции φ(x) получаем
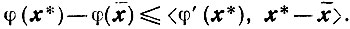
им образом, справедливо неравенство
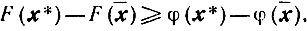 (10.71)
(10.71)Если все
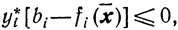
то ввиду (10.70) и (10.71) приходим к неравенству
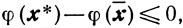
противоречащему предположению, что ξ̄>0 (см. (10.69)). Пусть
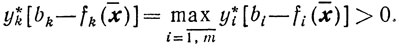
Тогда (см. (10.70)) имеем
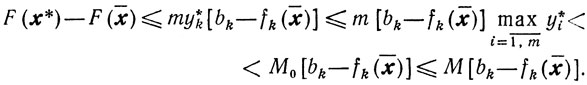
Отсюда с учетом (10.71) и (10.69) получаем
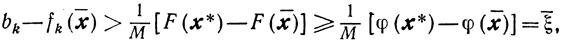
то есть
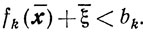
Но ведь пара x̄, ξ̄ удовлетворяет ограничениям задачи (10.66), поэтому при ρk=1 последнее неравенство противоречит допустимости пары х̄, ξ̄. И тем более оно противоречиво при ρk = 0. Итак, предположение ξ̄>0 ведет к противоречиям. Теорема доказана.
Следствие. Если найдется такое большое М, что в решении х*, ξ* М-задачи (10.66) будет ξ*>0, то основная задача выпуклого программирования неразрешима.
Действительно, если основная задача разрешима, то для М≥М0 в любом решении М-задачи будет ξ*=0. Противоречие и доказывает утверждение следствия.
Обсуждение. 1. Естественно, что величина М0 практически нам неизвестна. Ввиду этого в качестве М выбирают некоторое достаточно большое число. При этом следует иметь ввиду, что выбор слишком большого М может привести к потере точности вычислений.
2. Если в множестве X выделены линейные ограничения, то есть
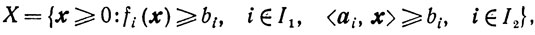
то теорема 10.10 сохраняет силу и при условии регулярности множества X относительно лишь нелинейных ограничений.
3. Наконец, укажем на одну возможность применения М-метода. Предположим, что в результате некоторого процесса минимизации получена точка х0, близкая к x*, Но не принадлежащая множеству X. В этом случае применение способа 3 может оказаться весьма перспективным для уточнения приближенного решения x0.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'