2.3. Модели и результаты

2.3.1. Коэффициент передачи и постоянная времени

Важнейшим научным достижением кибернетики является создание теории систем. Мы не можем здесь подробно изложить ее выводы, но небольшой экскурс в теорию систем, не требующий от читателя знаний сверх школьной программы, будет, с нашей точки зрения, полезным.

Нас интересует, как элемент (звено) передает поступающий к нему сигнал. В простейшем случае, когда сигнал является постоянным и не изменяется во времени, передачу его можно описать статической характеристикой самого звена. Если звено является линейным, эту характеристику можно изобразить прямой линией.

На рис. 41 изображена характеристика измерительного звена, которое реагирует на изменение длины измеряемого объектах x_вх = 1 мм изменением напряжения x_вых = 0,5 В. Предположим, что величины x_вх и x_вых (в общем виде уже объясненные на рис. 39) характеризуют отклонения от нормального состояния (рабочей точки).

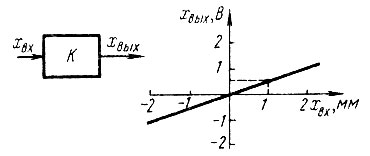
Рис. 41. Статическая характеристика П-звена (пропорционального звена)

Уравнение, описывающее передачу информации данным звеном, будет выглядеть как

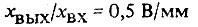
при условии, что мы измеряем x_вых в вольтах, а x_вх в миллиметрах.

Поскольку первоначально мы рассматриваем x_вых и x_вх как постоянные величины, такое уравнение мы можем назвать статическим. В общей форме оно выглядит так:

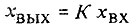
Коэффициент K статического уравнения 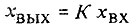(или, что то же самое, техническую характеристику линейного звена) принято называть коэффициентом передачи. Такое звено называется также пропорциональным (П-звеном), поскольку выходная величина прямо пропорциональна входной.

В нашем случае, коэффициент передачи K = 0,5 ^В/_мм.

Но нас интересует не только статическая, но и динамическая характеристика звена, и в первую очередь - явление задержки сигнала (см. рис. 35, 36), которое снижает эффективность регулирования.

Мы уже рассматривали динамическую характеристику звена в виде реакции на скачок (см. рис. 35-37). Звенья, изображенные на этих рисунках (транспортерная лента, паяльник, рычажные весы), также являются пропорциональными (П-звеньями), по крайней мере, в рамках модели.

Другое звено, с работой которого мы познакомились, это вентиль парового отопления. На рис. 37 показано, как воздействует положение вентиля (регулирующее воздействие x_вх) на температуру в комнате (x_вых). На рис. 42, а изображена скачкообразно изменяющаяся функция, а на рис. 42, б - реакция на скачок как переходная функция звена. Из переходной функции определяются:

Статическая характеристика (для постоянных значений x_вх и x_вых) с коэффициентом передачи, равным 0,4 K/%:

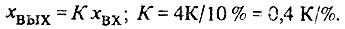
Прямое K - это кельвин - единица измерения температуры.

Динамическая (переходная) характеристика - неколебательный (апериодический) процесс, заканчивающийся через 40 мин.

Время успокоения T_5% - время, которое проходит до того, как установится новое конечное состояние (в пределах допустимых отклонений).

Время установки в данном случае сравнительно велико, что говорит о большой инерционности звена.

На рис. 42, в показана переходная функция для такого же нагревательного устройства, вентиль которого находится на большем расстоянии от радиатора. Время, которое требуется для притока пара от вентиля к радиатору, с очки зрения регулирования, является задержкой (запаздыванием) (см. 35). Статическая характеристика при этом не меняется и коэффициент передачи остается тем же. Но длительность перехода в установившееся состояние возрастает, что крайне нежелательно для регулирования. Обшивка радиаторов отопления, которую часто делают, чтобы улучшить их внешний вид, также увеличивает время успокоения. Длительность перехода зависит от определенных параметров звена. Комбинация этих параметров характеризует постоянные времени.

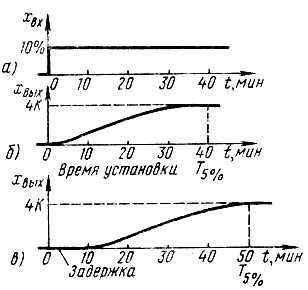
Рис. 42. Процесс установки комнатной температуры на заданном уровне: а - задающее воздействие (скачкообразно изменяющаяся функция); б - переходная функция при отсутствии задержки; конечное (стационарное) значение устанавливается за время t>T_5% ≈ 40 мин; в - переходная функция с задержкой; конечное значение достигается за время t>T_5% ≈ 50 мин

Постоянными времени называются динамические характеристики звена, от которых зависит процесс перехода, и прежде всего время успокоения.

Роль, которую играет для П-звена постоянная времени проиллюстрирована на рис. 43. Очевидно, что чем меньше постоянные времени, тем лучше, потому что при этом сигналы передаются быстрее. Уменьшение задержки сигнала позволяет решить многие проблемы регулирования.

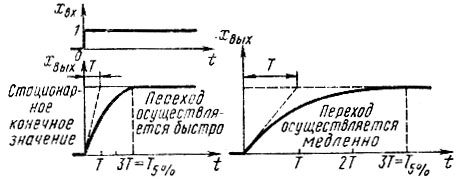
Рис. 43. Роль постоянной времени

На рис. 44 показана реакция интегрирующего звена: выходная величина равна интегралу входной величины по времени. К такого рода звеньям относятся, например, обычные моторы, у которых выходной сигнал увеличивается, пока входной сигнал отличен от нуля. Установившееся стационарное состояние (о статическом здесь речи быть не может) характеризуется в данном случае постоянной скоростью изменения x_вых, пропорциональной x_вх, которую мы принимаем за постоянную величину. Соответствующие формулы мы приводить не будем.

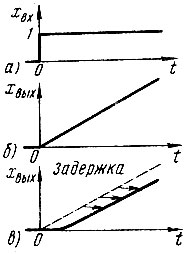
Рис. 44. Переходные функции интегрирующего звена: а - задающее воздействие (скачкообразно изменяющаяся функция); б - переходная функция без задержки (например, длина троса, сматываемого с равномерно вращающегося барабана); в - переходная функция с задержкой (например, длина троса, сматываемого с барабана, который постепенно набирает заданную скорость вращения - см. рис. 43)