2.3.2. Контур регулирования как система передающих звеньев
Мы не собираемся здесь более подробно рассматривать математический аппарат кибернетики - это было бы слишком сложной задачей, требующей обширного использования математики. Но и с теми сведениями, которыми мы располагаем, можно разобрать ряд интересных свойств регулирования.
Интерес, представляет для нас следующая проблема: мы говорили, что задержка сигнала является причиной всевозможных неприятностей. Но и в статическом режиме, когда значение сигнала не изменяется, контур регулирования также может оказаться не в состоянии выполнить свою задачу, которая, как известно, состоит в том, чтобы поддерживать регулируемую величину x равной заданному значению w, несмотря на воздействие помех.
Рассмотрим такую ситуацию на примере рис. 45. Пусть все звенья, составляющие контур регулирования, будут пропорциональными (П-звеньями), имеющими характеристику, показанную на рис. 41. Предположим, что в нормальном режиме (где точная настройка обеспечивает равенство регулируемой величины своему заданному значению) 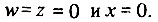
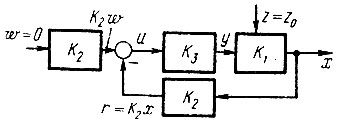
Рис. 45. Условный контур регулирования со статически пропорциональными звеньями (П-звеньями). Сравнивающим органом является здесь звено, в котором происходит вычитание входных сигналов:
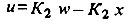
Теперь посмотрим, как будет передаваться сигнал при наличии постоянно-возмущающего воздействия z = z0. Если бы не было регулирования, величина x вместо нулевого приняла бы значение xвозм = Kzz0, где Kz - коэффициент передачи возмущающего воздействия. Чтобы уравновесить это нежелательное воздействие, регулирующее устройство создает (также постоянное) регулирующее воздействие y0. Это вызывает изменение регулируемой величины на
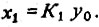
Тогда в статическом состоянии общее значение регулируемой величины будет равно алгебраической сумме этих воздействий:

Но мы хотим, чтобы x0 = w = 0. Добиться этого можно, установив величину регулирующего воздействия
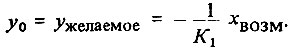
Посмотрим, удастся ли это регулирующему устройству. Чтобы создать воздействие y0, регулирующее устройство должно получить информацию о величине x = x0. Отвечающий за эту информацию измерительный орган в статическом состоянии выдает постоянный сигнал
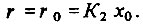
Функция сравнивающего органа состоит в том, что он производит вычитание поступающих в него сигналов и оценивает отклонение регулируемой величины от ее заданного значения. Поскольку, как известно, сравнивать можно только соизмеримые величины, то величина w должна быть приведена к той же размерности, какую имеет величина r . Это делает задающее устройство, преобразующее заданное значение w в K2 w. Выходным сигналом сравнивающего органа является, следовательно, сигнал
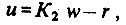
а поскольку w 0, то
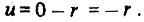
Предположим далее, что усилитель со всеми принадлежностями (исполнительным двигателем и т. д.) также можно представить как пропорциональное звено (в этом случае мы имеем дело с П-регулятором.) В контуре регулирования он создает регулирующее воздействие y = y0:
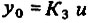
(согласно нашим предпосылкам, оно также является постоянным).
Используя предыдущие расчеты, получаем
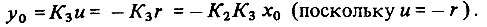
Величина y0 воздействует на объект регулирования, и контур, таким образом, замыкается.
Возникает вопрос, достаточно ли регулирующего воздействия y0 для того, чтобы уравновесить возмущающее воздействие? Если достаточно, то x = x0 = w = 0 и цель регулирования достигнута. Ответить на этот вопрос мы сможем, подставив значение y0 в уравнение (1):
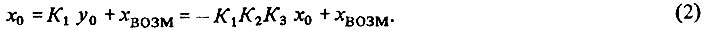
Через обратную связь величина x0 влияет на свое собственное значение. В слагаемом - 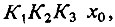 характеризующем обратное воздействие, коэффициент
характеризующем обратное воздействие, коэффициент 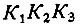 называется усилением контура.
называется усилением контура.
С помощью преобразований получим следующее выражение для x0:
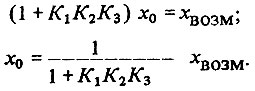
Существенно для нас то, что поскольку 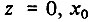 также отличается от нуля и отклоняется от заданного значения
также отличается от нуля и отклоняется от заданного значения 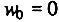 .
.
Задача регулирования: уравнять x и w при наличии помехи z0≠0 - оказывается невыполнимой, по крайней мере, в данном конкретном случае.
Стоит ли тогда вообще применять дорогостоящее регулирование? Стоит, если регулирование может значительно уменьшить отклонение фактического значения от заданного. Для нашего примера это отклонение имеет вид:
без регулирования
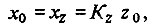
а с регулированием
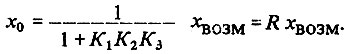
Воздействие регулирования измеряется коэффициентом 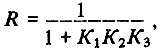 называемым коэффициентом регулирования. Поскольку коэффициенты передачи
называемым коэффициентом регулирования. Поскольку коэффициенты передачи 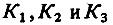 всегда положительны, то и R всегда больше нуля.
всегда положительны, то и R всегда больше нуля.
Регулирование целесообразно, если коэффициенте мал, во всяком случае меньше единицы 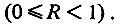
Поясним это на числовом примере. Если, например, мы требуем, чтобы регулирование уменьшило воздействие помехи z0 до 5 % его величины, то
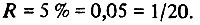
Отсюда можно определить и усиление контура:
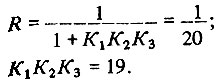
Способен ли контур регулирования на такое усиление, зависит от конкретных условий. К этому вопросу мы еще вернемся.
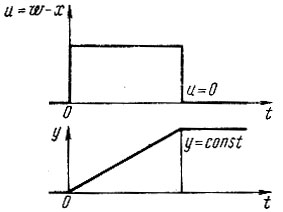
Рис. 46. Переходная функция интегрирующего регулятора (И-регулятора). Регулятор изменяет регулируемое воздействие y до тех пор, пока входной сигнал и не станет равным нулю
Итак, даже в рассмотренном нами простейшем случае техническое регулирование не может выполнить поставленную перед ним задачу или справляется с ней лишь частично. Если бы такую задачу получили мы, люди, то действовали бы совсем по другому: мы пробовали бы различные значения у, пока не добились бы искомого результата: 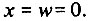 Добившись его, мы зафиксировали бы у на данном уровне. В отличие от П-регулятора, мы не стали бы пытаться заранее определить значение у. Примерно так и работает интегрирующий регулятор (И-регулятор), переходная функция которого изображена на рис. 46.
Добившись его, мы зафиксировали бы у на данном уровне. В отличие от П-регулятора, мы не стали бы пытаться заранее определить значение у. Примерно так и работает интегрирующий регулятор (И-регулятор), переходная функция которого изображена на рис. 46.
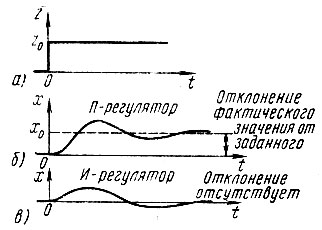
Рис. 47. Характеристика выходного сигнала (регулируемой величины) для П-регулятора и И-регулятора: а - скачкообразно изменяющаяся функция; б - остаточное рассогласование для П-регулятора; в - исчезающее рассогласование для И-регулятора (x0 = 0)
Следовательно, устройство с интегрирующим регулятором может в конечном стационарном состоянии устранить воздействие постоянной помехи z = z0. Этот процесс показан на рис. 47. С переменными помехами эти регуляторы справляются значительно хуже.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'