3. Кибернетика и обучение

3.1. Наша цель - оптимум

Цель наших поступков - не только выполнять стоящие перед нами задачи, но и выполнять их наиболее рациональным, оптимальным способом. Мы продумываем различные варианты, учитывая ограниченность своих сил и скорости реакции, и выбираем тот из них, который с нашей точки зрения является наилучшим. Многие новаторские предложения позволяют выполнять какую-либо работу лучше, чем раньше. Лучше может при этом означать: с меньшими издержками; с меньшими затратами материала или человеческих сил, быстрее и т. д.

Предположим, что нам необходим как можно быстрее, то есть оптимально по времени, привести железнодорожный локомотив в пункт назначения. Решение этой задачи не связано со сложностями, возникающими, например, во время езды на автомобиле по улицам города. Очевидно, что чем больше скорость движения локомотива, тем быстрее он достигнет цели. Однако здесь-то и начинаются проблемы. Скорость движения не может быть сколь угодно большой: она ограничена максимально допустимой скоростью локомотива, а также мощностью, которую он может развивать при разгоне. Выбор оптимального поведения имеет смысл и становится интересной проблемой только, если мы учитываем дополнительные условия (ограничения).

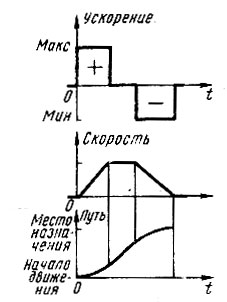
Рис. 65. Оптимальный процесс

На рис. 65 показан график оптимального по времени процесса: нас интересует минимальное время езды t_E = t_{E мин}. Очевидно, необходимо как можно скорее набрать максимально допустимую скорость, поддерживать ее в пути и своевременно со всей силой затормозить, не доезжая места назначения. Если же эти условия не выполняются (например, из-за плохого управления), значит, мы имеем дело с неоптимальным процессом.

Кстати, машинист локомотива обычно не развивает рекордную скорость, а едет со скоростью, обеспечивающей минимальный расход горючего.

Во многих технологических процессах надо прежде всего решить, что именно следует оптимизировать. Например, для контура регулирования можно добиться быстрого затухания колебаний регулируемой величины, но при этом возможно, что амплитуда этих колебаний окажется недопустимо большой. В этом случае процесс оценивается исходя из выбранного показателя качества. Для колебательного процесса, показанного на рис. 66, показателем качества может быть абсолютная площадь под кривой x(t) (сумма отклонений регулируемой величины от ее заданного значения x_B) - так называемая площадь регулирования. Площадь регулирования не может равняться нулю, хотя это, конечно, было бы идеально,- инерционность звеньев контура регулирования обусловлена физическими законами.

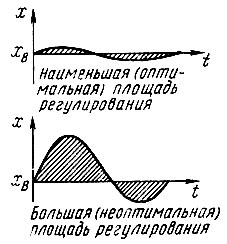
Рис. 66. Площадь регулирования

Разумеется, можно предложить и другой критерий оценки данного контура регулирования. Мы стремились к тому, чтобы регулируемая величина как можно быстрее установилась на постоянном уровне. Но нашей целью может быть и минимальное остаточное отклонение регулируемой величины от заданного значения. В соответствии с другим критерием оценки будет выбран Я другой показатель качества, рассчитываемый на основе наблюдений за сигналами. Показатель качества называется также целевой функцией или функционалом качества. Оптимальное значение показателя качества достигается в ходе настройки регулирующего устройства; правила оптимальной настройки играют большую роль в практике регулирования.

Такого рода показатели качества имеют значение и в повседневной жизни. Например, нам нужно как можно быстрее и дешевле добраться от Карл-Маркс-Штадта до Лейпцига. При этом нам придется иметь дело с двумя различными показателями качества (рис. 67). Разумеется, эти показатели противоречат друг другу, и выбор средства передвижения представляет собой компромисс. Принять решение нам помогут здесь методы многокритериальной оптимизации.

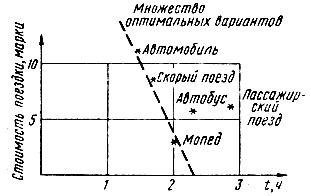
Рис. 67. Выбор средства передвижения представляет собой компромисс между двумя критериями оценки (по времени и по стоимости поездки)

Специалисту-технику также часто приходится принимать подобные решения. При этом он должен выбирать тот или иной критерий оценки. Многокритериальная оптимизация позволяет решать задачу с несколькими критериями качества.

И в повседневной жизни, и в технике мы очень часто встречаем показатели качества, противоречащие друг другу. Например, школьник хочет как можно скорее закончить работу,- учитель же (напротив) требует, чтобы она была сделана как можно лучше. Установление постоянного значения регулируемой величины произойдет быстрее всего, если применять маломощный регулятор (с небольшим коэффициентом передачи K_R), но в этом случае мы получим слишком большое остаточное рассогласование (отклонение от заданного значения). С другой стороны, мы можем добиться минимального остаточного рассогласования, но как показывает опыт, при этом процесс недопустимо затягивается. И здесь на помощь тоже должны прийти методы многокритериальной оптимизации.