Упражнения

1. Покажите, что если C_i = C_i+1 (как определено в теореме 4.3), то C_i = C_i+j для всех j≥0.
2. Покажите, что если C⊆∑^* является максимальным кодом и w∈∑^*, то C^*∩∑^*w∑^*≠∅. (В терминах теории полугрупп это означает, что C^* пересекает все двусторонние идеалы ∑^*.)
3. Покажите, что обращение упр. 2 неверно. (C = {a^2+|w|bw|w∈{a ,b}^*} является префиксным кодом, удовлетворяющим указанному условию, но не максимальным.)
4. Покажите (используя упр. 2), что если C⊆∑^* - конечный максимальный код, то существует слово y∈C^*, такое, что для любого слова x∈∑^* существует слово x'∈∑^* со свойством yxx'∈C^*.
5. Предположим, что C имеет ограниченную задержку слева. Покажите, что существует такое натуральное t, что C^t имеет ограниченную задержку слева, равную двум.
6. Является ли код C = {a, aba baba, bb, bbba} кодом с ограниченной задержкой слева (соответственно справа)? (Заметим, что C является композицией префиксного и суффиксного кодов.)
7. Для заданных m, n≥1 постройте морфизмы g и h, удовлетворяющие условию E(g, h) = {a^mbⁿ}^*. (Ср. с [CuK].)
8. Обозначим через E_k(g, h), k≥0, подмножество множества E(g, h), состоящее из всех таких слов до, что условие (4.19) не выполняется ни для одного префикса x слова до. Покажите, что язык E_k(g, h) регулярен при любых g, h и k. Покажите также, что язык E(g h) регулярен тогда И только тогда, когда E(g, h) = E_k(g, h) для некоторого k. (Заметим также, что E_k (g, h) ⊆E_k+1(g, К) для всех k и что E(g, h) равно объединению множеств Ek(g, h).)
9. Рассмотрим морфизмы
   g, h: {a, b, c, d, e, f}^*→{1, 2, 3, 4, 5}^*,
   заданные таблицей
   
   
   Покажите, что
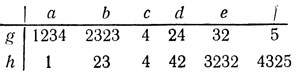   E (g, h) = ({abcb² ... cb²ⁿde²ⁿc ... e²cef|n≥0∪{c})^*
   Выведите отсюда, что множество совпадения префиксного и суффиксного кодов не обязательно регулярно. (В действительности этот конкретный язык E(g, h) даже не является контекстно-свободным.) См. [KaS].
10. Рассмотрим морфизм h, заданный равенствами
    h(a) = de, h(b) = dfe, h(c) = dffe,
    h(d) = a, h(e) = bc, h(f) = ba.
    Докажите, что морфизм h элементарен, в то время как h² упрощаем. Каков наименьший алфавит ∑, для которого вы можете указать два таких элементарных морфизма
    g, h: ∑^*→∑^*.
    что их произведение упрощаемо?
11. Пусть ∑ = {a₁, ..., a_n} и h: ∑^*→∑^*₁ - элементарный морфизм. Покажите, что h имеет задержку, равную
    |h (a₁ ... a_n)| - n + 1,
    как слева, так и справа. Покажите также, что эта оценка, как и оценка p₁ + p₂ - 1, полученная в доказательстве леммы 4.8, является наилучшей возможной в общем случае.
12. Морфизм h: ∑^*→∑^*₁ называется периодическим, если для некоторого слова w h(∑)⊆{w}^*. Покажите, что проблема пустоты E(g, h) разрешима, если хотя бы один из морфизмов g и h является периодическим. (См. [KaS]. Кроме нескольких тривиальных случаев и ситуации, описанной в упр. 13, это единственный известный случай, когда проблема соответствия Поста разрешима.)
13. Исследуйте разрешимость проблемы соответствия Поста в случае, когда алфавиты области определения морфизмов g и h состоят только из двух букв (см. [CuK]). Недавно было показано (см. [EhR5^*]), что проблема соответствия Поста в этом случае разрешима¹. Согласно предыдущему упражнению, этот результат непосредственно вытекал бы из разрешимости проблемы соответствия Поста для элементарных морфизмов, но последний вопрос остается пока открытым. ¹
    Этот результат независимо получил В. А. Павленко (см. [П^*]).- Прим. перев.