5. Разрешимость и неразрешимость

5.1. OL-системы

В этой главе речь идет о вопросах разрешимости. Различие между "разрешимым" и "неразрешимым" иллюстрируется в специфических рамках теории формальных языков: показывается, что некоторая проблема разрешима для некоторого класса языков, но становится неразрешимой, если этот класс несколько расширить.

В нашем изложении "проблемы" состоят из бесконечного числа примеров, и в каждом случае ответом является либо "да", либо "нет". Проблема называется разрешимой, если существует алгоритм, дающий ответ для любого примера (частного случая) проблемы. В противоположной ситуации проблема называется неразрешимой. Как было указано выше, для установления результатов о неразрешимости необходима формализация понятия алгоритма. Мы не даем такой формализации, и наши доказательства неразрешимости состоят в сведении к проблеме соответствия Поста в смысле, указанном в конце гл. 4.

Типичными проблемами разрешимости, которые рассматривает теория формальных языков, являются следующие. Пусть M - некоторый класс устройств для задания языков! (Так, M может состоять, например, из всех грамматик, или всех автоматов некоторого типа, или всех DOL-систем.) Под проблемой языковой эквивалентности для M мы понимаем проблему выяснения для любых двух устройств m₁ и m₂ задают ли они один и тот же язык. Проблема включения для M состоит в том, чтобы для произвольных m₁ и m₂ из M определить, включается ли язык, задаваемый m₁, в язык, задаваемый m₂. Очевидно, что решение проблемы включения дает решение проблемы эквивалентности. Под проблемой пустоты (соответственно конечности) для M мы понимаем проблему определения для произвольного устройства m в M является ли язык, задаваемый m, пустым (соответственно конечным). Проблема принадлежности для M состоит в выяснении для произвольного m из M и произвольного слова до принадлежит ли до языку, задаваемому m.

Так, например, теорема 2.8 дает решение проблемы эквивалентности для конечных автоматов (т. е. в этой теореме M является классом конечных автоматов).

Очевидно, что если некоторая проблема разрешима (соответственно неразрешима) для класса M, то она является таковой же для любого подмножества (надмножества) класса M. Для установления разрешимости (неразрешимости) обычно стараются сделать M как можно большим (соответственно меньшим) с тем, чтобы определить, где именно проходит граница между разрешимостью и неразрешимостью. В дальнейшем мы увидим, что детерминированный и недетерминированный варианты одного и того же класса устройств могут приводить к разрешимой и неразрешимой проблемам языковой эквивалентности соответственно.

Понятия DOL-системы и DOL-языка уже были введены в гл. 1. DOL-системы образуют класс упомянутых выше детерминированных устройств. Теперь мы определим их недетерминированные аналоги, так называемые OL-системы и OL-языки.

Отображение σ алфавита ∑ в множество конечных подмножеств ∑^* называется конечной подстановкой (определенной на ∑). Область определения σ расширяется следующим образом: σ(λ) = {λ}, σ{w₁,w₂) = σ(w₁)σ(w₂) для всех w₁ и w₂ в ∑^*. (Правая часть равенства представляет собой катенацию языков.) Кроме того, для языка L над ∑ положим

В дальнейшем мы будем использовать итерацию конечных подстановок. Таким образом, σⁱ, i≥1, означает i последовательных применений σ. По определению σ⁰(L) = L.

Тройки G = (∑, σ, w), где ∑ - алфавит, σ - определенная на ∑ конечная подстановка, а w - слово над ∑, называются OL-системами. Говорят, что язык

порождается OL-системой G. Языки вида (5.1) называются OL-языками.

Например, OL-системы

порождают соответственно языки

Конечную подстановку в OL-системе можно рассматривать как конечное множество правил подстановки или продукций. Часто выбирают соответствующее обозначение. Так, приведенные выше примеры можно переписать следующим образом:

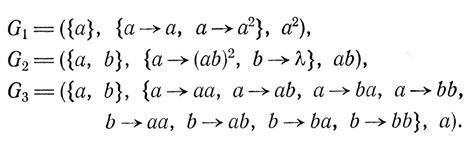
Заметим, что G₂ на самом деле является DOL-системой, поскольку σ₂ можно рассматривать как морфизм. Это всегда имеет место, если для любой буквы а множество σ(a) состоит из одного слова.

Если конечную подстановку σ в OL-системе G рассматривать как конечное множество продукций, то каждое слово x в языке L(G) получается из аксиомы w с помощью вывода

где каждое слово получается из предыдущего заменой каждой буквы в соответствии с некоторой продукцией. В случае DOL-системы этот процесс замены оказывается детерминированным; аксиома однозначно определяет последовательность, если дана длина последовательности. Буква D в названии DOL как раз и означает "детерминированная". DOL- и OL-системы являются частными видами L-систем (обозначение L связано с фамилией Линденмайера, который впервые ввел такие системы в 1968 г. как модели в биологии развивающихся организмов; см. [L]). Существенным свойством L-систем в отличие от систем подстановок или порождающих грамматик, определенных в гл. 2, является параллельность процессов вывода: на каждом шаге процесса заменяется каждая буква. Наконец, буква O в DOL и OL означает, что замещение символов осуществляется контекстно-свободным образом: соседние буквы не влияют на то, чем замещается данная буква. (Первоначально применительно к биологии буква О означала, что связь между отдельными клетками является нульсторонней, т. е. попросту отсутствует.)

Легко проверить, что приведенные выше языки L(G₁) и L(G₃) не являются DOL-языками, т. е. процесс их порождения существенно недетерминирован.

Проблема языковой эквивалентности для DOL-систем (соответственно OL-систем) состоит в определении для любых двух DOL-систем (соответственно OL-систем) G и G', имеет ли место L({G) = L({G'). Последовательность слов S(G), определяемая DOL-системой G, была рассмотрена в гл. 1. Проблема последовательностной эквивалентности для DOL-систем состоит в выяснении для любых двух DOL-систем G и G', имеет ли место S(G) = S(G'). (OL-системы не всегда порождают единственную последовательность слов, и поэтому проблема эквивалентности в указанном выше смысле для OL-систем не определена; см., однако, упр. 13.)

Мы увидим, что проблемы языковой и последовательностной эквивалентности для DOL-систем разрешимы, в то время как проблема языковой эквивалентности для OL-систем неразрешима. Помимо того что эти результаты демонстрируют типичную границу между разрешимостью и неразрешимостью, они очень интересны в историческом плане. Вопрос о разрешимости проблем эквивалентности для DOL-систем довольно долгое время оставался открытым, и его решение вызвало появление новых методов и понятий, таких, как элементарный морфизм и множество совпадения, определенные в предыдущей главе. Исследование проблемы языковой эквивалентности для OL-систем привело к появлению новых идей в теории контекстно-свободных языков.