5.2. Проблемы эквивалентности для DOL-систем

Проблемы языковой и последовательностной эквивалентности для DOL-систем несколько различны, хотя и тесно связаны между собой. Различие состоит в том, что две DOL-системы могут порождать один и тот же язык в разном порядке; типичным примером служат две системы:

Тесная связь этих двух проблем убедительно иллюстрируется тем фактом, что еще за несколько лет до того, как была установлена разрешимость этих проблем, было доказано, что разрешимость одной из них влечет разрешимость другой.

Сначала докажем разрешимость проблемы последовательностной эквивалентности для DOL-систем. Фактически большая часть необходимого для этой цели аппарата содержится в гл. 4. Приведем сначала несколько примеров, выявляющих возникающие здесь трудности.

Рассмотрим две DOL-системы

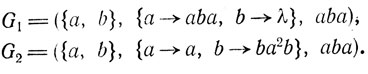
Легко видеть, что

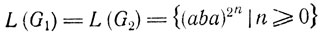
и что S(G₁) = S(G₂) состоит из всех слов в L(G₁) в порядке возрастания длины. Следовательно, G₁ и G₂ языково и последовательностно эквивалентны.

Специфические соображения, подобные проведенным в предыдущем примере рассуждениям, не распространяются на общий случай. Что касается последовательностной эквивалентности, можно по одному порождать слова из двух последовательностей S(G₁) и S(G₂), каждый раз проверяя, совпадают ли i-е слова в двух последовательностях для i = 1, 2, ... . Эта процедура составляет "полуалгоритм" для неэквивалентности: если G₁ и G₂ последовательностно неэквивалентны, то процедура завершается правильным ответом. Но если G₁ и G₂ в действительности последовательностно эквивалентны, то процедура не заканчивается никогда.

Чтобы превратить эту процедуру в алгоритм, надо уметь вычислять число C(G₁, G₂), такое, что если первые C(G₁, G₂) элементов в S(G₁) и S(G₂) совпадают, то S(G₁) = S(G₂). Оказалось, однако, что эта задача очень трудна, хотя, с другой стороны, не исключено, что в качестве C(G₁, G₂) достаточно взять удвоенный объем алфавита G₁ и G₂; во всяком случае, не известен ни один пример, противоречащий этому предположению. Действительно, следующий пример (который можно распространить на большие алфавиты, см. упр. 1) является "худшим" из известных примеров двух DOL-систем G₁ и G₂, таких, что S(G₁)≠S(G₂), но наибольшее (возможное при данном объеме алфавита) число первых слов в этих двух последовательностях совпадает.

Рассмотрим две DOL-системы G₁ и G₂ с аксиомой ab. Продукциями для G₁ (соответственно для G₂) являются

Читатель может проверить, что в последовательностях S(G₁) и S(G₂) первые три слова совпадают, но дальнейшие слова различаются.

После этих примеров перейдем к общему решению проблемы последовательностной эквивалентности для DOL-систем. Будем говорить, что два морфизма g и h (определенные на ∑^*) равны на языке L⊆∑^*, если g(w) = h(w) выполняется для всех w из L. Очевидно, что g и h равны на L тогда и только тогда, когда L⊆E(g, h), где E - множество совпадения, определенное в гл. 4.

Прежде всего докажем две леммы.

Лемма 5.1. Существует алгоритм, позволяющий выяснить, равны ли два морфизма на данном регулярном языке R¹.

¹ (Относительно этой леммы см. замечание переводчика в конце главы.- Прим. ред.)

Доказательство. Пусть A - конечный детерминированный автомат, представляющий R⊆∑^*. Рассмотрим пути в A из начальной вершины в одну из заключительных вершин. Пусть какой-либо из них содержит цикл, т. е. пусть для непустого слова w и некоторых слов w₁ и w₂ все слова w₁wⁿw₂, n≥0, принадлежат R. Тогда мы утверждаем, что либо

либо g и h не равны на R. Действительно, если (5.2) не выполнено, то для достаточно больших n

(

Но поскольку все слова w₁wⁿw₂ принадлежат R, из (5.3) следует, что g и h не равны на R.

Рассмотрим теперь подмножества E_k(g,h) языка E(g,h), определенные в упр. 4.8. Пусть t - число вершин в A, и пусть

где a пробегает ∑. (Здесь рядом с фигурными скобками стоит символ абсолютной величины.) Выберем из множеств E_k(g, h) такое, что k≥^{u(t - 1)}/₂.

Мы можем выяснить, имеет ли место включение

(Указанная возможность следует из того, что оба этих языка регулярны; см. упр. 4.8, а также теоремы 2.7 и 2.8.) Если (5.4) выполняется, то ясно, что g и h равны на R. Обратно, если g и h равны на R, то (5.2) выполняется для всех слов w, таких, что соответствующие им пути из начальной вершины в заключительную содержат петлю. Из этого факта следует, что (5.4) выполняется. В самом деле, мы предположили, что R⊆ E(g, h), и нам известно, что, согласно (5.2), абсолютная величина разности |g(x)| - |h(x)|, где x - префикс некоторого слова из R, не может превышать выбранного нами числа k. Это доказывает правильность (5.4). ▫

Лемма 5.2. Проблема выяснения, содержится ли данный DOL-язык L в данном регулярном языке R, разрешима.

Доказательство. Пусть L = L(G), где G = (∑, h, w) есть DOL-система, и пусть R может быть представлен конечным детерминированным автоматом A. Без потери общности можно предположить, что ∑ является также алфавитом пометок (т. е. входным алфавитом) автомата A.

Построим теперь последовательность автоматов A (h), A(h²), A(h³), ... следующим образом. Для каждого A(hⁱ) множество вершин, начальная и заключительные вершины, а также алфавит пометок совпадают с соответствующими объектами в автомате A. (Из этого факта следует, что все автоматы в нашей последовательности не могут быть различными; в дальнейшем эта информация окажется весьма полезной.) В A (hⁱ) существует помеченная буквой а стрелка из вершины s в вершину s' тогда и только тогда, когда в A существует помеченный словом hⁱ(a) путь из s в s'. Очевидно, что это условие определяет автомат A(hⁱ). Кроме того, R = hⁱ(R_i), где R_i - язык, представляемый автоматом A(hⁱ).

Поскольку не все автоматы в нашей последовательности различны, найдутся такие числа i и j, i<j, что A(hⁱ) = A(h^j). Этот факт влечет равенство

для всех k. Следовательно, каждый автомат из нашей исходной последовательности автоматов является элементом последовательности

(Автоматы из (5.5) не обязательно все различны.)

Пусть теперь R₁ - пересечение языков, представляемых автоматами (5.5) и автоматом A, т. е.

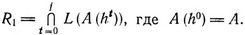
Очевидно, что можно эффективно построить автомат Ль представляющий язык A₁. (Это следует из теоремы 2.7 и того факта, что j можно вычислить эффективно.)

Мы утверждаем, что L⊆R тогда и только тогда, когда w∈L(A₁). (Очевидно, последнее условие разрешимо.) Действительно, L⊆R тогда и только тогда, когда hⁱ(w)∈L(A) для каждого i≥0. Последнее условие выполняется тогда и только тогда, когда для каждого i≥0 имеем w∈L(A(hⁱ)), а это в свою очередь эквивалентно включению w∈L(A₁)).▫

Теперь мы готовы установить первый основной результат, в конечном итоге ведущий к разрешимости проблемы последовательностной эквивалентности для DOL-систем.

Теорема 5.3. Проблема равенства двух данных элементарных морфизмов на данном DOL-языке разрешима.

Доказательство. Чтобы решить вопрос о равенстве двух элементарных морфизмов g₁ и g₂ на языке L(G), где G = (∑, h, w) - некоторая DOL-система, мы поступаем следующим образом. В силу теоремы 4.13 язык E(g\,g2) регулярен. Пусть R₀, R₁, R₂, ... - эффективное перечисление всех регулярных языков над ∑. (Очевидно, такое перечисление возможно. Например, можно рассмотреть сначала конечные детерминированные автоматы с одной вершиной, затем с двумя вершинами и т. д.)

Рассмотрим теперь два полуалгоритма, один для равенства, а другой для неравенства. Последний очевиден: берем последовательность

и проверяем, имеет ли место равенство

g₁(hⁱ(w)) = g₂(hⁱ(w))).

Если морфизмы g₁ и g₂ не равны на L(G), то этот полуалгоритм завершается правильным ответом.

(i + 1)-й шаг полуалгоритма для равенства состоит в проверке с использованием леммы 5.1, равны ли g₁ и g₂ на R_i и в случае положительного ответа в последующей проверке, содержится ли L(G) в R_i. Последнюю проверку можно осуществить с помощью леммы 5.2, и из положительного ответа следует равенство g₁ и g₂ на L(G). (В случае отрицательного ответа на какой-либо из этих вопросов мы переходим к (i+2)-му шагу.) Если морфизмы g₁ и g₂ равны на L(G), то этот полуалгоритм завершается правильным ответом.

Алгоритм для теоремы 5.3 заключается в параллельном применении этих двух полуалгоритмов (т. е. в чередовании их шагов).▫

Вместо абстрактной последовательности R_i, i = 0, 1,2, ..., в предыдущем доказательстве можно рассмотреть конкретную последовательность регулярных языков E_i(g₁, g₂), определенную в упр. 4.8. Тогда (i+1)-й шаг в нашем полном алгоритме состоит в проверке равенства g₁(hⁱ(w)) = g₂(hⁱ(w)) и в случае положительного ответа в проверке включения L(G)⊆E_i(g₁, g₂). Конечно, мы получили бы очень простой алгоритм, основываясь лишь на лемме 5.2, если бы могли эффективно построить регулярный язык E(g₁, g₂). (Напомним, что построение автомата А в доказательстве теоремы 4.9 не было эффективным.)

Проблему последовательностной эквивалентности для DOL-систем можно свести к теореме 5.3. Основная идея этого сведения заключается в декомпозиции морфизма произвольной DOL-системы таким образом, чтобы достаточно было проверить равенство элементарных морфизмов на DOL-языке. В этом плане оказывается полезной следующая лемма.

Лемма 5.4. Пусть h₁ и h₂ - морфизмы из ∑^* в ∑^*. Тогда существуют последовательность i₁, ..., i_m элементов из множества {1,2} и морфизмы f, p₁, p₂, такие, что

причем морфизмы p, элементарны. Кроме того, последовательность i₁, ..., i_m и морфизмы f, p₁, p₂ можно построить эффективно.

Доказательство. Если морфизмы h₁ и h₂ элементарны, то выберем p_j = h_], j = 1, 2. В качестве f возьмем тождественный морфизм, а в качестве последовательности элементов из {1,2} - пустую последовательность.

Предположим теперь, что хотя бы один из морфизмов h₁ и h₂ не элементарен. Рассмотрим составленное из h₁ и h₂ произведение, допускающее максимальное упрощение

Более подробно, мы предполагаем, что (5.7) выполняется для

f: ∑^*→∑₁^* и g: ∑^*₁→∑^*,

где подалфавит ∑₁ имеет меньшую мощность, чем ∑, и если

то мощность алфавита ∑₂ не меньше мощности ∑₁.

Теперь положим p_j = h_jg, j = 1, 2. Тогда (5.7) влечет (5.6). Кроме того, минимальность ∑₁ гарантирует элементарность p₁ и p₂. Действительно, если h_jg допускает упрощение h_jg = g'g", то получаем

где произведение в правой части можно упростить с помощью алфавита меньшей мощности, чем у ∑₁.

Это построение эффективно, потому что при данной произвольной последовательности i₁, ..., i_m можно проверить, выполняется ли (5.6) для некоторого элементарного морфизма p_j. (Вопрос об элементарности данного морфизма легко разрешается, см. упр. 2.) Таким образом, мы просто систематически перебираем все последовательности до тех пор, пока не найдем подходящую. Первая часть доказательства гарантирует, что в конце концов мы получим требуемый результат.

Теперь у нас есть все необходимое для установления основного результата.

Теорема 5.5. Проблема последовательностной эквивалентности для DOL-систем разрешима.

Доказательство. Вез потери общности предположим, что даны две DOL-системы вида

т. е. системы с совпадающими начальными словами и алфавитами. Обозначим слова в последовательностях S(G_i), i = 1, 2, следующим образом:

Пусть теперь i₁, ... , i_m, p₁, p₂, f удовлетворяют лемме 5.4 для h₁ и h₂. Введем обозначения

и рассмотрим DOL-системы

(Заметим, что ∑ может содержать буквы, не входящие фактически в S(G_ij). Однако морфизмы g_i определены на всем ∑.)

Очевидно, если S(G₁) = S(G₂), то для всех j, 0≤j≤m, имеет место

Справедливо также обращение этой импликации, что можно показать при помощи следующего рассуждения от противного. Предположим, что выполняется (5.8), но существует натуральное число n, такое, что w⁽¹⁾_n≠w⁽²⁾_n, и возьмем наименьшее из таких натуральных чисел. Очевидно, что n не может быть меньше m или равно ему, так как в этом случае первые элементы последовательностей S(G_1n) и S(G_2n) были бы различны, что противоречит (5.8). Таким образом, n≥m+1. Выбрав теперь такое натуральное t, что

мы видим, что (t+1)-е слова в последовательностях S(G_1n1) и S(G_2n1) различны, что также является противоречием.

Таким образом, для завершения доказательства нам нужно только установить разрешимость равенств (5.8). С этой целью рассмотрим фиксированное j и положим

Рассмотрим также морфизмы p₁, p₂, f, введенные ранее в этом доказательстве. Можно предположить, что w_f⁽¹⁾ = w_f⁽²⁾ и, следовательно, f (w₁⁽¹⁾) = f(w₁⁽²⁾), поскольку в противном случае S(H₁)≠S(H₂), и вопрос решен.

Рассмотрим теперь DOL-системы

где ∑_i - тот подалфавит алфавита ∑, с помощью которого упрощается морфизм g_i. (В данном случае мы должны взять подалфавит, поскольку морфизм fp_i не обязательно определен на всем ∑.)

По теореме 2.3 можно выяснить, равны ли морфизмы p₁ и p₂ на L(K₁. Но из определений непосредственно следует, что p₁ и p₂ равны на L(K₁) тогда и только тогда, когда S(H₁) = S(H₂).▫

Доказательство разрешимости проблемы языковой эквивалентности для DOL-систем не содержит никаких существенно новых идей в плане теории языков и поэтому опускается. Существенным в этом доказательстве является сопоставление заданной DOL-системе G = (∑, h, w) систем вида

где "период" p достаточно велик, чтобы гарантировать однозначный порядок слов, так что становится применимой теорема 5.5. В процессе работы алгоритм пытается уменьшить период ценой увеличения "первоначального беспорядка" q. Что касается деталей доказательства следующей теоремы, мы отсылаем читателя к упр. 5.

Теорема 5.6. Проблема языковой эквивалентности для DOL-систем разрешима.