5.3. Результаты о неразрешимости

Используем теперь сведение к проблеме соответствия Поста, чтобы доказать, что теорему 5.6 нельзя распространить на OL-системы. В то же время мы докажем неразрешимость проблемы языковой эквивалентности для контекстно-свободных грамматик (см. гл. 2). Оба результата вытекают из приведенной ниже леммы 5.7.

Сентенциальной формой (sentential form) грамматики мы будем называть любое слово α, такое, что S⇒^*α для некоторого начального символа S. Таким образом, сентенциальные формы могут включать как терминалы, так и нетерминалы, в то время как язык L(G), порождаемый грамматикой 6, состоит только из слов в терминальном алфавите.

Лемма 5.7. Проблема, состоящая в выяснении того, порождают ли две данные контекстно-свободные грамматики одно и то же множество сентенциальных форм, неразрешима.

Доказательство. Будем рассуждать от противного, предполагая, что существует алгоритм, выясняющий, совпадают ли множества сентенциальных форм, порождаемые двумя контекстно-свободными грамматиками. Тогда этот алгоритм можно применить следующим образом для решения проблемы соответствия Поста, что и обнаружит ложность сделанного предположения.

Возьмем произвольный пример

проблемы соответствия Поста, где мы положили

Рассмотрим три языка L, L_g и L_h над алфавитом ∑∪∑₁∪{#}. По определению L = ∑^*#∑^*₁. Язык L_g является подмножеством языка L, состоящим из всех слов L, за исключением слов вида

где mi(x) обозначает зеркальный образ (mirror image) слова x, т. е. x, записанное в обратном порядке. (Если x есть λ или состоит только из одной буквы, то mi(x) = x.) Язык L_h определен подобным же образом с заменой в (5.9) морфизма g на h.

Очевидно,

(Напомним, что E(g, h) считается пустым, если состоит лишь из пустого слова.) Опираясь на сделанное нами вначале предположение, построим теперь алгоритм, выясняющий, имеет ли место равенство L = L_g∪L_h. В силу (5.10) этот алгоритм применим также к проблеме соответствия Поста. Определим следующим образом две контекстно-свободные грамматики G₁ и G₂. Единственным начальным символом для обеих грамматик будет S₀, а нетерминальным (терминальным) алфавитом будет

Ниже перечислены продукции грамматики G₁. В этом списке предполагается, что a пробегает ∑, a, b пробегает ₁.

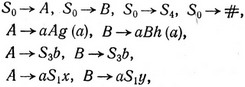
где x (соответственно y) пробегает все слова над ∑₁ имеющих длину меньше |g(a)| (соответственно |h(a)|), включая пустое слово;

где x (соответственно y) пробегает множество всех слов над ∑_i, имеющих длину |g(a)| (соответственно |h(a)|, но отличных от g(a) (соответственно h(a));

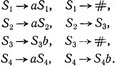
Продукции G₂ получаются из продукций G₁ заменой двух продукций S₁→# и S₃→# на продукцию S₄→#. Этим определение G₁ и G₂ завершается.

Теперь можно непосредственно проверить, что G₁ и G₂ порождают одни и те же сентенциальные формы, за возможным исключением слов, состоящих только из терминальных букв - терминалов. Поэтому, поскольку мы можем решить вопрос о совпадении множеств сентенциальных форм, порождаемых G₁ и G₂, мы можем также решить вопрос, верно ли, что L(G₁) = L(G₂).

Очевидно, что L(G₂) = L. В действительности L выводится по правилам G₂ с использованием только нетерминалов S₀ и S₄. В силу (5.10) и того факта, что мы можем разрешать проблему равенства L(G₁) = L(G₂), для завершения леммы 5.7 достаточно показать, что

Чтобы установить это равенство, покажем, что имеет место включение в обоих направлениях. Пусть слово w принадлежит L(G₁). Надо показать, что w∈L_g∪L_h. Это верно, если w=#. Поэтому предположим, что w≠#. Так как S₄ нельзя устранить, заключаем, что первая продукция, применявшаяся в выводе w, есть S₀→A или S₀→B. В силу симметричности ситуации достаточно рассмотреть первый случай и показать, что w принадлежит L_g. Последовательность различных нетерминалов, появляющихся в выводе w из A, должна быть одной из следующих:

В каждом из этих случаев легко проверить, что w∈L_g. (Часть слова, идущая за центральным маркером #, в первом случае оказывается "слишком длинной", а во втором - "слишком короткой". Третий случай указывает на ошибку в сопоставлении a и g(a).)

Предположим, наоборот, что w∈L_g∪L_h, скажем w∈L_g. Если w∈#∑^*₁, то в грамматике G₁ слово w порождается с помощью продукции

Таким образом, можно предположить, что

Пусть u - наибольшее натуральное число в отрезке 0≤u≤k, такое, что w' = w₁g(a_iu ... a_i1). Предположим сначала, что u = 0, т. е. w' нельзя представить в виде w' = w₁g (a_i1) Если |w'|<|g(a_i1)|, то слово w порождается продукциями.

Если |w'|≥g (a_i1)|, то положим w' = w"x, где |x| = |g(a_i1) и x≠g (a_i1). Слово w может порождаться также продукциями

Теперь предположим, что u = k. В этом случае w' имеет вид

Кроме того, w₁≠λ, так как в противном случае слово w не принадлежало бы языку L_g. Теперь w может порождаться продукциями

Предположим, наконец, что 1≤u<k. Тогда существует такое слово w₁, что

но не существует такого слова w₂, что

Если |w₁|<|g (a_iu+1)|, то w порождается продукциями

В противном случае w₁ можно записать в виде w₁ = w₃x, где |x| = |g(a_iu+1)| и x≠g(a_iu+1). (Напомним, что w' нельзя представить в виде (5.13).) Теперь слово w порождается продукциями

Итак, мы показали, что во всех случаях слово w принадлежит L(G₁).▫

Приведенное доказательство показывает, что в общем случае мы не в состоянии решить проблему равенства множеств сентенциальных форм, порождаемых грамматиками G₁ и G₂ (поскольку не существует соответствующего алгоритма). Грамматики G₁ и G₂ можно преобразовать в OL-системы, добавляя к ним продукции c→c для каждого терминального символа c. Следовательно, проблема языковой эквивалентности для OL-систем неразрешима. (В действительности она остается неразрешимой даже для частного класса OL-систем, а именно для систем, имеющих вид G₁ и G₂. Такие OL-системы, например, не используют λ-продукций.)

Но приведенное выше доказательство показывает также неразрешимость проблемы L(G₁) = L(G₂), когда G₁ и G₂ рассматриваются как контекстно-свободные грамматики. Следовательно, проблема языковой эквивалентности для контекстно-свободных грамматик неразрешима. Из наших рассуждений в действительности следует, что эта проблема остается неразрешимой даже для линейных грамматик, когда ни в одной продукции правая часть не содержит более одного нетерминала.

Таким образом, королларием^* леммы 5.7 является следующий результат.

^* (Под королларием теоремы здесь подразумевается утверждение, вытекающее не только из формулировки этой теоремы, но и из ее доказательства (этим королларий отличается от следствия). - Прим. перев.)

Теорема 5.8. Проблема языковой эквивалентности для OL-систем неразрешима. Проблема языковой эквивалентности для контекстно-свободных грамматик также неразрешима.