Упражнения

1. Докажите, что каждый регулярный язык R можно выразить в виде R = h(L), где L - локальный язык, а морфизм h отображает каждую букву либо в букву, либо в пустое слово. (При этом не делается никаких предположений о принадлежности или непринадлежности пустого слова языку R.)
2. Теоремы 6.7 и 6.8 выявляют порождающую способность инверсных морфизмов. В этом отношении морфизмы значительно слабее: интуитивно ясно, что, когда рассматриваются морфизмы, невозможно никакое "сокрытие". Докажите, что не существует такого языка L₀ типа 0, что каждый язык типа 0 может быть представлен в виде h(L₀). Докажите аналогичное утверждение для контекстно-свободных языков. Эти результаты остаются верными даже в том случае, когда вместо морфизмов берутся конечные подстановки.
3. Порождающая способность морфизмов значительно возрастает, если добавить операцию пересечения с регулярными языками. Теорема 6.10 показывает, что каждый рекурсивно перечислимый язык является морфическим образом пересечения языка перетасовки двойников с регулярным языком. Докажите аналогичный результат для контекстно-свободных языков: каждый контекстно-свободный язык является морфическим образом пересечения языка Дика с регулярным языком. (Этот результат известен как теорема Хомского - Шютценберже.) В этих результатах недостаточно рассматривать какой-либо один язык перетасовки двойников или один язык Дика. Докажите, однако, что для всех контекстно-свободных языков (соответственно языков типа 0) над одним и тем же алфавитом ∑_T достаточно взять один фиксированный язык Дика (соответственно язык перетасовки двойников)^*.
4. Обобщите леммы 6.3 и 6.4 в виде следующей теоремы о "супернормальной форме". Пусть (m, n, p) - произвольная тройка неотрицательных Целых чисел. Тогда каждый контекстно-свободный язык порождается грамматикой, в которой имеются продукции только следующих двух видов: (i) A→w, где w - терминальное слово; (ii) A→w_mBw_nCw_p, где w_m, w_n, w_p суть терминальные слова длиной m, n и p соответственно. (По существу лемма 6.3 дает этот результат для тройки (0, 0, 0), а лемма 6.4 - для тройки (1, 0, 0).) См. [MSW1]. Можно ли усилить условие (i) таким образом, чтобы |w| всегда принадлежало множеству длин рассматриваемого языка? (Множество длин языка состоит из всех длин слов в этом языке.)
5. Проведите доказательство теоремы 6.5 по индукции, выбрав в качестве базиса индукции t = 0. (При этом шаг индукции будет несколько сложнее, чем при базисе t = 1.)
6. Докажите, что язык L₀, определенный перед леммой 6.6, является контекстно-свободным. (Указание. Сначала опишите порождение языка D, как это было сделано выше, но рассматривая терминалы в качестве специальных нетерминалов. Напишите продукции для этих специальных нетерминалов, допуская их преобразование в терминалы либо сразу, либо после передвижения соответствующего слова налево и/или направо.)
7. Рассмотрим контекстно-свободный язык, порождаемый следующей грамматикой G:
   S→a, S→bS, S→cS².
   (Этот язык L известен под названием языка Лукасевича^**.) Дайте представление языка L, соответствующее теоремам 6.5 и 6.7. Исследуйте, в частности, как выводы, соответствующие грамматике G, отражаются в морфизме h (см. [SalS]).
8. Исследуйте связь между числом различных выражений (6.25) для h(w) и "неоднозначностью" слова w в G, т. е. числом различных выводов слова до, соответствующих G.
9. (Для читателя, знакомого с алгеброй.) Рассмотрим отображение Дика ρ. Определим в ∑^* конгруэнтность Ер следующим образом:
   wE_ρw₁ тогда и только тогда, когда ρ (w) = ρ (w₁).
   Получающийся фактормоноид ∑^*\∑_ρ известен под названием инволютивного. Если разрешены двусторонние сокращения, т. е. если выполняются равенства 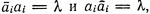то аналогично мы получим свободную группу с множеством образующих ∑₁, равно как и соответствующий язык 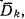состоящий из всех слов, приводимых к λ двусторонними сокращениями. Докажите теоремы о представлении, аналогичные теоремам 6.5 и 6.7, отправляясь от 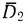вместо D₂. (Эти результаты можно рассматривать как дающие представление языков при помощи свободных групп, а не при помощи инволютивных моноидов.)
10. Не используя тезис Чёрча, докажите, что язык L₀ в доказательстве теоремы 6.8 является языком типа 0. (Построение грамматики типа 0 в явном виде представляет собой весьма трудоемкую задачу. Вместо этого убедитесь в том, что это может быть сделано. Заметьте, в частности, что можно провести выводы между двумя граничными маркерами и посылать "курьеров" от одного маркера к другому. Этим способом можно разбить вывод на шаги таким образом, что новый шаг никогда не начинается до того, как будет выполнено некоторое условие, которое означает окончание предыдущего шага.)
11. Обозначим через e(h₁, h₂) подмножество E(h₁, h₂), состоящее из всех непустых слов до, таких, что никакой собственный префикс слова до (т. е. не равный ни w ни λ) не принадлежит E(h₁, h₂). Докажите, что каждый рекурсивно перечислимый язык над ∑_T можно представить в виде H_∑T(e(h₁, h₂)) (см. [Cu]).
12. Рассмотрите определенные в упр. 4.8 множества E_k(h₁, h₂). Докажите, что язык L регулярен тогда и только тогда, когда существуют такие морфизмы g, h₁, h₂, что L = g(e(h₁, h₂)), и, кроме того,
    e(h₁, h₂)⊆E_k (h₁, h₂) для некоторого k
    (см. [Cu]).
13. Будем говорить, что язык L является языком совпадения, если для некоторых морфизмов h₁ и h₂ он может быть представлен в виде
    L = E(h₁, h₂)
    Покажите, что семейство языков совпадения является наименьшим семейством языков, содержащим L_∑, где ∑ = {a, b}, и замкнутым относительно инверсных морфизмов (см. [EnR]).
14. Усильте теорему 6.10 до следующего утверждения: для каждого рекурсивно перечислимого языка I. над 27 существуют морфизм g и регулярный язык R, такие, что
    L = H_∑T(g^-1(L_{(a, b)})∩R).
15. Докажите теорему 6.11. (Указания. Сначала докажите, что каждый λ-свободный язык типа 0 порождается грамматикой с продукциями видов A→AB, AB→C, A→a. Рассмотрите такую грамматику. Введите для каждого нетерминала A два новых символа y_A и 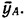Замените каждую продукцию AB→C продукцией A→C_yв. Добавьте все продукции А ~+у~А. Примените теорему 6.7.)

^* (См. замечание переводчика в конце главы.- Прим. ред.)

^** (Если вместо S→a включить несколько продукций S→p₁, ..., S→p_m, заменить b на N, а c на C, то язык L(G) будет состоять из всех пропозициональных формул в бесскобочной (польской) записи сигнатуры (N, C) от переменных p₁, ..., р_m.- Прим. перев.)

Замечание переводчика. Много результатов, относящихся к представлению классов языков с ограниченной сложностью разрешения, содержится в ряде работ (см., например, рефераты в РЖ "Математика", 1983, 2В1037 и 12В1214). В книге [ЯиА*] устанавливаются аналоги теоремы Хомского- Шютценберже (см. упр. 3) для многих классов языков, а именно для полных АСЯ (см. упр. 1 к гл. 7). Новейшие данные приводятся в статье Хиросэ, Окавы и Енеды (Hirose S.. Okawa S., Yoneda M. - Theoret. Comput Sci., 1985, v. 35, p 261-269), где доказывается аналог теоремы Хомского-Шютценберже для рекурсивно перечислимых языков: каждый такой язык является морфическим образом пересечения языка Дика с минимальным линейным языком, т. е. с языком, порождаемым линейной грамматикой с одним нетерминалом. С классами сложности (распознавания) языков читатель может ознакомиться по [СВиА*], [ПМЛ*] и [АУ*].