7. Семейства языков

7.1. Регулярные языки как грамматическое семейство

В предыдущих разделах нам встречались некоторые семейства языков, однако в центре внимания оказывались конкретные семейства, и никакой общей теории семейств языков мы не развивали. Такая теория может основываться на свойствах замкнутости: в ней исследуются семейства языков, замкнутые относительно нескольких заданных операций. Ряд дополнительных фактов и касающиеся этого подхода ссылки даны в упр. 1 и 2. Следуя основной идее настоящей книги, мы рассмотрим теперь теорию семейств языков, основанную на морфизмах. Этот подход означает приблизительно следующее.

Исходя из фиксированной грамматики G, так сказать "главной грамматики", мы рассматриваем инверсные морфические образы G (в уточняемом ниже смысле). Их можно рассматривать как грамматики, "подобные" G. Каждый инверсный морфический образ G порождает некоторый язык. Теперь с произвольной главной грамматикой G можно связывать некоторое семейство языков, а именно языков, порожденных инверсными морфическими образами G. В этой главе мы займемся такими семействами языков, известными под названием грамматических семейств. Мы ограничимся рассмотрением контекстно-свободных главных грамматик.

Среди определенных таким образом грамматических семейств мы встретим наших старых знакомых, например семейства регулярных и контекстно-свободных языков. Поскольку параллельные подстановки носят существенно иной характер, мы не найдем среди них ни DOL-, ни OL-языков. Можно построить аналогичный механизм для задания L-семейств (см. [RS] или [W]).

Давая естественную модель подобия грамматик, теория главных грамматик и грамматических семейств является также естественным способом изучения всех возможных нормальных форм грамматик, порождающих конкретные семейства языков. Ниже будут приведены примеры этого процесса. Мы укажем также способ построения "многих" грамматических семейств, фактически даже плотных иерархий таких семейств. Наконец, мы покажем, каким образом один частный случай этой теории связан с задачей о раскраске графа.

Начнем с некоторых формальных деталей.

Рассмотрим грамматику G с множеством продукций P, нетерминальным и терминальным алфавитами ∑_N и ∑_T и множеством начальных символов ∑_S⊆∑_N. Пусть

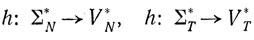
есть побуквенный морфизм, и пусть каждая буква из V_N∪V_T является некоторым h-образом. Таким образом, мощность V_N (соответственно V_T) не превосходит мощности ∑_N (соответственно ∑_T) и можно записать

Множество h(P) естественным образом определяется как

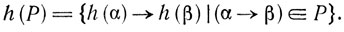
Теперь заметим, что G₁ = (V_N, V_T, h(P), h(∑_S)) также является грамматикой. Назовем G₁морфическим образом G и обозначим

Требование, чтобы h был побуквенным морфизмом, существенно, потому что в противном случае мы не могли бы получить собственные алфавиты для новой грамматики G₁.

Грамматика G = (∑_N, ∑_T, P, ∑_S) является подграмматикой грамматики G' = (∑'_N, ∑'_T, P', ∑'_S), если ∑_N⊆∑_N', ∑_S⊆∑_S', ∑_T⊆∑_T' и P⊆P'.

Грамматика G называется инверсным морфическим образом грамматики G'₁, если (7.1) выполняется для некоторого побуквенного морфизма h и подграмматики G₁ грамматики G₁'. Тот факт, что G является инверсным морфическим образом G₁' при (побуквенном) морфизме h, записывается так:

Читатель может удивиться, почему соотношения (7.1) и (7.2) не симметричны. "Суперграмматика" G'₁ грамматики G₁ введена в (7.2) для того, чтобы обеспечить большую свободу выбора: одна грамматика является инверсным морфическим образом другой грамматики, если первую можно морфически отобразить на подграмматику второй. Это весьма существенно: мы хотим, чтобы можно было использовать только подмножество множества всех продукций. Дальнейшая информация содержится в упр. 3.

Семейство языков, порожденное грамматикой G, определяется следующим образом:

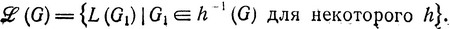
Семейство языков называется грамматическим, если = 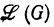для некоторой G. Если к тому же G - контекстно-свободная грамматика, то 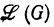называется контекстно-свободным грамматическим семейством. Все грамматические семейства и грамматики, обсуждаемые в этой главе, являются контекстно-свободными, даже если это не указывается в явном виде.

Во избежание ненужных частных случаев в этой главе мы рассмотрим только λ-свободные языки. Говоря об отдельных семействах языков, таких, как семейства регулярных или контекстно-свободных языков, мы будем подразумевать совокупности λ-свободных языков в этих семействах.

В качестве примера рассмотрим грамматику, заданную продукциями

Из леммы 6.3 непосредственно следует, что грамматическое семейство, порожденное этой грамматикой, представляет собой семейство всех контекстно-свободных языков. Аналогично из леммы 2.2 следует, что грамматика

порождает семейство всех регулярных языков.

Две грамматики G₁ и G₂ называются эквивалентными по семействам, если (G₁) = (G²)^*. (Напомним, что G₁ и G₂ называются эквивалентными, если L(G₁) = L(G₂).) Очевидно, что две грамматики могут быть эквивалентными по семействам, не будучи эквивалентными, и обратно. Например, грамматики (7.3) и (7.4) эквивалентны (обе порождают язык a⁺), но не эквивалентны по семействам. С другой стороны, переименование терминального алфавита грамматики G (например, приписывание штрихов всем терминалам) оставляет семейство 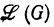без изменений и в то же время изменяет язык L(G) (за исключением тривиального случая, когда L(G) не содержит непустых слов).

^* (Таким образом, проблема эквивалентности грамматик G₁ и G₂ по семействам является проблемой равенства грамматических семейств.- Прим. перев.)

Грамматика называется регулярно-полной (соответственно регулярно-достаточной), если порождаемое ею семейство равно семейству регулярных языков (соответственно содержит это семейство). Так, обе грамматики (7.3) и (7.4) являются регулярно-достаточными, а (7.4), кроме того, является регулярно-полной. Грамматика называется контекстно-свободно-полной или, короче, полной, если порождаемое ей семейство равно семейству контекстно-свободных языков. (Напомним, что мы рассматриваем только контекстно-свободные грамматики. Так как морфизмы и инверсные морфизмы сохраняют свойство бесконтекстности, то наибольшим семейством, порождаемым некоторой грамматикой, является семейство контекстно-свободных языков. Таким образом, нет смысла говорить о контекстно-свободной достаточности!) Грамматика (7.3) является полной.

Понятия полноты и достаточности можно определить и для других семейств языков. Заметим, что каждая полная грамматика дает некоторую "нормальную форму" для контекстно-свободных грамматик. Так, (7.3) дает нормальную форму Хомского из леммы 6.3. Следовательно, характеризация полноты одновременно является характеризацией всех возможных нормальных форм для контекстно-свободных грамматик. То же самое в равной степени справедливо для других семейств: характеризация регулярной полноты одновременно является характеризацией всех возможных нормальных форм грамматик для регулярных языков. Такая характеризация приводится ниже.

В литературе инверсные морфические образы грамматик часто называют интерпретациями. Кроме того, если рассматриваются семейства языков, а не сами языки, то грамматики часто называют схемами грамматик (реже грамматическими формами, grammar forms). Инверсный морфизм можно заменить прямой операцией конечной подстановки; это делается следующим образом. Рассмотрим грамматику G = (∑_N, ∑_T, P, ∑_S) и конечную подстановку σ, определенную на алфавите ∑_N∪∑_T и такую, что σ(a) является конечным (возможно, пустым) множеством букв для каждой буквы a и a≠b всегда влечет σ(a)∩σ(b) = ∅. Положим

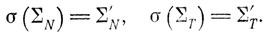
Пусть ∑'_S - подмножество из σ(∑_S), a P' - подмножество из σ(P) (где последнее определяется естественным образом). Тогда грамматика

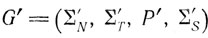
называется интерпретацией грамматики G. Очевидно, что данное понятие интерпретации совпадает с приведенным выше, т. е. с понятием инверсного морфического образа. Множество всех интерпретаций G обозначим через M(G).

Следующие три леммы непосредственно вытекают из определений, и поэтому мы опускаем их доказательства.

Лемма 7.1. Существует алгоритм, выясняющий для двух данных грамматик G и G₁, будет ли G₁ интерпретацией грамматики G. Если G₁ - интерпретация G, а G₂ - интерпретация G₁, то грамматика G₂ также является интерпретацией G. Следовательно, если G₁ - интерпретация G, то семейство языков, порождаемое грамматикой G₁, содержится в семействе, порождаемом грамматикой G.

Лемма 7.2. Для каждого языка L из 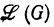существует такой побуквенный морфизм h, что h(L)⊆L(G). Следовательно, множество длин каждого языка из 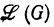содержится в множестве длин языка L(G).

Лемма 7.3. Язык L(G) конечен тогда и только тогда, когда конечен каждый язык в 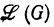. Если

конечен, то грамматика G эквивалентна по семействам грамматике, задаваемой продукциями

Выведем теперь характеризации регулярной полноты и регулярной достаточности. Прежде всего нам потребуются два определения.

Пусть a - буква в терминальном алфавите грамматики G (контекстно-свободной, как было оговорено выше). a-ограничение G_a грамматики G получается из G удалением всех терминалов, не равных а, и всех продукций, содержащих какие-либо из них.

Грамматика G называется грамматикой с самовставлением, если в ней имеется вывод

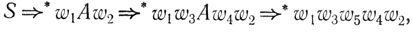
где S∈∑_S, w_i суть терминальные слова и w₃≠λ, w₄≠λ.

Лемма 7.4. Семейство языков грамматики G содержит нерегулярный язык тогда и только тогда, когда G является грамматикой с самовставлением.

Доказательство. Предположим, что G является грамматикой с самовставлением, и рассмотрим вывод (7.5). Отобрав входящие в этот вывод продукции и взяв "штрихованные" двойники букв, представленных в w₄, мы получим интерпретацию G₁ грамматики G, такую, что

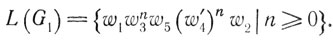
Очевидно, язык L(G₁) нерегулярен, и, следовательно, семейство 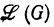содержит нерегулярный язык.

Наоборот, пусть G не является грамматикой с самовставлением. Если в некоторой интерпретации G₁ грамматики G имеется вывод (7.5), то рассмотрим побуквенный морфизм, фигурирующий в определении G₁, и таким образом получим вывод вида (7.5), также соответствующий G. Поскольку это невозможно, мы заключаем, что ни одна интерпретация и не является грамматикой с самовставлением. Так как каждая грамматика без самовставления порождает регулярный язык (это легко проверить), то 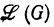состоит только из регулярных языков.▫

Лемма 7.5. Грамматика G регулярно-достаточна тогда и только тогда, когда для некоторой терминальной буквы a язык a⁺ содержится в L(G). Последнее условие выполняется тогда и только тогда, когда существует такое ограничение G_a грамматики G, что имеет место L(G_a) = a⁺.

Доказательство. Второе утверждение очевидно. Из леммы 7.2 непосредственно следует также, что если в G нет такого терминального символа a, то в семействе 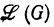нет языков вида b⁺, где b - буква, и, следовательно, G не является регулярно-достаточной.

Пусть у G есть такое a-ограничение G_a, что L(G_a) = a⁺. Рассмотрим произвольный регулярный язык R⊆∑⁺ и докажем, что R принадлежит (G_a). Следовательно, R принадлежит также 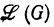, откуда вытекает регулярная достаточность грамматики G.

Для построения интерпретации G₁ грамматики G_a, порождающей данный язык R, мы применим стандартную конструкцию с тройками (см. упр. 2.11). Нетерминалами G₁ будут тройки (q, A, q'), где A - нетерминал из G_a, а g и q' - вершины конечного детерминированного автомата, представляющего R. Такая тройка представляет собой интерпретацию A, т. е. принадлежит множеству σ(A). Начальными символами G₁ являются тройки (q₀, S, q_F), где q₀ (соответственно q_F) - начальная (соответственно заключительная) вершина автомата, а S - начальный символ G_a. Множество терминалов G₁ равно ∑, т. е. каждая буква из ∑ принадлежит σ(a).

Пусть P_a - множество продукций грамматики G_a. Множество продукций G₁ является подмножеством σ(P_a), которое сохраняет как выводы грамматики G_a, так и переходы автомата. Например, если A→BaCC является продукцией G_a, то множество продукций грамматики G₁ содержит все продукции

где q_i - вершины автомата, а b - буква из ∑, вызывающая переход из q₃ в q₄. Если A→ab является продукцией грамматики G_a, то множество продукций G₁ содержит все продукции

где q_i - такие вершины автомата, что слово ab вызывает переход из q₁ в q₂.

Теперь читатель без труда сможет формально определить множество продукций грамматики G₁ и показать, что L(G₁) = R. ▫

Следующая теорема является непосредственным следствием лемм 7.4 и 7.5. Единственный необходимый дополнительный факт - разрешимость свойства грамматики быть грамматикой с самовставлением - устанавливается достаточно просто; детали оставляются читателю.

Теорема 7.6. Грамматика G является регулярно-полной тогда и только тогда, когда она не является грамматикой с самовставлением и имеет a-ограничение G_a, такое, что L(G_a) = a⁺. Свойство регулярной полноты грамматики G разрешимо.

Теорема 7.6 показывает также, что семейство регулярных языков обладает следующим свойством. Если грамматика G порождает семейство , то некоторое ее a-ограничение G_a также порождает . Таким образом, в грамматике G "существенной" является только одна терминальная буква; см. также упр. 7.