7.2. Плотная иерархия грамматических семейств
Среди грамматических семейств представляют значительный интерес лишь некоторые широко исследуемые семейства., такие, как семейства регулярных, линейных и контекстно-свободных языков. Однако в целом существует "очень много" грамматических семейств в силу замечательной порождающей способности морфизмов. Чтобы формально доказать это утверждение, начнем с некоторых определений.
Пусть  и
и  ' - такие грамматические семейства, что
' - такие грамматические семейства, что  ⊆
⊆ '. Пара (
'. Пара ( ,
,  ') называется плотной, если для любых грамматических семейств
') называется плотной, если для любых грамматических семейств  1 и
1 и  2, таких, что
2, таких, что
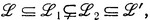
существует такое грамматическое семейство  3, что
3, что  1
1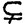
 3
3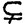
 2. (Было бы ошибкой считать семейства между
2. (Было бы ошибкой считать семейства между  и
и  ' линейно-упорядоченными; в общем случае среди них будет много несравнимых семейств.)
' линейно-упорядоченными; в общем случае среди них будет много несравнимых семейств.)
Грамматическое семейство  2 называется последователем грамматического семейства
2 называется последователем грамматического семейства  1 (а
1 (а  1 называется предшественником
1 называется предшественником 2), если
2), если  1
1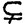
 2 и не существует грамматического семейства
2 и не существует грамматического семейства  3 со свойством
3 со свойством  1
1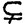
 3
3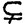
 2.
2.
Рассмотрим в качестве примера грамматику G и натуральное число k≥1, не принадлежащее множеству длин языка L(G), (Определение множества длин дано в упр. 6.4.)
Пусть b1, ..., bk - новые различные терминальные символы, а G1 - грамматика, получающаяся из G добавлением продукции
S→b1 ... bk.
(Как обычно, S обозначает начальный символ.) Тогда легко проверить, что  (G1) является последователем 3'{G). Самое существенное здесь то, что все символы b различны и отличаются от терминальных символов грамматики G. Предполагается также, что символ S не входит в правые части продукций.
(G1) является последователем 3'{G). Самое существенное здесь то, что все символы b различны и отличаются от терминальных символов грамматики G. Предполагается также, что символ S не входит в правые части продукций.
Например, если G определяется продукциями
S→A, A→a2, A→a2,
то, повторяя указанное выше построение, мы получим бесконечную последовательность грамматических семейств, в которой каждое семейство, начиная со второго, является последователем предыдущего семейства (в смысле данного выше определения), а первым является  (G).
(G).
Следовательно, если множество длин языка L(G') содержит в собственном смысле множество длин языка L(G), то пара ( (G),
(G), (G')) не может быть плотной. С другой стороны, известно много плотных пар семейств, для которых множества длин, соответствующих порождающим их грамматикам, совпадают. Мы хотим показать, что семейства регулярных и контекстно-свободных языков образуют плотную пару.
(G')) не может быть плотной. С другой стороны, известно много плотных пар семейств, для которых множества длин, соответствующих порождающим их грамматикам, совпадают. Мы хотим показать, что семейства регулярных и контекстно-свободных языков образуют плотную пару.
В доказательстве теоремы важную роль играет приведенная ниже лемма. Прежде чем мы ее сформулируем, введем еще одно вспомогательное понятие. Язык L называется когерентным, если его нельзя представить в виде L = L1∪L2, где L1 и L2 - языки над непересекающимися алфавитами и как L1, так и L2 содержит хотя бы одно непустое слово. Таким образом, язык {ab, bc, dc) когерентен, тогда как язык {a, bc} не когерентен.
Лемма 7.7. Пусть  1 и
1 и  2 - такие грамматические семейства, что
2 - такие грамматические семейства, что  1
1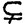
 2 и, кроме того, существует бесконечный когерентный язык L, принадлежащий
2 и, кроме того, существует бесконечный когерентный язык L, принадлежащий  2\
2\ 1. Тогда существует грамматическое семейство
1. Тогда существует грамматическое семейство  3, такое, что
3, такое, что
 1
1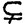
 3
3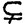
 2(7.6)
2(7.6)
Доказательство. Обозначим через Li (i = 1, 2, ...) подмножество языка L, состоящее из всех слов длины ≠i. Мы хотим показать, что для некоторого pLp∉ 1 и Lp≠L.
1 и Lp≠L.
Поскольку язык L бесконечен, Li≠L для бесконечного множества значений i. Предположим, что все такие Li принадлежат семейству  1 и что грамматика G1 порождает семейство
1 и что грамматика G1 порождает семейство  1, а Hi является порождающей язык Li интерпретацией грамматики G1. Для каждого i существует побуквенный морфизм hi, отображающий Hi на подграмматику G1. Так как терминальный алфавит каждой грамматики Hi содержится в алфавите языка L, то существуют два различных числа i и j, таких, что ограничения hi и hj на терминалы идентичны. (Это, очевидно, вытекает из того, что для любых алфавитов ∑ и Δ существует лишь конечное число побуквенных морфизмов h: ∑*→Δ*.)
1, а Hi является порождающей язык Li интерпретацией грамматики G1. Для каждого i существует побуквенный морфизм hi, отображающий Hi на подграмматику G1. Так как терминальный алфавит каждой грамматики Hi содержится в алфавите языка L, то существуют два различных числа i и j, таких, что ограничения hi и hj на терминалы идентичны. (Это, очевидно, вытекает из того, что для любых алфавитов ∑ и Δ существует лишь конечное число побуквенных морфизмов h: ∑*→Δ*.)
Рассмотрим теперь языки Li и Lj. Без потери общности можно предположить, что нетерминальные алфавиты грамматик Hi и Hj не пересекаются. Естественным образом определив объединение морфизмов и объединение грамматик, мы видим, что объединение h морфизмов hi и hj удовлетворяет соотношению
Hi∪Hj∈h-1(G1).
(Для этого заключения необходимо, чтобы hi и hj отображали терминалы одинаковым образом.) Но это означает, что язык Li∪Lj = L принадлежит  1, а это противоречит нашей гипотезе.
1, а это противоречит нашей гипотезе.
Следовательно, существует число p, такое, что Lp∉ 1 и Lp≠L. Очевидно, что любое переименование нетерминальных и терминальных символов грамматики оставляет неизменным порождаемое ею семейство. В дальнейшем будем считать, что G1 и Hp (грамматика для Lp) не содержат общих букв (в случае необходимости мы переименуем алфавиты грамматики G1).
1 и Lp≠L. Очевидно, что любое переименование нетерминальных и терминальных символов грамматики оставляет неизменным порождаемое ею семейство. В дальнейшем будем считать, что G1 и Hp (грамматика для Lp) не содержат общих букв (в случае необходимости мы переименуем алфавиты грамматики G1).
Рассмотрим объединение G3 грамматик G1 и Hp (таким образом, каждый элемент в G3 является объединением соответствующих элементов в G1 и Hp) и положим  3 =
3 =  (G3). Мы утверждаем, что выполняется (7.6).
(G3). Мы утверждаем, что выполняется (7.6).
По определению G3 семейство  3 содержит
3 содержит  1. Это включение является собственным, поскольку Lp≠
1. Это включение является собственным, поскольку Lp≠ 1, но, очевидно, Lp∈
1, но, очевидно, Lp∈ 3.
3.
Так как L∈ 2, то и Lp∈
2, то и Lp∈ 2 (Это утверждение следует из результата, приведенного в упр. 6, но его можно проверить и непосредственно, модифицируя порождающую L грамматику таким образом, что все слова длины ≤p получаются непосредственно из начального символа; см. также второе утверждение леммы 7.3.) Следовательно, можно предположить, что Hp является интерпретацией грамматики G2, порождающей семейство
2 (Это утверждение следует из результата, приведенного в упр. 6, но его можно проверить и непосредственно, модифицируя порождающую L грамматику таким образом, что все слова длины ≤p получаются непосредственно из начального символа; см. также второе утверждение леммы 7.3.) Следовательно, можно предположить, что Hp является интерпретацией грамматики G2, порождающей семейство  2. Согласно последнему утверждению леммы 7.1, семейство
2. Согласно последнему утверждению леммы 7.1, семейство  (Hp) является частью
(Hp) является частью  2.
2.
Заметим теперь, что каждый язык из  3 имеет вид K1∪K2, где K1∈
3 имеет вид K1∪K2, где K1∈ 1, K2∈
1, K2∈ (Hp) и, кроме того, алфавиты языков K1 и K2 не пересекаются. Из того что оба семейства
(Hp) и, кроме того, алфавиты языков K1 и K2 не пересекаются. Из того что оба семейства  (Hp) и
(Hp) и  1 содержатся в
1 содержатся в  2, следует, что и
2, следует, что и  3 содержится в
3 содержится в  2. (Здесь непересечение алфавитов является весьма существенным; в противном случае сделанное заключение не обязательно справедливо.)
2. (Здесь непересечение алфавитов является весьма существенным; в противном случае сделанное заключение не обязательно справедливо.)
Теперь используем тот факт, что язык L когерентен. Из него следует, что язык L, принадлежащий  3, должен содержаться в одной из частей
3, должен содержаться в одной из частей  3, т. е. либо в
3, т. е. либо в  1, либо в
1, либо в  (Hp). Первый вариант исключается по предположению, а второй в силу того (см. лемму 7.2), что ни один язык в
(Hp). Первый вариант исключается по предположению, а второй в силу того (см. лемму 7.2), что ни один язык в  (Hp) не содержит слов длины p. Так как Lp≠L, то язык L содержит хотя бы одно слово длины p.
(Hp) не содержит слов длины p. Так как Lp≠L, то язык L содержит хотя бы одно слово длины p.
Следовательно, язык L принадлежит разности  2\
2\ 3, что завершает проверку (7.6).▫
3, что завершает проверку (7.6).▫
Теорема 7.8. Грамматические семейства регулярных и контекстно-свободных языков образуют плотную пару.
Доказательство. Рассмотрим два произвольных грамматических семейства  1 и
1 и  2,
2,  1
1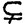
 2 лежащие между семействами регулярных и контекстно-свободных языков. Стало быть, в разности
2 лежащие между семействами регулярных и контекстно-свободных языков. Стало быть, в разности  2\
2\ 1 содержится некоторый язык L. Так как
1 содержится некоторый язык L. Так как  1 содержит все регулярные, а значит, и все конечные языки, то язык L бесконечен. Чтобы стало возможным применение леммы 7.7, надо еще показать, что язык L когерентен. Конечно, это не обязательно имеет место для произвольного языка L из разности
1 содержит все регулярные, а значит, и все конечные языки, то язык L бесконечен. Чтобы стало возможным применение леммы 7.7, надо еще показать, что язык L когерентен. Конечно, это не обязательно имеет место для произвольного языка L из разности  2\
2\ 1. Однако мы покажем, что каждый L содержит бесконечное когерентное подмножество U, принадлежащее разности
1. Однако мы покажем, что каждый L содержит бесконечное когерентное подмножество U, принадлежащее разности  2\
2\ 1.
1.
Итак, пусть язык L не когерентен: L = L1∪L2, где L1 и L2 - языки над непересекающимися алфавитами (и каждый из языков L1 и L2 содержит хотя бы одно непустое слово). Оба языка L1 и L2 принадлежат  2, потому что L лежит в
2, потому что L лежит в  2. (Это опять-таки следует либо из упр. 6, либо доказывается непосредственно, исходя из грамматики для L.) Если оба языка L1 и L2 принадлежат
2. (Это опять-таки следует либо из упр. 6, либо доказывается непосредственно, исходя из грамматики для L.) Если оба языка L1 и L2 принадлежат  1, то язык L также должен принадлежать
1, то язык L также должен принадлежать  1, а это невозможно. Значит, один из языков, скажем L1, не принадлежит
1, а это невозможно. Значит, один из языков, скажем L1, не принадлежит  1. Из этого следует бесконечность L1 (так как
1. Из этого следует бесконечность L1 (так как  1 содержит все конечные языки).
1 содержит все конечные языки).
Таким образом, мы нашли бесконечный язык L1, принадлежащий разности  2\
2\ 1. Кроме того, язык L\ оказывается над меньшим алфавитом, чем L. Если язык L1 не когерентен, то повторяется та же процедура. После конечного числа шагов мы найдем бесконечный когерентный язык L', принадлежащий разности
1. Кроме того, язык L\ оказывается над меньшим алфавитом, чем L. Если язык L1 не когерентен, то повторяется та же процедура. После конечного числа шагов мы найдем бесконечный когерентный язык L', принадлежащий разности  2\
2\ 1. Далее применяется лемма 7.7.▫
1. Далее применяется лемма 7.7.▫
Эффективность проведенного построения обсуждается в упр. 8.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'