3.1. Состояния

Рассмотрим некоторый организм, взаимодействующий со средой. Поведение среды оказывает определенные влияния на организм - мы будем говорить об этих влияниях как о входах организма; в то же время некоторые аспекты деятельности организма - мы будем называть их выходами - оказывают влияние на поведение среды (рис. 32). Строя наши обобщающие теории, мы обязаны постоянно подчеркивать (хотя в приводимых моделях этот факт может быть недостаточно акцентирован), что мы имеем дело не с какими-то изолированными пассивными организмами, подвергаемыми воздействиям откуда-то извне, но с организмами, находящимися в постоянной взаимосвязи со средой. Выходы организма можно рассматривать как входы среды и наоборот.

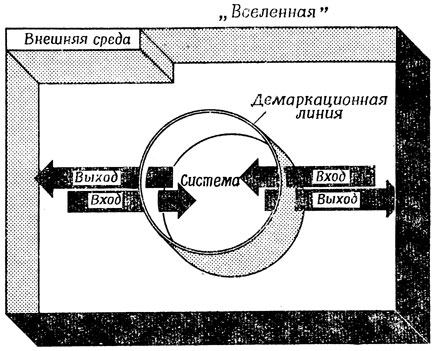
Рис. 32. Здесь показано, как любой 'мир' можно разбить на две части: на 'систему', которая является основным объектом исследования, и 'внешнюю среду', содержащую все те аспекты остальной части мира, которые оказывают влияние на поведение системы

В теории систем входами и выходами считается лишь небольшая доля взаимодействий рассматриваемой системы с остальной Вселенной, т. е. только те взаимодействия, которые, по предположению ученого, играют важную роль в определении наблюдаемого поведения системы. Если взять, например, автомат по продаже конфет, то его входными воздействиями разумно считать лишь акт "опустили деньги в щель и потянули за рычаг", не рассматривая при этом ни напряжения, необходимого для питания электрического механизма автомата, ни те проклятия и удары, которыми мы осыпаем его в случае сбоя. Аналогичным образом среди его выходов мы не станем упоминать возможный удар током, но выдаст ли он конфету или конфету и сдачу - это нам важно.

По существу число переменных, которое можно включать в анализ систем, ничем не ограничено - искусство хорошего теоретического анализа в том и состоит, чтобы отобрать из всей массы имеющихся взаимодействий действительно содержательные. Теория человеческого познания могла бы, конечно, принимать в расчет даже силу ветра или температуру в левой подмышке, однако нет никаких оснований рассчитывать на то, что включение в анализ подобных эксцентричных переменных приведет к лучшим результатам. Правильно выбранные переменные - решающий момент в любом теоретическом построении.

Независимо от того, насколько удачен наш выбор входов и выходов, мы не можем тем не менее надеяться, что они позволят нам полностью описать поведение системы. Нельзя предугадать ответ человека, если неизвестны сведения, которыми он располагает по данному вопросу; точно так же, не зная заложенную в ЭВМ программу, мы не сможем сказать, что она сделает с введенными в нее данными (см. разд. 3.2). Короче говоря, нельзя надеяться до конца понять процессы мышления, если следовать тем психологам, которые считают, что любой организм пассивно реагирует на последовательность стимулов и что им можно управлять с помощью определенной программы подкреплений. Чтобы достигнуть успеха, необходимо иметь также описание внутреннего состояния системы, которое определяет, какие именно из имеющихся в данный момент стимулов будет использовать организм, принимая решение о своих текущих действиях и изменении своего внутреннего состояния. Точно так же теории, обобщающие описанные здесь концепции, должны учитывать аналогичные моменты для внешней среды.

Чтобы сформулировать роль, которую играет внутреннее состояние, разберем более подробно работу торгового автомата (рис. 33). Когда мы опускаем в щель достаточное количество денег и тянем за рычаг под картинкой, изображающей нужный нам предмет, мы рассчитываем на однозначную реакцию автомата: он должен выдать нам соответствующий предмет и правильную сдачу. На самом деле автомат выдает нам самый нижний предмет из стопки над рычагом. Но это произойдет лишь в том случае, если в автомате имеется достаточное количество понадобившегося нам товара, а для того чтобы автомат правильно сдал нам сдачу, в нем должен быть запас соответствующих монет. Таким образом, выход автомата не всегда зависит только от поступившего стимула. В начале дня, когда весь товар только что уложен и есть любая сдача, автомат некоторое время действует по нормальной схеме "стимул - реакция", но в какой-то момент запас конфет или мелких монет иссякает, и такое описание работы автомата становится ошибочным. Чтобы описать реакцию автомата на входное воздействие, нам необходимо знать, что лежит внизу каждой стопки и какая мелочь имеется в бункере. Однако для того, чтобы описать поведение машины на протяжении более длительных промежутков времени, этого недостаточно, ибо, извлекая один предмет, мы создаем новую ситуацию, в которой следующий выход машины определяется тем предметом, который лежал над купленным нами. Таким образом, этот крайне простой пример показывает, что полное описание внутреннего состояния системы должно содержать полный упорядоченный перечень предметов в каждой стопке и полное перечисление всей мелочи на сдачу.

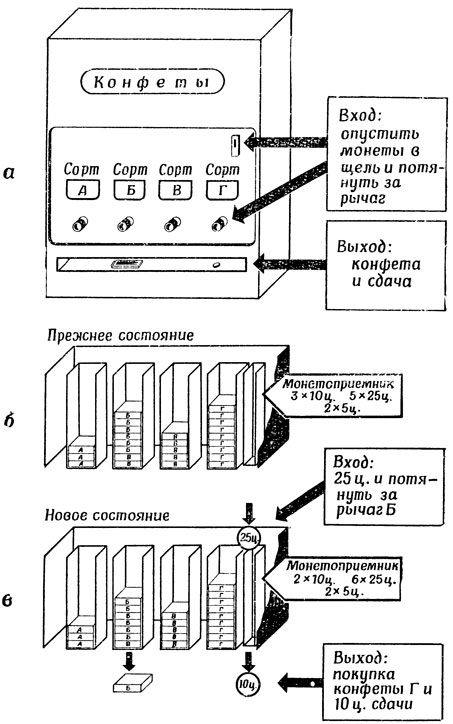
Рис. 33. Работа торгового автомата. а - вид автомата снаружи. Если опустить в щель монеты и потянуть за соответствующий рычаг, то на лоток выпадет покупка и сдача; б - внутренний вид автомата; в - внутреннее состояние: расположение конфет в каждом из четырех бункеров и набор сдачи. Как показывают рис. б и в, взаимосвязь между входом и выходом зависит от внутреннего состояния системы, и входные воздействия не только вызывают определенный выход, но и изменяют внутреннее состояние системы. (Вопрос: если для нового состояния автомата повторить вход '25 центов и потянуть за рычаг в', то каков будет следующий выход?)

Итак, описание любой реально существующей системы должно содержать следующие пять элементов, выбор которых в каждом конкретном случае будет зависеть от тех аспектов деятельности системы, которые нас интересуют.

1. Множество входов (входных воздействий): те изменяющиеся параметры окружающей среды, которые, как мы полагаем, оказывают влияние на интересующие нас аспекты поведения системы

2. Множество выходов (выходных величин): те параметры системы, которые мы наблюдаем либо просто потому, что они нас интересуют сами по себе, либо потому, что они, по нашему мнению, вносят существенные изменения во взаимоотношения системы и окружающей среды

3. Множество состояний: внутренние параметры системы (которые могут быть, а могут и не быть одновременно и выходными величинами), определяющие связь между входами и выходами. Состояние системы - это ее сконцентрированное прошлое; зная состояние системы, мы не нуждаемся ни в какой дальнейшей информации о том, что с ней было: это никак не уточнит наши предсказания о ее будущих реакциях на входные воздействия

4. Функция перехода состояния: определяет, как изменяется состояние системы при различных входах

5. Выходная функция: определяет выход системы при заданных входе и внутреннем состоянии

Мы еще раз подчеркиваем, что, хотя этой модели достаточно для объяснения поведения системы при известных входах в течение короткого промежутка времени, более тонкие теории, позволяющие объяснить более продолжительные взаимодействия, должны включать аналогичную модель и для окружающей среды. В качестве иллюстрации к этому положению рассмотрим систему А на рис. 34, а. Входами, выходами и состояниями для нее служат целые числа. Получив на входе число n, она независимо от своего состояния выдает на выходе n+1 и переходит в состояние (n+1). Таким образом, рассматривая эту систему изолированно, мы пришли бы к выводу, что она просто прибавляет единицу к любому числу, поданному на ее вход. Рассмотрим теперь систему A₁, которая является точной копией системы A, но работает теперь вместе с другой такой же копией A₂, с которой она связана так, как показано на рис. 34,б.

Теперь их функции представляются совершенно иными: система A₁ занимается тем, что выдает нечетные числа, а система A₂ - четные. Именно в этом смысле "целое есть больше, чем простая сумма его частей". Даже когда у нас есть полное представление о составных частях (рис. 34,а), мы не можем постигнуть самое существенное в их поведении, пока не объединим их (рис. 34,б).

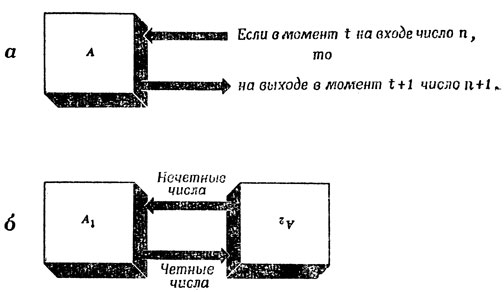
Рис. 34. 'Целое больше, чем сумма его частей'. Объяснения в тексте

Система, в которой функция перехода состояний и выходная функция однозначно по заданному начальному состоянию и заданной последовательности входных сигналов определяют новые состояния и выходы, называется детерминированной системой. И хотя именно такими системами мы и занимаемся в этой книге, необходимо заметить, что бывают случаи, когда, с какой бы точностью мы ни определяли последовательность входов, мы все равно не сможем с абсолютной уверенностью определить соответствующие состояния и выходы. Если нам повезет, то можно будет указать точные вероятности их появления - в этом случае у нас будет система, называемая стохастической.

Отметим коротко, что стохастический подход оправдывает себя, либо если мы проводим анализ системы на квантовом уровне, либо когда рассматривается макросистема, допускающая стохастическое описание в силу того, что мы решили пренебречь "тонкими деталями" взаимодействий на микроуровне.

Например, гораздо разумнее считать, что вероятность выпадения "решки" равна 0,5, чем учитывать начальное положение пальцев, силу толчка большим пальцем и т. п., пытаясь определить, как упадет монета в каждом конкретном случае. Аналогичным образом при анализе системы во многих случаях не имеет смысла подробно описывать ее входы или состояния, а гораздо полезнее описывать систему на достаточно грубом уровне, предполагающем измерения относительно небольшого числа переменных, с тем чтобы на их основе предсказывать лишь вероятности различных исходов.

Общепринятая интерпретация квантовой механики идет еще дальше и утверждает, что имеются вероятности, от которых нельзя освободиться, какими бы точными измерениями мы ни пользовались, и что в некотором смысле стохастичность - неотъемлемое свойство Вселенной. В ньютоновой физике состояние системы описывалось расположением ее элементов, которое можно наблюдать непосредственно, и их скоростями, которые можно вычислить, зная пройденные ими пути за известный промежуток времени. Понятие же состояния в квантовой механике становится гораздо более абстрактным. Здесь состояние - это так называемая волновая функция, которая задает лишь распределение вероятностей исходов на множестве наблюдаемых координат и скоростей. Интересно отметить, что, хотя в квантовой механике сам процесс изменения состояний во времени подчиняется детерминистическим закономерностям, знание состояния еще не позволяет делать точный прогноз, а лишь дает возможность определять вероятности различных исходов.

Многие психологи подходили к задачам обучения с позиций "стохастической теории обучения", предполагая при этом, что для мозга существуют лишь два возможных состояния: "обучен выполнению задания" и "не обучен выполнению задания", и что переход из одного такого состояния в другое осуществляется чисто стохастически. Конечно, реальные процессы обучения, происходящие в реальном мозге, складываются из громадного числа более тонких изменений, и лишь их результат допускает такую двоичную оценку, маскирующую непрерывность процессов в нервной системе. Это очень напоминает наш предыдущий пример с квантовой механикой, где состояние системы описывалось функцией, содержащей лишь информацию о распределении вероятностей результатов измерений. Никакой конечный набор измерений переменных квантовомеханической системы не может заменить эту бесконечную функцию, поскольку только она одна удовлетворяет требованиям, предъявляемым теорией систем к состояниям: "состояние содержит всю информацию о предыстории системы, обладающую тем свойством, что добавление какой-то новой информации никак не поможет уточнить предсказание о будущем поведении системы". Пытаясь описать работу мозга, мы должны будем ввести параметры состояния, столь же чуждые языку нынешней психологии, сколь чуждым было квантовомеханическое состояние для классических координат и скоростей ньютоновой механики. Конечно, ньютонова механика прекрасно подходит для исследования весьма широкого круга явлений. То же самое можно сказать и об обычной психологии. Но по мере того как расширяются возможности наблюдения, неизбежно выявляются и недостатки классических подходов.

Это положение хорошо иллюстрируют исследования ретикулярной формации (РФ) ствола головного мозга (рис. 2), которую мы рассмотрим подробнее в разд. 7.1; у млекопитающих РФ обеспечивает в основном сложные взаимодействия с высшими центрами мозга. Однако можно предположить, что у низших животных РФ частично служит механизмом "устранения избыточности потенциальных команд", направляющим весь организм на выполнение одной глобальной задачи; у высших животных РФ тоже несет среди прочего сходную функцию - регулирует чередование сна и бодрствования. Некоторые морфологические соображения заставляют предполагать, что локальные расчеты осуществляются в тонких дисках, расположенных по нормали к направлению спинного мозга, а каналы двусторонней связи между этими дисками, или "модулями", сосредоточены как раз в РФ. При этом каждый модуль получает разную сенсорную информацию. Возникает вопрос: как должно быть организовано взаимодействие этих модулей для того, чтобы могло вырабатываться общее решение, заставляющее животное перейти к выполнению того или иного действия? Килмер и Мак-Каллок предложили схему таких взаимодействий, которая в экспериментах на машинных моделях продемонстрировала удовлетворительные переключательные характеристики. В основу этой схемы был положен принцип, согласно которому каждая подсистема, используя свою частичную информацию, вырабатывает собственное пробное решение, которое в результате взаимодействия с другими подсистемами постепенно меняется до тех пор, пока не будет достигнута необходимая степень согласованности, на основании которой организм и станет действовать. И хотя внешне будет казаться, будто в каждый момент времени система осуществляет одну определенную программу действий, ни в какой момент времени такого описания не будет достаточно для того, чтобы понять динамику системы в целом.

Основываясь на этих положениях, обратимся к рис. 35, где схема нейронной сети рассматривается в терминах системного подхода. Одна из наших центральных проблем состоит в том, чтобы понять, насколько нейронные механизмы позволяют объяснить явления на психологическом уровне, ибо рассчитывать на простую редукцию в этом случае не приходится. Двум различным с психологической точки зрения стимулам - свету, движущемуся к субъекту, или неподвижному свету, к которому с той же относительной скоростью приближается субъект, - соответствуют идентичные нейронные входные воздействия, и отличаются они лишь по разнице внутренних состояний в этих двух случаях. Таким образом, на психологическом уровне входное воздействие зависит не только от нейронного входного воздействия, но и от внутреннего состояния на нейронном уровне. И наоборот, одну и ту же кнопку можно нажать многими разными способами, так что простого взаимно однозначного соответствия между нейронным и психологическим описаниями установить нельзя. Тем не менее мы покажем, что, несмотря на неприменимость наивной редукции, многие психологические явления можно объяснить на нейронном уровне.

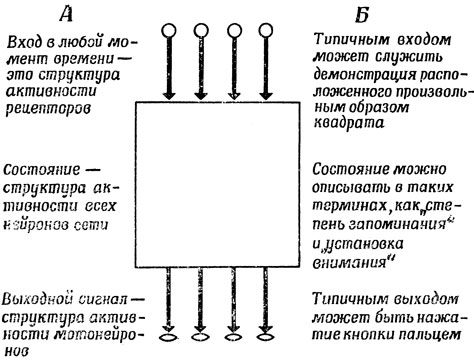
Рис. 35. Два вида описания сети в терминах параметров состояния: на уровне активности индивидуальных нейронов (А) и на уровне психологического описания (Б)

Рассмотрим теперь простую сеть из формальных "нейронов", которая поможет нам лучше почувствовать динамику системы, описываемой на нейронном уровне. Этот пример окажется полезным и для обсуждения иерархического устройства систем управления, которыми мы займемся в гл. 5. Он показывает, как просто осуществить на высшем уровне управление сетью, получая в результате необходимую последовательность действий. Рассмотрим в этой связи весьма упрощенную модель ноги, заимствованную у Вейса [252]; единственным шаровым суставом этой ноги управляют четыре мышцы.

Представим себе жесткую негнущуюся ногу, прикрепленную к суставу, как показано на рис. 36. Ногу можно выбросить вперед, сокращая отводящую мышцу (Ab), и назад - с помощью приводящей мышцы (Ad), ступня поднимается при сокращении поднимающей мышцы (El), а опускается при сокращении депрессора (De). Приведенная ниже последовательность мышечных сокращений несколько упрощенно показывает участие одной ноги в процессе движения четвероногого существа вперед. В начале цикла эта нога прочно стоит на земле и выдвинута далеко вперед относительно всего тела.

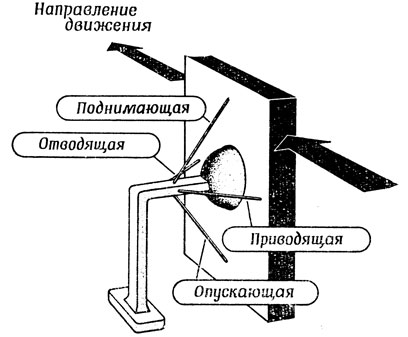
Рис. 36. Упрощенная модель ноги с шаровым суставом 'коленом'. Объяснения в тексте

Читателей, которых интересует более подробное описание процесса движения животных, мы отсылаем к работам рейса, [252], Робертса [215] и Грея [65]. Здесь же лишь отметим, что даже простая последовательность мышечных сокращений может привести к биологически полезному поведению.

Нетрудно, конечно, сконструировать нейронную сеть, которая может генерировать такую последовательность мышечных сокращений. Для упрощения схемы заменим мотонейронный пул, управляющий мышцей, одним формальным нейроном и изобразим дело так, как будто один-единственный импульс, поступающий в данный мотонейрон, заставляет соответствующую мышцу произвести сокращение необходимой продолжительности (рис. 37). Здесь (ср. с клетками на рис. 1) в момент времени t+1 в клетке возникает возбуждение, если в момент времени t на нее поступило воздействие через вход, у которого стоит 1, и не поступило воздействий через "отрицательные" входы.

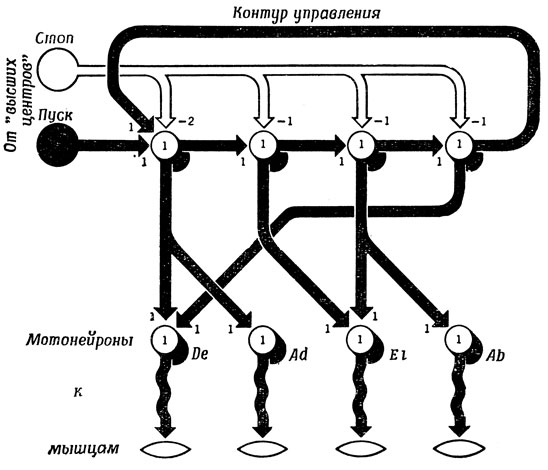
Рис. 37. Простая схема ритмического управления 'ногой', изображенной на рис. 36. Сигнал 'пуск' от 'высших центров' запускает импульс в замкнутом контуре, а сигнал 'стоп' прерывает активность контура

По сигналу "пуск", поступившему из "высших центров", в управляющем контуре начинает циркулировать импульс, а сигнал "стоп" прекращает в нем всякую активность. По мере того как четыре управляющих нейрона активируются циркулирующим импульсом, они вызывают необходимую последовательность мышечных сокращений. Таким образом, входом для этой схемы служит последовательность импульсов в двух входных каналах, идущих "от высших двигательных центров", а выходом - суммарная активность четырех выходных каналов, ведущих к мышцам. Однако очевидно, что вход сам по себе не определяет выход, если не уточнено состояние, т. е. последовательность импульсов, циркулирующих в контуре.

Упражнение. Преобразуйте эту схему так, чтобы сигнал "пуск" не мог вызвать новый импульс в управляющем контуре, если там уже циркулирует хотя бы один импульс, и чтобы задерживать действие сигнала "стоп" до тех пор, пока нога не будет стоять на земле.

Самое существенное в наших рассуждениях о состоянии нейронной сети заключается в том, что текущий выход системы ни в каком смысле не должен быть ответом на текущее входное воздействие, рассматриваемое в качестве стимула. Скорее наоборот, на возбуждение тех нейронов, которые определяют выход, может влиять активность нейронов системы, отражающая ее весьма далекую предысторию.

Последнее утверждение можно пояснить на очень простом примере (рис. 38). Рассмотрим формальный "нейрон" с двумя входами: одним внешним и другим, замкнутым на собственный выход. Значения параметров этой схемы подобраны так, что выход возбуждается в момент t+1, если в момент t возбужден тот или другой из этих входов. Предположим, что в начальный момент времени нейрон находится в состоянии покоя y(0)=0. Тогда до тех пор, пока не возбужден входной канал x, нейрон будет оставаться в состоянии покоя. Но как только x станет равным 1, возбудится канал y и в замкнутом контуре будет реверберировать импульс, обеспечивая спонтанное возбуждение нейрона. В результате такой нейрон навсегда "запоминает", что на него когда-то поступило входное воздействие.

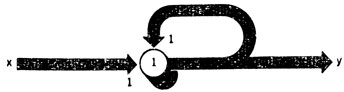
Рис. 38. 'Запоминающий' формальный нейрон. Он остается возбужденным 'навсегда'. Получив хотя бы одно входное воздействие благодаря тому, что в замкнутом контуре 'реверберирует' импульс обратной связи

Упражнение. Заметим, что ничего сверх этого он не може^т "запомнить". Подумайте, как добавить сюда еще один вход, который позволил бы возвращать этот нейрон в исходное состояние.

Продолжая обсуждать наш пример с рис. 38, можно представить себе, что вместо памяти, механизм которой основан на реверберации входного сигнала по замкнутому контуру, каждое возбуждение приводит к некоторому снижению порога; в результате при многократном возбуждении нейрона его порог в конце концов опустится до нуля, а сам он начнет возбуждаться спонтанно, независимо от входов. "Память" в этом случае заключена в пороговом значении и нечувствительна к сбоям, вызванным тем, что единственный импульс не смог по каким-то причинам пройти весь замкнутый контур.

Заметным ограничением предложенной выше модели системы является предположение, что функция перехода состояний определена раз и навсегда. На самом деле мы должны учитывать и то, что функция, задающая следующее состояние, может меняться во времени. Здесь уместен иерархический подход: на одном уровне и в одной временной шкале мы рассматриваем мгновенную деятельность системы, тогда как на другом уровне иерархии и в другой временной шкале, рассчитанной на более продолжительное время, мы видим, как меняются сами процессы, управляющие этой деятельностью. Стратегии такой адаптации мы рассмотрим в разд. 3.4.

Для описания того, как система, подобная мозгу, адаптируется во времени, можно было бы ввести пространство состояний огромной размерности и учесть не только состояние, управляющее текущей деятельностью, но также и состояние, определяющее процессы адаптации и обучения. Однако такое многообразие состояний лишь затемняет существо вычислительного процесса, который можно было бы обнаружить, рассматривая пространство состояний меньшей размерности и соответствующее ему поведение и предполагая, что динамика поведения в этом пространстве сама меняется во времени. Когда мы исследуем систему как адаптивную, то обычно предполагаем, что имеется детерминированная система, состояние которой несложно разбить (рис. 39) на две составляющие: одну, меняющуюся сразу, ту, которую мы не вполне точно называем "состоянием", и другую, меняющуюся медленно, о которой мы говорим как о параметрах адаптации системы. На языке психологии это называется кратковременной (оперативной) и долговременной памятью.

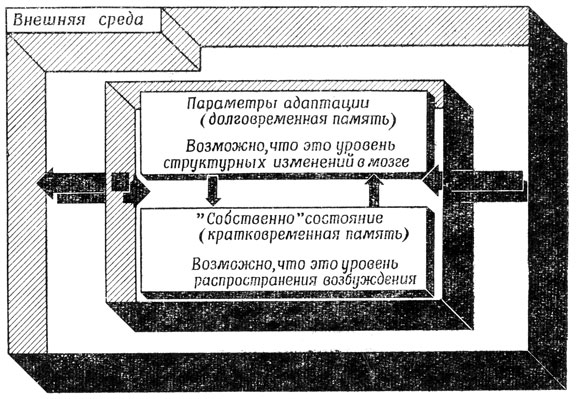
Рис. 39. Функциональная декомпозиция адаптивной системы на подсистемы двух уровней: 'долговременную' и 'оперативную' память (ср. с рис. 48)

Такая декомпозиция может значительно способствовать пониманию функции системы. Впрочем, одновременно с этим она может привести и к совершенно ошибочному представлению о ее структуре. Например, "собственно состояние" нейронной сети может задаваться структурой импульсного ответа нейронов, а параметры адаптации - распределением синаптических весов и порогов тех же самых нейронов. Поэтому (ср. с рис. 1) отнесение этих двух параметров к двум разным системам может не иметь никакого физического смысла, но зато может оказать нам помощь в понимании связанных с ними психологических процессов и привести к полезной математической модели для изучения функционирования системы. При этом ничто не заставляет нас ограничиваться только двумя уровнями.

Некоторые психологи различают кратковременную и долговременную память потому, что последняя не исчезает и после того, как возбуждение в нейронной сети прекратится. Сейчас мы коротко остановимся на экспериментах, подтверждающих правомерность такого деления. Затем в разд. 3.4 мы на основе нашего простенького примера регулирования параметров (рис. 38) коснемся задачи идентификации в теории управления, где от регулятора требуется скорректировать значения параметров, используемых им для управления некоторой другой системой.

В нейронных сетях, приведенных на рис. 37 и 38, состояние системы было закодировано в виде активности формальных "нейронов". Если бы эта активность оказалась прерванной, то соответствующие системы потеряли бы память при условии, что в них не предусмотрен какой-то другой механизм запоминания вроде снижения порога, гипотетически предложенного для схемы на рис. 38. Известны экспериментальные подтверждения того, что "хранение информации" в оперативной памяти связано с электрической активностью мозга, тогда как долговременную память обеспечивают совсем другие механизмы. Здесь мы ограничимся кратким описанием трех старых опытов. Множество подобных экспериментов описано Джоном [128] и Гуровицем [96]. Здесь достаточно сказать, что слишком многие из них свидетельствуют о необходимости настоящего кибернетического подхода, который должен сменить наивное представление о памяти как о регистрации некоторого числа пар стимул - реакция с помощью уже готовых синапсов на представление о ней как об одном из средств обеспечения адаптации организма к характеристикам сложной внешней среды.

Воспользовавшись тем фактом, что у хомяков можно искусственно вызвать зимнюю спячку, Рансмейер и Джерард [211] обучили животных эффективному поведению в лабиринте, а затем охладили их до температуры 5°С, практически подавив электрическую активность нейронов. Затем хомяков отогрели до нормальной температуры и снова предложили им лабиринт. Не было замечено никакой потери памяти. На этой основе Рансмейер и Джерард сделали вывод, что запоминание информации связано с какими-то химическими изменениями, а не с электрической активностью.

Другие эксперименты наводят на мысль, что электрическая активность может играть роль как в формировании оперативной памяти, так и для "перезаписи" информации в долговременную память, и были попытки измерить время, необходимое для такого закрепления информации.

Дункан изучал влияние электросудорожного шока (ЭШ)^*, который применяют для нарушения у крыс текущей электрической активности при обучении. В эксперименте использовали ящик с двумя одинаковыми отсеками. В одном из отсеков пол был решетчатым и по нему можно было пропускать ток. Другой отсек был выкрашен в белый цвет и в нем горела 100-ваттная лампа, так что внешне первый отсек казался крысам более безопасным. После того как крыса осматривала оба отсека и возвращалась в отсек с решетчатым полом, через решетку пропускали разряд, достаточно сильный, чтобы заставить крысу перебежать в другой отсек. Животное оставляли там в течение 10 секунд, а затем вынимали и после определенного времени применяли ЭШ. Эксперимент проделали с несколькими крысами, варьируя интервал между ударом тока на решетке и ЭШ.

^* (Электрошоковую терапию, применяемую в психиатрии, можно сравнить с ударом по забарахлившему механизму; и то и другое предполагает полное незнание глубинных механизмов, но иногда дает результаты.)

Процедуру повторяли, давая крысам 10 секунд, чтобы перейти с решетки в безопасный отсек до того как будет пропущен ток, и наблюдали, насколько хорошо крысы научились избегать удара током. У крыс, которые получали ЭШ с интервалом не больше 4 минут, наблюдалась значительная потеря памяти: они не умели избежать удара током, удрав в освещенный отсек. Если же интервал составлял час и более, то никакой разницы в поведении крыс получивших ЭШ, и контрольных животных, не получавших ЭШ, не отмечалось.

Это наводит на мысль, что время консолидации при переходе информации из оперативной в долговременную память составляет от 4 минут до одного часа. Однако на это можно возразить, что ЭШ вовсе не разрушает оперативную память, а просто показывает зверьку, что удар током в первом отсеке в конце концов не так уж и страшен! Парируя эти возражения, Куортермейн [206] провел следующий эксперимент. Крысу помещали в тесный лифт, который затем опускали к земле; в этот момент крыса обычно выпрыгивала и получала в наказание удар током. Если в течение не более чем 15 секунд после этого крысу подвергали ЭШ, то при повторном испытании она чаще всего снова выпрыгивала. Куортермейн провел серию таких опытов, помещая крыс в черные мешки, чтобы у них не выработалось реакции избегания к тому месту, где они получают ЭШ. Поведение этих крыс по существу не отличалось от поведения остальных. Это подтверждает теорию, что разрушение информации после ЭШ обусловлено настоящей амнезией, вызванной физиологическими изменениями, а не помехами обучения. Как согласовать 15-секундное время консолидации в опытах Куортермейна с 15-минутным интервалом, наблюдавшимся Дунканом, остается неясным. Другие опыты (описанные в книгах, на которые мы ссылались выше) показывают, что еще более длительные помехи возникают при применении химических веществ, нарушающих биохимические процессы, происходящие в клетках. Это просто говорит о том, что между кратковременной и долговременной памятью нет четкой границы, а одна форма постепенно переходит в другую. Остается надеяться, что создание достаточно изощренных моделей структуры памяти, возможно даже в направлениях, намечаемых нашей кассетной метафорой (разд. 4.1), приведет к новым концепциям, которые можно будет положить в основу критического эксперимента.