3.3. Обратная связь

Скомандовав роботу повернуться на 30°, для чего он должен зафиксировать положение одного колеса и повернуть другое на 6 оборотов, мы можем рассчитывать на успех лишь при условии, что ни одно из колес, например, не пробуксует. В противном случае управляющему устройству, или регулятору, придется передать роботу команды о дополнительных маневрах, необходимых для того, чтобы перевести его в требуемую позицию. Аналогичным образом, управляя взаимодействием системы с внешней средой, при котором всегда возможны непредвиденные возмущения, совершенно необходимо непрерывно передавать информацию от периферических рецепторов обратно регулятору, и эта информация сообщает ему, насколько эффективно он управляет осуществляемым взаимодействием.

Например, человеку гораздо проще схватить движущийся предмет, если он видит, насколько нужно вытянуть руку, т. е. если мозг обладает зрительной обратной связью от рецепторов (в данном случае от глаз) к эффектору (в данном случае к руке). Мозг сможет подобрать необходимые команды мышцам, чтобы сократить разницу между истинным и желаемым положением руки. Или еще: во время ходьбы мы существенным образом используем "обратную связь" от рецепторов глубокой чувствительности, воспринимающих давление пола на подошвы ног, в чем прекрасно мог убедиться каждый из нас на собственном опыте: когда нога "немеет" и приходится ступать без такой обратной связи, движения наши становятся неловкими и плохо координированными.

Подобная обратная связь, т. е. сравнение того, что действительно происходит, с тем, чего бы мы хотели, должна играть важную роль при управлении организмом или роботом. Общая схема системы управления с обратной связью приведена на рис. 41.

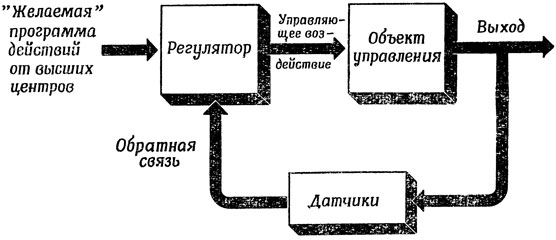
Рис. 41. Общая схема системы, использующей для вычисления управляющего воздействия обратную связь, по которой поступает информация о текущем состоянии управляемого объекта

Регулятор, имеющий возможность постоянно контролировать результаты предыдущих управляющих воздействий, может их изменять, если результирующее поведение системы в какой-то мере неудовлетворительно, скажем, из-за неожиданных возмущений окружающей среды. Например, управляя автомобилем, - можно, несмотря на различия в наклоне дороги, поддерживать - определенную скорость, если мы по спидометру определяем, что нужно сделать в данный момент - "прибавить газу" или притормозить.

На рис. 42 мы изобразили частный случай обратной связи - так называемую отрицательную обратную связь, где через θ_d обозначено желаемое значение выходного сигнала, а через 0а - результат измерения истинного значения этой величины; они поступают в детектор ошибок, где вычисляется разность

e=θ_d-θ_a

и этот сигнал ошибки подается в регулятор. Для каждой такой конкретной системы задача состоит в том, чтобы построить регулятор, уменьшающий погрешность е до достаточно низкого" уровня.

Предположим теперь, что регулятор работает неправильное в результате чего возникает перекомпенсация этой ошибки. Другими словами, если в начальный момент времени ошибка е была положительной, то такой регулятор "исправляет" ее на отрицательную, но еще большей величины. Естественно, что в следующий момент времени эта новая ошибка будет "исправлена" на еще большую, только положительную, и так до бесконечности, в результате чего в системе возникнут нарастающие колебания^*. Поэтому, конструируя регулятор, мы должны заботиться о том, чтобы получающаяся в результате система была устойчивой и чтобы при относительно постоянном входном воздействии ее сигнал ошибки достаточно быстро снижался до нуля.

^* (У читателя не должно создаваться впечатления, что для успешной работы регулятора необходимо, чтобы он сразу полностью исправлял ошибку. Действительно, в системе, где регулятор "исправляет" исходную ошибку на ошибку другого знака, но меньшей абсолютной величины, также возникают колебания, но они будут затухающими и постепенно ошибка станет сколь угодно малой. Такие колебания тоже могут быть нежелательны для некоторых систем, но в любом случае они гораздо "приятнее" нарастающих. Аналогично обстоит дело с системами, регулятор которых вызывает недокомпенсацию ошибки, т. е. вносит коррекцию, уменьшающую ошибку по величине, но не меняющую ее знака. В такой системе сигнал ошибки тоже затухает, да и колебаний, хотя бы и затухающих, в ней нет. Возможность обойтись без точной компенсации и составляет самую суть использования обратной связи. - Прим. перев.)

Систему с отрицательной обратной связью, подобную приведенной на рис. 42, часто называют следящей. И именно системе управления корабля (а это типичная следящая система) мы обязаны термином "кибернетика", так как этимология этого термина берет свое начало от греческого слова "кибернетек", что означает "кормчий". Как мы уже видели, одно из важных свойств следящей системы состоит в том, что при неудачной конструкции в ней могут возникнуть нарастающие, а не затухающие колебания. И одно из прозрений Норберта Винера, заложившее основу его труда "Кибернетика", состояло в том, что именно подобными нарушениями обратной связи можно объяснить некоторые заболевания человека.

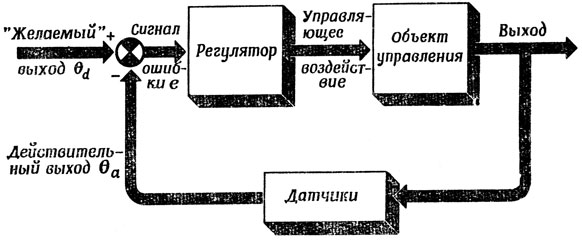
Рис. 42. Система с отрицательной обратной связью, использующая для управления сигнал ошибки e=θ_d-θ_a, т. е. разность между желаемым состоянием объекта управления и его текущим состоянием

Например, на основании анализа систем с обратной связью Винер смог предсказать два типа нарушений, встречающихся у человека. А его друзья-клиницисты подтвердили существование двух заболеваний, соответствующих этим нарушениям. При одном заболевании человек не может стоять выпрямившись с закрытыми глазами и с большим трудом ходит, так как ему все время нужно смотреть на ноги, которые он поочередно выбрасывает вперед. Это заболевание называется сухоткой спинного мозга; оно сопровождается патологическим процессом в спинном мозгу, в результате которого центральная нервная система не получает сигналов обратной связи от суставов, сухожилий, мышц и опорных поверхностей ступней ног. При другом заболевании человек кажется здоровым, пока ничего не делает, но стоит ему, например, попытаться взять стакан с водой, как его рука начинает дрожать и дергаться так сильно, что он расплескивает воду, не донеся ее до рта. Спинальная система обратной связи такого пациента не нарушена, но у него поврежден мозжечок, и, по-видимому, это повреждение приводит к недостаточному торможению мышечной активности, а это в свою очередь - к неустойчивым колебаниям, проявляющимся в виде тремора при выполнении произвольных движений.

Эти примеры позволяют нам убедиться в том, что одного лишь наличия обратной связи еще недостаточно и что для обеспечения плавного координированного поведения эта обратная связь не должна быть ни слишком сильной, ни слишком слабой.

После того как мы продемонстрировали важность обратной связи для задач управления, хотелось бы подчеркнуть, чта в теории мозга нас будут интересовать системы, для которых сигналами служат не отдельные числа, а целые комплексы активности. Чтобы стало понятным, что мы при этом имеем в виду, займемся вкратце системой управления движениями глаз (этот вопрос более тщательно рассмотрен в гл. 7); это послужит фундаментом для изучения более общих схем управления с обратной связью, теория которых развита на основе работы Питтса и Мак-Каллока [202].

Многие авторы, пытавшиеся применить теорию управления для моделирования фиксации взгляда на неподвижном или медленно движущемся объекте, отмечали, что основную роль в этой системе играют два параметра: текущее направление взгляда θ и требуемое направление θ_d. После того как это было установлено, они пытались проанализировать поставленную задачу в терминах системы управления, схема которой приведена на рис. 43, при этом они задавали себе вопрос, какую функцию от θ и θ_d нужно вычислить, чтобы определить угловое ускорение глаза θ.

Подобный подход приводил к успеху при анализе многих биологических систем, но он может оказаться совершенно непригодным там, где речь идет о деталях нейронной сети, так как в нем скрыто представление о мозге как о руководителе централизованной системы, манипулирующем небольшим числом данных, например θ и θ_d, отдающем директивы о необходимом значении θ.

Однако мозг не получает значения θ_d в готовом виде; она закодировано в спайках активности целого слоя нейронов, в палочках и колбочках глаза. Кроме того, для управления движениями глаза недостаточно одного сигнала управления, несущего значение θ, поступающего на поворачивающий глазное яблоко исполнительный механизм; для этого нужно возбудить по крайней мере одну пару мышц-антагонистов, но даже для этого недостаточно двух сигналов, так как каждая мышца - это целая группа волокон, и для того чтобы она сократилась, необходима координированная активность целой популяции мотонейронов.

Поэтому, хотя и можно представить себе, как построить робот, "мозг" которого будет сконструирован по схеме централизованного преобразователя (θ_d, θ)→θ (рис. 43), понадобится специальное устройство предварительной обработки данных, которое играло бы роль "воронки", собирающей в одно число θ_d всю совокупность сигналов об активности сетчатки.

В действительности такая схема может оказаться полезной для робота, предназначенного для того, чтобы отслеживать одиночные цели, а не взаимодействовать со сложной средой, и имеющего в качестве эффектора только одно исполнительное устройство, для которого значение θ является подходящей командой управления. Однако если выходной сигнал нужно "разыграть" на целой системе мотонейронов, как это имеет место в биологии, прежде чем в результате сложных преобразований мы получим θ, так сказать, "в упакованном виде", то полезность централизованного процессора начинает внушать самые серьезные сомнения.

Для того чтобы сохранить особенности параллельной обработки информации, мы должны прежде всего представить себе преобразования, которым могут подвергаться целые комплексы данных. Найти знакомые примеры таких преобразований совсем не трудно. В самом деле, все мы видим, что три фигуры, изображенные на рис. 44, - это квадраты, хотя они различаются по своим размерам, ориентации и расположению. Как мы выясним ниже, изменения, необходимые для того, чтобы превратить один из этих квадратов в другой, принадлежит одной группе преобразований (нам придется сейчас немножко заняться математикой). Даже читателям, не склонным к занятиям математикой, принесет некоторую пользу ознакомление с излагаемым здесь материалом, хотя детальный разбор его совершенно не обязателен для понимания дальнейшего изложения.

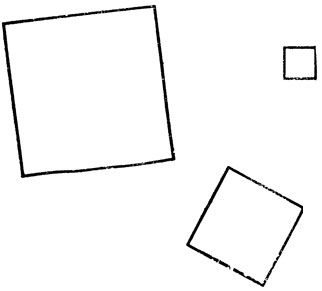
Рис. 44. Квадрат всегда квадрат всегда квадрат

Рассмотрим прежде всего, как можно передвигать фигуры по плоскости, не поворачивая их и не меняя их размеров. В этом случае каждая точка фигуры проходит одинаковый путь, и этот сдвиг можно описать величиной и направлением вектора, соединяющего прежнее и нынешнее положение каждой точки.

Обозначим тогда через T_α перенос фигуры, при котором каждая точка сдвигается на вектор а, как показано на рис. 45.

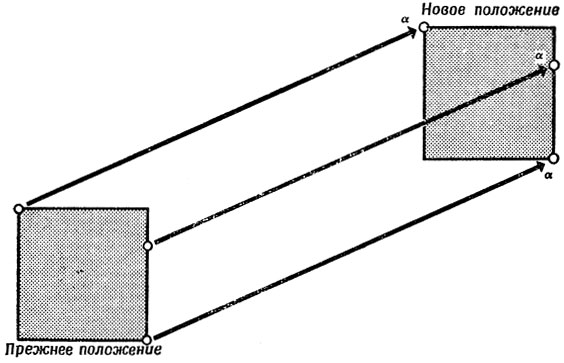
Рис. 45. Перенос T_α квадрата, задаваемый вектором

Очевидно, что если α - это вектор нулевой длины, α=0, то при соответствующем переносе T₀ каждая фигура останется там же, где она была до этого. Поэтому перенос T₀ называется тождественным или единичным.

Если нам задана пара переносов T_α и T_β, то мы можем выполнить сначала перенос T_α, а затем T_β и получим составной перенос T_β•T_α. ("Обратный" порядок этой записи объясняется тем, что мы обозначаем через T_φ результат воздействия преобразования T на фигуру φ, а тогда преобразование, переводящее φ в T_β(T_αφ), следует обозначить T_β•T_α.) Как видно из рис. 46,А, преобразование T_α-T_β совпадает с переносом T_α+β, определяющимся суммой векторов, задающих исходные преобразования. Другой рисунок, рис. 46,Б, показывает, что безразлично, осуществить ли сначала составной перенос T_β•T_α, а затем уже перенос T_γ или сначала выполнить перенос Tα, а затем осуществить составной перенос T_γ•T_β. И то и другое приведет к одинаковому результату, т. е.

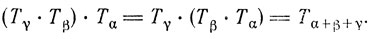
Наконец, рис. 46, В показывает, что если произвести сначала перенос T_α, а затем T_-α, т. е. перенос на то же расстояние, но в противоположном направлении, то один из этих переносов "уничтожит" эффект другого, т. е.

Преобразование T_-α называют обратным по отношению к T_α, и его часто обозначают через T_α^-1, где верхний индекс указывает на переход к обратному преобразованию.

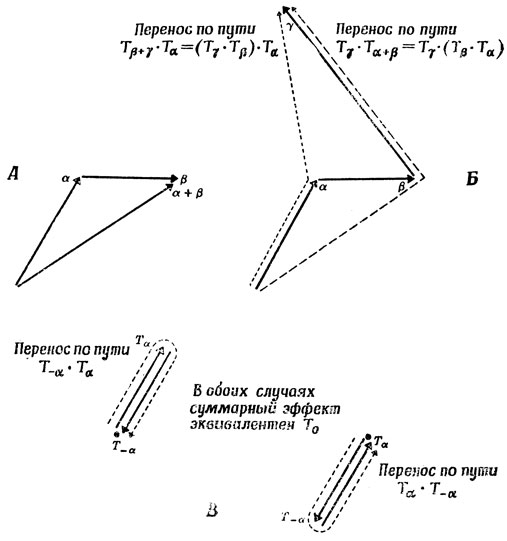
Рис. 46. А. Если за переносом T_α следует перенос T_β, то получается перенос T_α+β Б. Ассоциативность: последовательность переносов T_α, затем T_β, затем T_γ приводит к одинаковому результату независимо от того, как сгруппировать эти три переноса. В. Каждому переносу T_α соответствует обратный перенос T_-α, компенсирующий эффект первого и приводящий к тождественному или единичному преобразованию (без каких-либо изменений) T₀^-

Таким образом, на множестве всевозможных переносов на плоскости определен закон композиции, ставящий в соответствие любой паре переносов T_α и T_β перенос T_α+T_β, и имеется тождественное или единичное преобразование T₀, а для каждого переноса T_α определен обратный ему T_-α. Наконец, любая тройка переносов удовлетворяет так называемому закону ассоциативности:

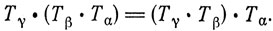
Поэтому множество переносов может служить примером того, что математики называют группой.

Определение. Группой называется множество G с определенной на нем операцией, ставящей в соответствие любой паре g₁ и g₂ элементов из G некоторый третий элемент g₁•g₂ этого же множества и удовлетворяющей следующим условиям:

1. Операция, определенная на множестве, ассоциативна, т. е. для любых трех элементов g₁, g₂ и g₃ множества G справедливо равенство

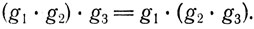
2. Множество G содержит единичный элемент, т. е. такой элемент, что для любого g из G выполняется равенство

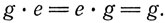
3. Каждому g из G соответствует обратный ему элемент g^-1, причем

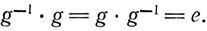
Например, множество обычных неотрицательных чисел с определенной на нем операцией сложения не является группой, поскольку обратными относительно этой операции элементами должны быть отрицательные числа. Аналогично всевозможные целые числа не образуют группы относительно операции вычитания, так как в этом случае не выполняется закон ассоциативности: если c≠0, то

Возвращаясь к преобразованиям, сохраняющим свойство фигур "быть квадратом", мы увидим, что группу образуют не только переносы, но и преобразования подобия, т. е. преобразования, приводящие к изменению масштаба фигуры в k раз (где k>0). В этом случае единичным преобразованием служит подобие с коэффициентом подобия k=1, не меняющее размеров фигур, а обратным относительно подобия с коэффициентом k служит подобие с коэффициентом 1/k. Образуют группу и повороты. [А как по-вашему, что служит единичным преобразованием в этом случае? А обратным по отношению к заданному?]. Читатель, знакомый с евклидовой геометрией, может быть, помнит, что две фигуры называются конгруэнтными, если можно получить одну из другой с помощью "конгруэнтных преобразований", т. е. вращений и переносов, и называются подобными, если допустимая группа преобразований включает в себя не только вращения и переносы, но и преобразования подобия. Великому математику XIX в. Ф. Клейну принадлежит мысль, что любую геометрию (как евклидову, так и неевклидову и даже топологию) можно рассматривать как изучение тех свойств фигур, которые инвариантны относительно некоторой заданной группы преобразований.

С этих позиций вполне естественно заняться поиском сетей, выходные сигналы которых определяются лишь свойствами входа, инвариантными относительно некоторой заданной группы операций G. Рассматривая одну из схем, которая, быть может, лежит в основе нашей способности узнавать зрительные образы, несмотря на такие их преобразования, следует подчеркнуть очень важное обстоятельство, связанное с рис. 44: как бы мы ни смотрели на изображенные там фигуры, даже если мы станем рассматривать их по одной, различия в характере стимуляции сетчатки будут гораздо значительнее, чем сходства. Поэтому необходима дальнейшая обработка сигналов после рецепторов, направленная на извлечение этого сходства.

Питтс и Мак-Каллок [202] предложили схему, позволяющую найти преобразование T из множества G, приводящее образ φ к стандартному виду φ₀=T_φ. (В разд. 7.3 мы столкнемся со случаем, когда пользуются и преобразованиями выходной активности для того, чтобы привести зависимость между входом и выходом к стандартной форме.)

В работе Питтса и Мак-Каллока искомое преобразование находилось в два этапа.

1. Каждому образу φ сопоставлялся "вектор ошибки" E(φ), который обращался в нуль тогда и только тогда, когда φ оказывался в стандартной форме.

2. В зависимости от вида вектора ошибки E(φ) выбирается преобразование W, обладающее свойством уменьшить ошибку. Другими словами, для любых образов φ мы требуем, чтобы вектору ошибки E(φ) ставилось в соответствие такое преобразование W[E(φ)], что ошибка преобразованного W[E(φ)] образа φ оказывается меньше, чем для φ:

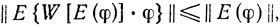
причем выписанное выше нестрогое неравенство становится равенством только при E(φ)=0. В дальнейшем мы станем обозначать W[E(φ)] через W_φ.

Основная задача построения такой схемы состоит в том, чтобы найти подходящую меру ошибки E, и преобразование W, которое, используя этот сигнал ошибки как обратную связь, может необходимым образом управлять системой и в конце концов свести ее ошибку к нулю, т. е. привести исходный образ к стандартному виду.

Подобная схема с обратной связью может быть реализована двумя основными способами, причем Питтс и Мак-Каллок явно рассмотрели лишь один из них.

В баллистической схеме структура W такова, что ошибку удается свести к нулю за один шаг, т. е. в этом случае

E(W_φ•φ)=0,

каково бы ни было φ.

Таким образом, управление в этом случае осуществляется следующим образом:

1) по заданному φ вычисляется E(φ), а следовательно, и W_φ;

2) вычисляется W_φ•φ=φ;

3) предполагается, что φ и есть стандартная форма.

Именно такую схему применяют в баллистике, где роль E(φ) - это отклонение пули от цели, а W_φ определяется наводкой в момент выстрела, поскольку вносить коррекции на промежуточных участках траектории нельзя. И в этом принципиальная разница между снарядом и управляемой ракетой, траекторию которой можно многократно корректировать.

В схеме слежения не обязательно, чтобы первоначальная ошибка E(W_φ•φ) исправлялась сразу; достаточно, если после коррекции она стала хоть сколько-нибудь меньше, чем E(φ). Мы требуем только, чтобы в результате многократной коррекции, основанной на использовании обратной связи, эта ошибка стремилась к нулю. Управление, реализующее такую стратегию слежения, может быть построено одним из двух следующих способов: 1) непрерывно изменяют образ до тех пор, пока он не приведется к стандартной форме; 2) непрерывно изменяют преобразование, пока не получат преобразование, сразу приводящее исходный образ к стандартному виду.

Приведем соответствующие программы.

I. Пусть φ - результат последнего преобразования входного образа.

1. Заменить φ новым входным образом.

2. Вычислить E(φ) и найти W_φ.

3. Вычислить новый образ φ в виде W_φ•φ.

4. Достаточно ли мало E(φ)?

ДА: стоп, φ в стандартной форме.

НЕТ: переходите к команде 2.

II. Пусть T - последний вариант преобразования, а φ фиксировано.

1. Выбрать начальное значение T, положив его равным тождественному преобразованию I•φ=φ.

2. Вычислить E(T_φ) и найти W[E(T•φ)].

3. Вычислить новое T в виде W[E(T_φ)]•T.

4. Достаточно ли мало новое E(T_φ)?

ДА: Стоп, T_φ в стандартной форме.

НЕТ: переходите к команде 2.

Для обеспечения сходимости этих программ необходимо условие, более строгое, чем (1). Например, можно потребовать, чтобы при некотором δ из интервала (0,1) и при любых возможных φ выполнялось неравенство

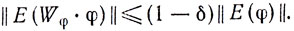
Тогда сходимость предложенных программ следует из того, что (1-δ)ⁿ→0 при n→∞.

На рис. 47 приведена схема системы с дискретным временем, реализующая программу II и генерирующая для каждого φ преобразование T_φ, приводящее его к стандартной форме.

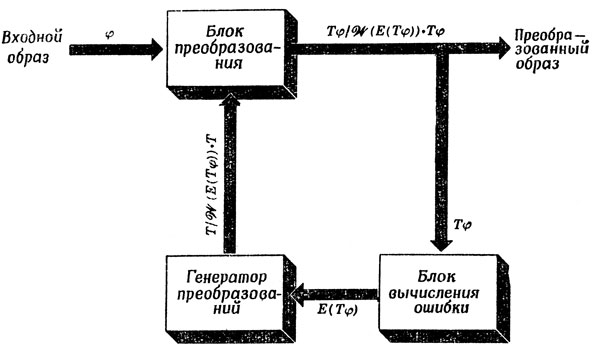
Рис. 47. Обобщенная схема Питтса - Мак-Каллока для преобразования зрительных образов к стандартному виду. Обозначение T/W на стрелках означает, что если в момент t в этом канале сигнал был равен T, то в момент t+1 он будет равен W

Блок, вычисляющий результат преобразования образа, в этой схеме не имеет памяти: принимая на вход образ φ и преобразование T, он однозначно выдает на выходе преобразованный образ T_φ. Нет памяти и у блока вычисления ошибки: образ φ на входе этого блока однозначно определяет ошибку E(φ). А вот генератор преобразований является детерминированной системой: если в момент времени t его состоянием было преобразование T, а на входе был вектор ошибки e, то в момент времени t+1 и состояние его и выход будут равны W(e)•T.

Возможны приложения, в которых разумно применять смешанную стратегию, сочетающую в себе свойства баллистической стратегии и стратегии слежения. Например, использовать сначала генератор W₁ для того, чтобы сделать "большой скачок" и подвести исходный образ достаточно близко к стандартному виду, а затем перейти к использованию генератора W₂, работающего по принципу слежения, и уже с его помощью осуществить "тонкую подстройку" образа к окончательному стандартному виду. В гл. 5 мы выскажем предположение о том, что именно такие "смешанные" стратегии лежат в основе "принципов организации" ЦНС.