3.4. Адаптация

Сущность теории управления составляет следующая задача: "Располагая достаточно точным описанием системы и зная, что от нее требуется, найти такие воздействия, которые, будучи поданы на вход системы, обеспечат желаемое поведение (или разумное приближение к нему)".

Обычно ситуация осложняется тем, что характеристики системы, которой мы собираемся управлять, известны недостаточно точно и могут даже меняться во времени. Например, одно из наиболее интригующих свойств мозга животного в процессе роста состоит в том, что он должен уметь (и умеет) управлять телом, которое со временем не только увеличивается в размерах, но и изменяет свои пропорции. Кроме того, внешние объекты с фиксированными свойствами изменяют эти свои свойства по отношению к организму и мозг должен многократно приспосабливаться к этому. Таким образом, приспосабливаясь ли к росту тела или обучаясь взаимодействию с новыми объектами в окружающей среде, мозг должен постоянно решать то, что в теории управления называют задачей идентификации: "С помощью достаточного числа экспериментов, сводящихся к наблюдению за реакцией некоторой системы на известные входные воздействия, построить динамическую модель системы, обладающую аналогичным поведением".

Для теории управления процедуры идентификации очень важны. Например, представьте себе, что нужно управлять системой, динамические уравнения которой неизвестны. Тогда вместо того, чтобы конструировать регулятор, пригодный для управления лишь одной специфической системой, построим универсальное управляющее устройство, которое после регулировки некоторых своих параметров сможет управлять любой системой из достаточно широкого множества, причем отрегулированные значения параметров должны соответствовать значению параметров управляемой системы. После этого мы не станем подсоединять такое управляющее устройство непосредственно к объекту, а предварительно воспользуемся процедурой идентификации. (Возможности использования такой схемы при управлении движениями в мозжечке рассматривались Бойллзом и Арбибом [30].) В этом случае регулятор будет все время работать, основываясь на тех значениях параметров управляемой системы, которые доставляются ему системой идентификации в качестве наилучших из числа возможных в данный момент времени оценок (рис. 48).

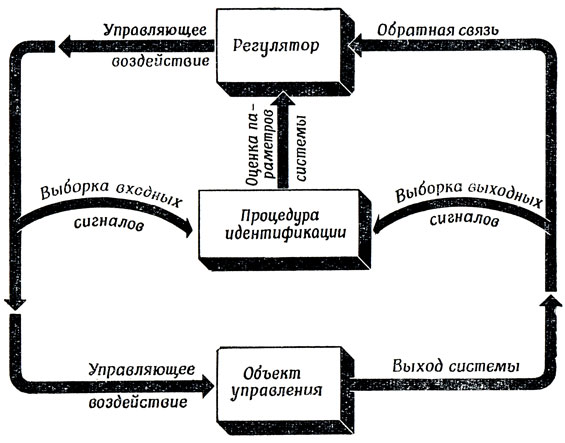
Рис. 48. Регулятор, использующий оценки параметров объекта, полученные с помощью процедуры идентификации, для того чтобы лучше управлять объектом управления (ср. с рис. 39)

Если параметры управляемой системы меняются во времени относительно медленно и процедура идентификации успевает Дать достаточно точные оценки параметров системы раньше, чем они изменятся, то такой регулятор будет работать хорошо, несмотря на флуктуацию динамических свойств управляемой системы. Управляющее устройство вместе с процедурой идентификации как раз и представляет собой то, что принято называть "адаптивным регулятором" - он адаптируется (т. е. приспосабливает свою стратегию управления) к изменениям динамики объекта управления.

Заметим, не останавливаясь на этом подробнее, что в ряде случаев бывает необходимо, чтобы процедура идентификации генерировала некоторые входные воздействия и для объекта управления, т. е. посылала на его вход сигналы - тесты для проверки различных гипотез о значениях его параметров. В этом случае придется искать компромисс между снижением качества управления вследствие того, что мы не располагаем достаточно точными оценками параметров управляемой системы, и снижением качества управления, .связанным с тем, что регулятор время от времени передает управление объектом процедуре идентификации.

Другими словами, "мозг" (т. е. регулятор + процедура идентификации) взаимодействует с "внешней средой" (включая и собственное тело, а не только внешние объекты), используя для этого внутреннюю модель (описываемую самым последним набором параметров адаптации), и это взаимодействие должно обеспечивать коррекцию внутренней модели, а также изменение взаимоотношений с внешним миром в желаемом направлении.

Теория управления оказалась в состоянии предложить некоторые алгоритмы идентификации, позволяющие на основании наблюдений за относительно простым внешним поведением системы находить компактное описание ее внутренних процессов. Однако необходимо помнить, что эти алгоритмы эффективны только тогда, когда "размерность" системы довольно мала. Нам много еще придется заниматься теорией, прежде чем мы найдем такие глобальные параметры состояния организма, которые дают возможность воспользоваться этими алгоритмами или приближенными методами, позволяющими исследовать системы, не вдаваясь во все их сложности. В то же время перед экспериментаторами стоит задача отыскать такие интересные для нас подсистемы, для которых возможно точное и строгое использование существующего теоретического задела.

Для того чтобы продемонстрировать, как процедуры идентификации могут помочь в управлении системой, например помочь мозгу управлять необыкновенно сложными взаимодействиями с внешним миром, расскажем в общих чертах о процедуре идентификации, использованной Сэмюэлом [221] в его ранних работах по составлению программ игры в шашки. Поскольку никто не знает точных рецептов, следуя которым можно наверняка выиграть при игре в шашки, Сэмюэл составил программу так, чтобы вычислительная машина просматривала последствия каждого хода на несколько ходов вперед и на основании этого выбирала наилучший ход. (В программу были заложены также некоторые правила сокращения перебора ходов, для которых нужно вести расчет, потому что даже машина, способная выполнять миллионы операций в секунду, может испытывать недостаток времени. Эти правила имеют прямое отношение к методам эвристического поиска, о которых мы будем говорить в разд. 4.2.)

Таким образом, стоявшая перед Сэмюэлом задача заключается в том, чтобы найти для вычислительной машины способ численной оценки позиций, возникающих на шашечной доске. Если попросить человека сделать такую численную оценку, то он, возможно, сможет из шести разных позиций, представленных на рассмотрение, выбрать одну, наилучшую, и другую, самую худшую, но сказать что-нибудь вразумительное относительно четырех остальных ему будет гораздо труднее. А такая оценка недостаточно точна для того, чтобы ею могла воспользоваться вычислительная машина. Человек просто не прибегает, во всяком случае сознательно, к численным оценкам, нужным машине, и поэтому, как бы мы ни допрашивали гроссмейстеров, таких чисел нам не получить. (Впрочем, использование методов многомерного шкалирования может, вероятно, дать некоторое представление об этом.) Поэтому мы станем решать эту задачу с позиций теории адаптивного управления. Хотя мы и не имеем представления о том, с помощью какой функции оценивать возникающую на доске позицию, нам по крайней мере известно, что искомая оценка зависит от таких параметров, как число шашек у каждого игрока, число дамок, равновесие на доске, подвижность позиции каждого, контроль за центром и т. п. И дать каждому из этих параметров численную оценку не представляет особого труда. Выберем в результате бесед с игроками в шашки 16 таких параметров, играющих центральную роль в оценке позиции на доске.

На рис. 49 дано наглядное представление для двумерного случая. Здесь каждой паре значений параметров соответствует точка (x₁, x₂) на горизонтальной плоскости, а соответствующая оценка изображается точкой, лежащей от нее на расстоянии z=f(x₁,x₂) по вертикали. Если точка (x₁, x₂) перемещается по плоскости, то z=f(x₁,x₂) описывает некоторую поверхность, которую мы назовем оценочной поверхностью. На этой поверхности немало неровностей, но тем не менее она не так уж сильно отличается от некоторой плоскости, которую мы будем называть оценочной плоскостью. Из математики известно, что всякая плоскость описывается уравнением вида z=w₁x₁+w₂x₂-θ, где w₁, w₂ и θ должны иметь подходящие значения. Аналогично, какой бы "ухабистой" ни была оценочная "поверхность" в 17-мерном пространстве^*, которая каждой комбинации значений оценочных параметров ставит в соответствие глобальную оценку позиции на доске, мы все же можем надеяться, что для нее существует хорошая аппроксимация в виде плоскости и что эта аппроксимация позволит машине играть достаточно хорошо. Другими словами, мы можем надеяться найти хорошую оценочную функцию вида z=w₁x₁+w₂x₂+ ... +w₁₆x₁₆-θ (называемую линейным приближением) при подходящем выборе 16 весов w₁, ..., w₁₆ и θ. На самом деле для сравнения двух позиций постоянная θ несущественна, поскольку она добавляет ко всем оценкам одинаковую величину, но не меняет их разности, и, значит, нам нужно найти лишь 16 чисел, чтобы получить наилучшее линейное приближение.

^* (Координатами этого пространства являются 16 выбранных оценочных параметров и значение оценочной функции. - Прим, перев.)

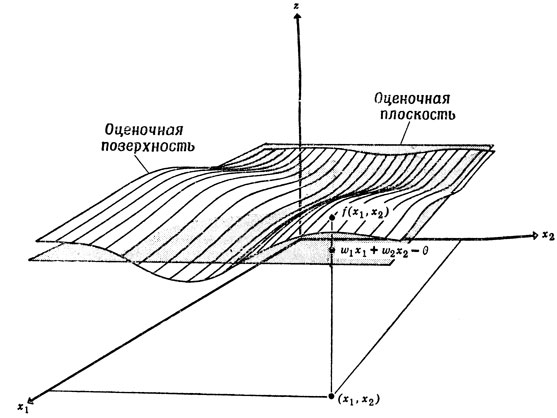
Рис. 49. Здесь показано, как с помощью плоскости (линейной поверхности) можно аппроксимировать нелинейную поверхность. Для каждой пары параметров (x₁, x₂) истинная оценка f(x₁, x₂) приближается линейной комбинацией w₁x₁+w₂x₂-θ

Таким образом, с позиций теории систем стратегия, принятая Сэмюэлом [221] в его первой статье, состояла в том, чтобы не только произвольно обрывать просчет позиции, но и предположить, что функцию оценки можно аппроксимировать линейной. Последнее было не более чем догадкой, которая могла оказаться совершенно бесполезной, но он положился на это допущение и стал исходить из того, что плоскость даст достаточно хорошее приближение 16-мерной оценочной поверхности и что, следовательно, единственное, что ему остается сделать, это определить 16 весовых коэффициентов, от которых зависит ориентация оценочной плоскости в 17-мерном пространстве.

Пусть в машине имеются текущие значения весовых коэффициентов линейной оценочной функции и она выбирает ход, который, по ее мнению, ведет к позиции с довольно высокой оценкой. Если через несколько ходов после этого выяснится, что игра развивается неудачно и что выбранная стратегия была, по-видимому, переоценена, машина уменьшает значения весовых коэффициентов при тех оценочных параметрах, которые свидетельствовали в пользу выбранного плана игры, и увеличивает их значения при параметрах, которые свидетельствовали против него. Конечно, на самом деле все гораздо сложнее, но существенно лишь то, что Сэмюэлу удалось написать программу, позволявшую вычислительной машине сравнивать свой прогноз с тем, что получалось на доске через несколько ходов в действительности, и соответственно регулировать коэффициенты оценочной функции. Первая шашечная программа Сэмюэла играла не слишком сильно, и это свидетельствовало о том, что линейная оценочная функция не так уж хорошо приближает "реальную". Позднее Сэмюэл [222] воспользовался значительно более сложной оценочной функцией, которую он назвал "таблицей сигнатур"; кроме того, он заложил в программу довольно богатую библиотеку из образцов лучших шашечных партий, сыгранных человеком, и все это вместе позволило программе достигнуть уровня мастера.

Итак, мы познакомились с задачей, в которой качество работы вычислительной машины можно значительно повысить, если вначале предложить ей целый класс возможных стратегий решения, а затем с помощью процедуры идентификации корректировать значения относительно небольшого числа параметров, заставляя машину адаптироваться к конкретным потребностям текущей ситуации. Аналогичные схемы адаптации используются, по-видимому, и в обучении человека после того, как найдена соответствующая структура в центральной нервной системе, в которой может осуществляться необходимая коррекция. Например, обучаясь водить автомашину, мы слышим вначале от инструктора слота, в определенном смысле аналогичные той программе, которую вводил Сэмюэл в свой шашечный автомат. (В других ситуациях такой готовой схемы, требующей лишь уточнения параметров, нет, и именно в этом случае мы начинаем говорить о творчестве.) Запомнив эту "программу", человек не начинает сразу же прекрасно управлять автомобилем, ему нужно еще скорректировать массу параметров. Ведь увидав помеху справа, мало просто повернуть налево, необходимо еще почувствовать, насколько именно нужно повернуть руль.

Сказанного выше достаточно, чтобы понять, что многие из взаимодействий мозга с окружающей средой могут быть квалифицированы как процедуры идентификации. И чтобы лучше разобраться в некоторых тонкостях подобных процессов, обратимся к следующему примеру.

Представьте себе, что вам нужно приподнять на 15 сантиметров куб, лежащий на столе. Если по внешнему виду кажется, что куб полый и сделан из стали (рис. 50), то можно предположить, что он достаточно легкий и его можно поднять одной рукой. Однако, если на самом деле дно куба, закрытое от вас передней стенкой, залито свинцом, он может оказаться слишком тяжелым и попытка поднять его одной рукой не увенчается успехом. Эта неудача заставит вас в корне изменить свои представления о весе куба и изменить свою стратегию, т. е. поднимать куб двумя руками. И наоборот, если, несмотря на свой обманчивый вид, куб состоит из легкого проволочного каркаса, обтянутого тонкой алюминиевой фольгой, сила, с которой вы потянете его вверх, окажется чрезмерной и вы рванете куб гораздо выше, чем намеревались, так что потом придется опускать его до выбранного уровня. Таким образом, в дополнение к различным механизмам обратной связи (разд. 5.2), позволяющим плавно корректировать незначительные промахи двигательной системы, должны существовать и механизмы более высокого уровня, отвечающие за то, чтобы мы вообще "не ошиблись адресом", и только это позволит успешно взаимодействовать со средой. Кассетная метафора, с которой мы познакомимся в разд. 4.1, даст некоторые представления о том, как это можно делать (см. также разд. 5.5). Пример с подниманием куба (рис. 50) привлекает внимание к нескольким важным вопросам.

Рис. 50. Полый ли этот стальной куб

1. Необходимо понять, что имеющийся объект - это ящик, и из многих возможных взаимодействий с ящиком выбрать то, которое требует его поднимать.

2. Организм должен решить, какое поведение эффекторов обеспечит необходимое воздействие на ящик, в результате которого будет достигнута поставленная цель.

3. Мозг должен вычислить необходимые сигналы и послать их в спинной мозг, с тем чтобы мотонейроны могли реализовать сокращение необходимого набора мышечных волокон, обеспечивающее требуемое поведение эффекторов.

К такой декомпозиции на три стадии нужно отнестись с определенной осторожностью по причинам, о которых пойдет речь ниже.

I. Эти три стадии могут, по крайней мере частично, выполняться одновременно. Как мы узнаем из разд. 7.2, в мозгу лягушки, по-видимому, "запаяны" такие структуры, что она вообще не нуждается в стадиях 1 и 2. У нас нет оснований считать, что лягушка сначала распознает муху, затем решает схватить ее, затем выбирает подходящую траекторию для языка и, наконец, вычисляет последовательность нейронных команд, реализующих схватывание мухи. Нам кажется, что лягушка вообще не может распознать муху (или "дрожащий" объект), если она не произведет соответствующей ориентации или не нападет на нее. [Здесь нужно сделать два предостережения: а) передний мозг может изменить поведение лягушки: она не станет раз за разом нападать на шмелей; б) приходится признать, что парализованная лягушка, распознает муху, поскольку нейроны, которые в норме управляют реакцией нападения, приходят у нее в возбужденное состояние. В общем тезис состоит в том, что восприятие объекта (по крайней мере на довербальном уровне) состоит в получении доступа к программам взаимодействия с ним, а не в обязательном осуществлении хотя бы одной из таких программ. Мы еще вернемся подробнее к этому тезису в разд. 6.1.]

II. Заметим, что даже тогда, когда человек ясно сознает, какой именно объект находится перед ним и что он собирается с ним делать, осознанная оценка (т. е. оценка, которую можно выразить словами) параметров объекта вроде его веса совсем не обязательна. Вполне достаточно, чтобы распознавание и принятое решение приводили к такому выбору путей от рецепторов к эффекторам, который обеспечит действие эффекторов в соответствии с имеющимися значениями существенных параметров. Эту мысль можно развить, задав себе вопрос, а что случилось бы, если бы мы сообщили Сэмюэлу 16 чисел w₁, w₂, ... , w₁₆, используемых его программой. По-видимому, сам Сэмюэл не стал бы от этого лучше играть в шашки. Обычно отсюда приходят к выводу, что эти числа не имеют ничего общего с тем, как играет сам Сэмюэл, и что, следовательно, весь этот поиск по дереву решений, все эти численные оценки и коррекция весовых коэффициентов не имеют ничего общего с тем, как играют люди. Именно поэтому знание весовых коэффициентов не поможет Сэмюэлу. Однако рассмотрим один не вполне обычный довод, который, хотя я и не думаю, чтобы он оказался верным в данном конкретном случае, позволяет несколько лучше понять, с чем нам приходится сталкиваться при моделировании работы мозга. Представьте себе, что ваш мозг работает как нейронная сеть, которая, получив информацию о позиции на доске, не рассматривает шаг за шагом сначала последствия одного хода, затем другого и т. д., а вместо этого, "ухватив" всю позицию как нечто целое и "записав" ее в несколько нейронных структур, одновременно вносит в каждый из полученных образов какие-то разные возмущения, а затем организует взаимодействие задействованных структур, и так до тех пор, пока не придет к конечному результату без какой-либо помощи со стороны централизованного управления. Предположим теперь (но я подчеркиваю, что это делается лишь в качестве аргумента в споре, а на самом деле в мозгу нет такого простого соответствия), что в таком мозгу существуют 16 регулируемых синапсов, роль которых в точности соответствует роли 16 весовых коэффициентов в программе Сэмюэла! В таком случае, даже если сообщить Сэмюэлу точные значения весов соответствующих синапсов, он не сможет воспользоваться этим явным знанием для того, чтобы отрегулировать значения этих весов, и самое лучшее, что ему останется, - это по-прежнему регулировать их, играя партию за партией. (Независимо от ценности приведенной аргументации она лишний раз напоминает нам о том, что современные машины работают почти исключительно в последовательном режиме, а мозг функционирует почти исключительно в параллельном.)

III. Однако люди иногда пользуются для обработки информации алгоритмами более высокого уровня и воздерживаются от действий, прежде чем не проанализируют незнакомый предмет, который нужно поднять. Например, человек скажет себе: "Гм, это похоже на два стула, связанных вместе, и, значит, весит примерно как стол", и только после этого начнет возбуждать в выходных нейронных структурах активность, подобную той, которая потребовалась бы для того, чтобы поднять соответствующим образом стоящий стол. Эта способность использовать "декомпозицию" и "построение аналогий" для оценки системы, избавляющая от необходимости прибегать к физическим экспериментам с ней, является очень важной чертой человеческого поведения. Предвесники такой способности можно найти и у животных, и, как нам кажется, именно на этой основе возник язык.

IV. В наших рассуждениях важную роль играют соображения "деенаправленности". Если вы решили поднять стул, то детали его конструкции и материал обивки несущественны, а его вес-важнейший параметр. И, напротив, если вы собираетесь нарисовать этот стул, то его вес не будет иметь никакого значения, а первые два признака станут весьма существенными. Мы стараемся обращать внимание только на те свойства объекта которые важнее всего с точки зрения немедленного или будущего взаимодействия с ним. В сущности часто мы даже не воспринимаем объект как таковой, а лишь отмечаем его отдельные черты. Так, на стадии 1 описанного выше процесса мы можем вовсе не воспринимать ящик как таковой, а лишь решить, что его нужно поднять, например для того чтобы подстелить под него скатерть.

Итак, для того чтобы система могла успешно взаимодействовать со сложной средой, ей необходима широкая "информационная база" или "внутренняя модель мира", но полезность даже относительно простой модели мира можно во много раз увеличить, если предусмотреть возможность коррекции параметров, осуществляющих адаптацию модели к новым или изменившимся обстоятельствам.