В лабиринте слов

Человек склонен глубоко проникать во все явления и искать законы, по которым они протекают. Для этого ему часто приходится, как говорил Ломоносов, "сближать далековатые идеи".

Что, казалось бы, может быть общего между словами и числами? Но человек сумел числа подчинить законам слов, а слова - законам чисел.

Помните веселую историю, рассказанную Джеромом К. Джеромом в книге "Трое в одной лодке, не считая собаки"? Сколько людей смеялось над чудаком Гаррисом, попавшим в Хемптонкортский лабиринт!

- Мы только зайдем сюда, чтобы ты мог сказать, что побывал в лабиринте, но это совсем не сложно. Даже нелепо называть его лабиринтом. Мы походим здесь минут десять, а потом отправимся завтракать, - уговаривал Гаррис своего родственника.

Но увы! Он не только заблудился сам, но и запутал людей, которых взялся избавить от мучительного блуждания по лабиринту. За ним следовало по крайней мере человек двадцать и даже одна женщина с ребенком, безуспешно искавшая выход из лабиринта все утро.

Следуя своей тактике, Гаррис все время поворачивал направо. Ему казалось, что вот-вот он выберется из лабиринта. Но время шло, и... вся компания во главе с Гаррисом вернулась к тому месту, где они уже были. Половинка булочки, брошенная ребенком и замеченная родственником Гарриса семь минут тому назад, с несомненностью указывала место их недавнего пребывания.

Тогда Гаррис предложил вернуться назад и начать все снова. Предложение начать снова особого энтузиазма не вызвало, но все согласились вернуться.

Процессия повернула обратно и потянулась за Гаррисом в противоположном направлении, но через десять минут вся компания снова очутилась в центре лабиринта. Такой же неудачей закончились и последующие попытки. В какую бы сторону они ни сворачивали, все пути приводили их в центр. Это стало повторяться с такой правильностью, что некоторые просто оставались на месте и ждали, пока остальные прогуляются и вернутся к ним. Наконец отчаявшиеся любители лабиринта призвали на помощь сторожа, который и вывел их на "свободу".

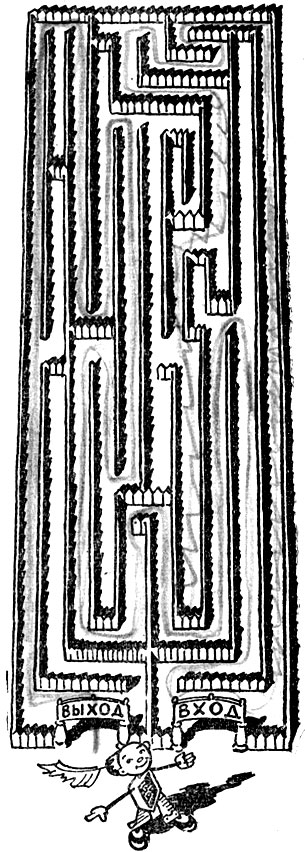
Попробуйте пройти этот лабиринт!

Бедному Гаррису не пришлось бы блуждать и мучить людей, если бы он знал, как решается лабиринтная задача. Она является математической задачей особого вида, для решения которой существует алгоритм.

Лучше всего ее изложить на примере простого лабиринта. Вот перед нами его план. Войдем в лабиринт. Площадку у входа обозначим буквой Л. Остальные площадки, соединенные коридорами, обозначим другими буквами алфавита.

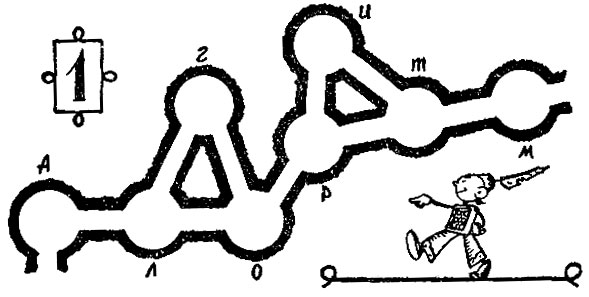
План простого лабирин

Теперь начнем искать выход из лабиринта. Следуя "методу" Гарриса, повернем направо и прогуляемся до площадки Л. От нее расходятся два коридора. Один ведет прямо, другой налево. Какой же из них выбрать?

Будем действовать так, как, наверное, рассуждал бы Гаррис. Если направо поворачивать некуда - свернем налево. Такой путь приведет нас на площадку Г.

Теперь путь направо открыт. Поворот направо - коридор, и мы на площадке О. Опять поворот направо, и... мы вновь очутились на площадке Л. Здесь родственник Гарриса мог бы обнаружить булочку, брошенную ребенком.

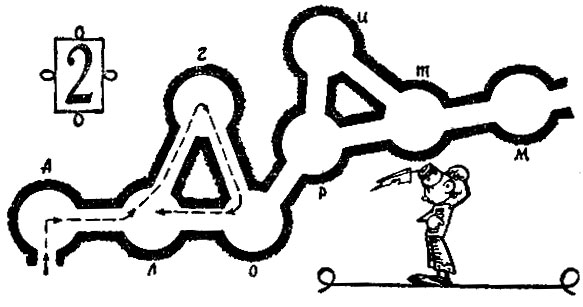
Повороты направо приведут к постоянному возвращению на площадку 'Л'

Теперь повороты направо приведут к постоянному возвращению на площадку Л. Такой "алгоритм" и привел Гарриса к неудаче. К тем же результатам приведет постоянный поворот налево.

Как же быть? Какое руководство к действию обеспечит выход из лабиринта (если, конечно, он существует) любому человеку, даже Попавшему в него впервые в жизни?

Для тoгo чтобы усвоить этот алгоритм, обозначим коридор, пройденный один раз, пунктирной линией, а коридор, пройденный дважды, - сплошной линией. Будем руководствоваться в наших поисках такими указаниями:

Первое. Если от площадки идет хотя бы один коридор без отметки - иди по нему. Если таких коридороЁ несколько, выбирай сначала правый, потом левый, потом прямо. Пройдя коридор в первый раз, отметь его пунктиром.

Второе. Если пунктирная линия замкнулась - иди по ней назад до первой же площадки, имеющей коридоры без отметки. Вместо пунктирной линии проводи сплошную. Коридоры со сплошной линией считай закрытыми., В них входа нет.

Конечно, вместо пунктирной и сплошной линий в лабиринте можно было бы ставить у входов в коридоры другие отметки. Гаррис, у которого ничего не было, мог бы для этой цели использовать кусочки булочки. Один кусочек класть у входа в коридоры, где он побывал один раз, и два кусочка возле коридора, где он побывал дважды.

Теперь начнем искать выход из лабиринта. Пойдем вначале так, как мы это делали в первый раз. НаЩ путь на плане отмечен пунктирной линией.

Вернувшись на площадку Л, будем действовать по указанию второму. Идем назад до площадки О, а коридор ЛО отмечаем сплошной линией.

От площадки О идет только один свободный (без отметки) коридор. Идем по нему до площадки Р, затем по указанию первому на площадку Т. Здесь коридора направо нет, идем налево до площадки И, а от нее вновь возвращаемся на площадку Р.

Не будем падать духом, а беспрекословно выполним второе указание руководства к действию. Раз пунктирная линия замкнулась, возвращаемся назад до площадки Т, & коридоры РИ и ИТ отмечаем сплошной линией. На Площадке Т есть коридор без отметки. Он ведет к площадке М - к выходу из лабиринта.

Если бы нас заставили второй раз пройти через лабиринт, то по пунктирным линиям АЛ, ЛГ, ГО, ОР, РТ, ТМ мы быстро и безошибочно нашли бы правильный путь.

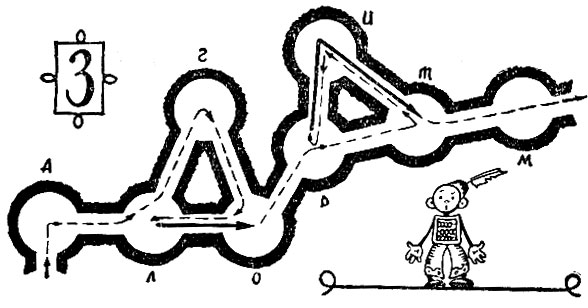
Выход из лабиринта найден

Наше путешествие по лабиринту оказалось все-таки достаточно долгим и утомительным. Если не связывать себя жестким правилом о порядке выбора свободного 'коридора, то, возможно, путешествие закончилось бы намного раньше.

В самом деле, представим себе, что, придя с площадки Р на площадку Т, мы не повернули бы налево, а вместо этого бросили бы жребий - монету. Герб - идти налево, решка-прямо. При выпадении решки мы двинулись бы по коридору ТМ и без излишних блужданий покинули бы лабиринт.

Руководство к действию можно построить и на случайном выборе свободного коридора. При "везении" это сократило бы поиски выхода.

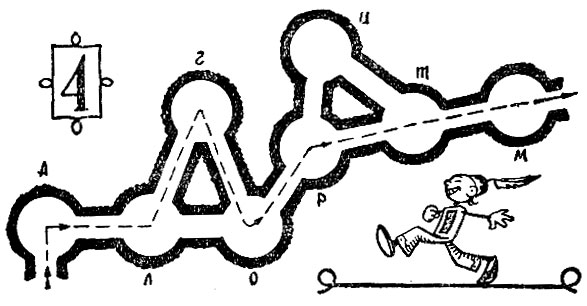
Теперь путь от входа к выходу ясен

Лабиринтная задача дает ответ на один из вопросов, волнующих многих ученых, - можно ли найти алгоритмы для решения не только математических задач, но и других, связанных с умственной деятельностью человека.

Какая заманчивая идея заложена в этом и какие огромные возможности сулит ее претворение в жизнь! Ведь это означает, что всюду, куда проникнет алгоритм, умственный труд человека рано или поздно может быть заменен машиной. Мозг человека будет освобожден от однообразного и утомительного повторения указаний "руководства к действию".

В семидесятых годах прошлого столетия появилась 'Игра в 15'

Поэтому тысячи ученых упорно трудятся над изучением различных задач и проблем, чтобы построить для них алгоритмы и создать машины для автоматического выполнения "руководства к действию"...

Кое-что уже удалось сделать. Разработаны алгоритмы, по которым удобно автоматизируются решения большинства математических задач, создаются алгоритмы перевода текстов с одного языка на другой, алгоритмы решения ряда задач по управлению производством и даже алгоритмы различных игр.

В семидесятых годах прошлого столетия в Америке появилась "Игра в 15". И в наше время многие знакомы с квадратной коробочкой, внутри которой помещены 15 шашек, пронумерованных цифрами от 1 до 15. Одна клеточка в коробке свободна. Игра заключается в следующем: все пятнадцать шашек сначала располагаются в произвольном порядке. Передвигая (но не вынимая) шашки, нужно расположить их в порядке возрастания номеров.

Немецкий математик Арене, занимавшийся исследованием игр, рассказывает, что "Игра в 15" распространилась с неслыханной быстротой по всей стране и превратилась в настоящее общественное бедствие. Игра очень быстро проникла и в другие страны Европы и завоевала множество усердных любителей. Хозяева контор и магазинов приходили в отчаяние от увлечения своих служащих и вынуждены были запретить им игру в часы занятий и торговли. Даже в торжественных залах германского рейхстага игра нашла горячих поклонников. "Как сейчас вижу в рейхстаге седовласых людей, сосредоточенно рассматривающих в своих руках квадратную коробочку", - вспоминает известный географ и математик Гюнтер, бывший депутат в годы игорной эпидемии.

'Игра в 15' распространилась с неслыханной быстротой и превратилась в настоящее общественное бедствие

В Париже "Игра в 15" нашла приют под открытым небом на бульварах и быстро распространилась из столицы по всей провинции. "Не было такого уединенного сельского домика, где не гнездился бы этот паук, подстерегая жертву, готовую запутаться в его сетях", - писал один французский автор.

Содержатели увеселительных заведений ловко использовали эту манию и устраивали большие игорные турниры. За решение нескольких задач назначались огромные премии.

Сам изобретатель игры Самуэль Ллойд предложил издателю нью-йоркской газеты опубликовать одну из таких задач с премией в тысячу долларов за ее правильное решение. Премию никому завоевать не удалось, хотя все без устали пытались найти простое на первый взгляд решение задачи.

'Игра в 15' распространилась с неслыханной быстротой и превратилась в настоящее общественное бедствие

Рассказывали забавные истории о торговцах, забывавших открывать свои магазины, о почтенных чиновниках, целые ночи напролет простаивавших под уличным фонарем, отыскивая путь к решению. Штурманы из-за игры сажали на мель свои суда, машинисты без остановок проводили поезда мимо станций. Фермеры забрасывали свои плуги. Никто не желал отказаться от поисков решения, так как чувствовал уверенность в ожидаемом успехе.

Игорная горячка и погоня за премией вскоре прекратились; неразрешимость ряда задач, и в том числе премиальной, была доказана математиками. Они сумели ответить на вопросы: всегда ли возможно перевести шашки из любого начального положения в порядок возрастающих номеров? А если нет, то существует ли короткий алгоритм, позволяющий' сразу определить, разрешима задача или нет? Или это можно обнаружить, только перепробовав все комбинации?

'Игра в 15' распространилась с неслыханной быстротой и превратилась в настоящее общественное бедствие

Заметим прежде всего, что самый простой на первый взгляд алгоритм - это перебор всех возможных позиций, которые получаются из заданной, если передвигать шашки, соблюдая правила игры. И если среди этих позиций оказывается та, в которую шашки нужно перевести, то задача разрешима, а если нет - неразрешима.

Но при таком способе может возникнуть необходимость перебора до двадцати триллионов позиций! Если на передвижение шашек из одной позиции в другую затрачивать только десятую долю секунды, то для этого потребовались бы тысячи лет непрерывной работы! Согласитесь, что такой алгоритм нельзя признать удачным.

Если бы математики не нашли более короткий путь обнаружения неразрешимых задач, то еще много-много лет продолжалась бы бессмысленная погоня за премией. Пока не были бы перепробованы все комбинации, ее искатели не успокоились бы.

'Игра в 15' распространилась с неслыханной быстротой и превратилась в настоящее общественное бедствие

Быстрый способ обнаружения неразрешимой задачи несложен. На рисунке на следующей странице показано заданное в начале игры расположение шашек. Теперь попробуйте, вынимая шашки из коробки, менять их местами до тех пор, пока они расположатся по возрастающим номерам. Если таких перестановок окажется четное число, то задачу можно решить и путем передвижения шашек. Если же число перестановок нечетно - задача неразрешима. В нашем случае перестановок четное число - задача разрешима!

В задаче, за решение которой была обещана премия в тысячу долларов, все шашки, кроме двух последних, располагались в порядке возрастания номеров. Но шашки 14 и 15 стояли в обратном порядке: сначала 15, а за ней 14. Нужно было передвижением любых шашек поменять их местами. Но мы уже знаем, это сделать невозможно. Порядок в расположении шашек достигается одной перестановкой - нечетным числом. Такие задачи передвижкой шашек неразрешимы.

Неразрешимый и разрешимый случай

Любеке беспорядочное расположение шашек в "Игре в 15" можно передвижением привести либо в нормальный порядок либо к позиции, в которой шашки 14 и 15 меняются местами. В первом случае мы имеем дело с разрешимыми задачами, во втором - с неразрешимыми.

Теперь для "Игры в 15" не нужно искать остроумных решений. Исход игры не зависит от каких-либо случайных обстоятельств или от находчивости игрока. Он точно предопределен алгоритмом, и по нему машина может играть с таким же успехом, как и человек.

Как ни покажется странным, но между "Игрой в 15" и лабиринтом есть большое сходство. Чтобы в этом убедиться, попробуйте решить такую своеобразную задачу.

Вот несколько имен: Геня, Таня, Соня, Ваня, Маня, Сеня, Саня, Вася. Составьте из них цепочку, по которой можно было бы переделать имя Геня в имя Вася, меняя каждый раз в имени только одну букву.

От Гени к Васе

Перебирая всевозможные комбинации, мы без труда построим необходимую цепочку. Она перед нами:

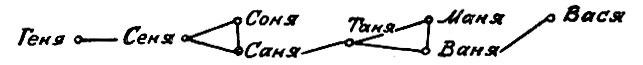
Сравните ее с лабиринтом, и вам сразу станет ясным сходство задачи поиска пути в лабиринте с задачей преобразования имен.

Имена-площадки в лабиринте, а допустимый порядок изменения букв - коридоры. Они соединяют в лабиринте площадки, а в цепочке имен - смежные имена, отличающиеся друг от друга одной буквой.

При решении задачи с именами можно тоже пользоваться алгоритмом поиска пути в лабиринте. Но в нашем случае для перехода от "Гени" к "Васе" можно обойтись без этого. Имен не так много, и простой подбор быстро дает результат.

Можно придумать много других подобных игр в слова. Попробуйте, например, сделать из "мухи" "слона". Это легко удается людям, склонным к преувеличениям. При этом нужно обладать, мягко говоря, очень большой фантазией. Но предложите им переделать слово "муха" в слово "слон", соблюдая определенные правила, ограничивающие фантазию. Тогда они поймут разницу между этими словами.

Вот правила. Менять можно каждый раз только одну букву. Но при этом каждое полученное слово должно иметь смысл. Легко, например, получить слово "слон" из слова "стук" по таким переходам:

"Стук - сток - стон - слон".

Чтобы перейти от "мухи" к "слону", нужно тоже построить цепочку промежуточных слов. Это делается только путем подбора-более короткого алгоритма нет. Надо выписать все существующие в русском языке слова из четырех букв и, пробуя всевозможные комбинации, подобрать необходимые слова или убедиться в том, что такой цепочки не существует. Но возможные комбинации выражаются большим числом - 810 тысяч. Пришлось бы немало потрудиться, чтобы построить одну из возможных цепочек перехода слов. Ведь это значит, что надо искать выход в лабиринте не с восемью площадками, а со многими сотнями площадок и тысячами коридоров. Например, от площадки "муха" ведут коридоры к словам "мука", "мура", "меха" и ко многим другим смежным словам, отличающимся от "мухи" одной буквой. И так на каждой площадке.

Как сделать из 'мухи' 'слона'

По нашей просьбе профессор математики Э. Кольман решил эту задачу. Он взял орфографический словарь на ПО тысяч слов и среди 1 865 четырехбуквенных слов выбрал 75 с двумя гласными в середине. Только с их помощью можно осуществить переход.

Остроумно комбинируя слова, Э. Кольман сделал из "мухи" "слона". Попробуйте это сделать сами.

Из "Игры в 15" можно тоже сделать "Игру в слова". Напишите на шашках вместо цифр буквы и расставьте их так, чтобы образовались следующие слова: "февраль, "быт", "жди", "ус". Как видите, пятнадцать букв - и все разные. Попробуйте передвижением шашек полу* чить из них слова "фестиваль дружбы". В них тоже пятнадцать букв.

Эта игра со словами похожа на предыдущую и тоже является разновидностью лабиринтной задачи. И здесь различные позиции площадки лабиринта, а допустимый порядок замены букв, ходы,- коридоры. В таком лабиринте неизмеримо больше площадок и коридоров, чем в лабиринте "муха" - "слон", и получить ответ простым перебором невозможно.

Но с помощью известного нам алгоритма легко проверить, разрешима ли эта задача. Потребуется нечетное число перестановок шашек с буквами, а именно одиннадцать. Значит, передвижкой шашек преобразовать одну комбинацию слов в другую невозможно.

Игры в слова могут показаться пустой забавой. Но на самом деле за ними кроется очень глубокий научный смысл. Мы уже рассказывали, что математики стремятся находить алгоритмы для решения все более и более общих математических задач. После того как удалось найти формулы для вычисления корней кубического уравнения, стали искать формулы для корней уравнения четвертой степени.

Когда и эти формулы были найдены, ученые много десятилетий пытались сделать то же самое для уравнений пятой и более высокой степени. Эти попытки оказались безуспешными, а в начале XIX века удалось доказать, что таких формул не существует. Но тогда нашли другие методы решения любых уравнений высоких степеней, менее удобные, чем вычисления корней по формулам, но зато и более общие. То же самое происходит и в иных областях математики.

А нельзя ли построить алгоритм, позволяющий решать любую математическую задачу? Вот вопрос, который несколько столетий привлекал внимание самых выдающихся математиков.

Еще великий немецкий математик и философ Лейбниц мечтал о создании всеобщего метода, позволяющего доказать любую теорему, решать любую задачу. Сделать это ему не удалось. Но великий ученый был уверен: наступит время, и такой "всемогущий" алгоритм будет найден.

Величественное здание математики покоится на системах аксиом. Так, мы уже знаем, что на аксиомах Эвклида строится вся классическая геометрия. Из наблюдений над явлениями природы, из обобщений многовекового опыта человечества формулируются аксиомы - предложения, применяемые без доказательств. Они образуют тот фундамент, на котором по строго доказанным правилам строится математическая теория.

От аксиом ко всем теоремам данной теории ведет длинный путь доказательств, подчиненный точным законам формальной логики.

Но мы уже знаем, что каждую аксиому можно по законам математической логики записать в виде формул. А каждая такая формула - это слово, составленное из букв, скобок, символов, вроде И, ИЛИ, НЕ и так далее. Точно так же каждая теорема - это слово с другой комбинацией букв, скобок и прочих символов.

Значит, путь от аксиом к теоремам-это путь в лабиринте слов, в котором буквы и символы можно менять по вполне определенным правилам. Так, например, слова "не неправильный" можно заменить словом "правильный", вместо "прямая АВ или прямая АВ" можно написать просто "прямая АВ".

Но существует этот путь или нет? Именно на этот вопрос и должен давать ответ "всемогущий" алгоритм.

Теперь нетрудно понять, насколько заманчиво иметь такой алгоритм. Ведь тогда можно было бы почти наугад сформулировать любую теорему и с его помощью проверить, имеется ли путь в лабиринте слов от аксиом к этой теореме, подобно тому, как мы проверяли лабиринт в "Игре в 15". При положительном ответе алгоритм указал бы и кратчайшую дорогу, а отрицательный ответ означал бы: "пути не существует, и не следует терять силы на попытки доказать недоказуемое".

"Всемогущий" алгоритм в руках математика явился бы мощным единым средством для решения всех сформулированных, но еще до сих пор не решенных математических задач. Более того, претворив такой алгоритм в машинное руководство к действию, можно было бы создать "гениальный" математический автомат.

Поэтому многие ученые во всем мире упорно занимались поисками "всеобщего" алгоритма. Но тщетно! Все попытки оказались безуспешными, столь же безуспешными, как попытки средневековых алхимиков найти философский камень, превращающий любой металл в золото, или составить "жизненный эликсир", дарующий бессмертие.

Возникло сомнение в самом существовании всеобщего алгоритма. Но это были лишь сомнения. Строго доказать невозможность построения его оказалось делом не менее трудным, чем найти.

Вспомните, что до сих пор никому не удалось решить десятую проблему Гильберта - найти или, наоборот, доказать невозможность построения алгоритма для решения Диофан-товых уравнений.

И вот совсем недавно математический мир узнал о выдающемся достижении советской математической науки. Член-корреспондент Академии наук СССР П. С. Новиков доказал алгоритмическую неразрешимость одной из задач преобразования слов. Ему удалось найти пример преобразования слов в одной из современных областей математики - теории групп, для которого строго доказана невозможность построения алгоритма.

Работа Новикова, за которую он удостоен Ленинской премии, имеет огромное значение. Она показала, что процесс познания в математике не может быть втиснут в рамки алгоритма. Создать "гениальный" математический автомат невозможно.,