Подведем итог

Перед нами старинный том. На переплете тиснение золотом "Решения и постановления Парижской Академии наук за 1775 год". Открываем книгу и читаем: "Академия постановила: отныне и впредь не рассматривать представляемых ей разрешений задач трисекции угла, квадратуры круга, удвоения куба, а также машин, долженствующих осуществить вечное движение".

Что за странное постановление? Пожалуй, можно согласиться, что в отношении вечных двигателей оно разумно. Видно, нужно было как-то избавить ученых от докучливых изобретателей, осаждавших Академию наук своими прожектами.

'...Отныне и впредь не рассматривать... разрешений задач трисекции уела, квадратуры круга, удвоения куба...'

Но зачем понадобились специальные постановления высокоавторитетного научного учреждения по поводу задач, решение которых не составляет труда для любого школьника?

Не делайте, однако, поспешных выводов. Парижская Академия наук имела в виду не совсем обычные математические "изобретения".

Три математические задачи, которые упоминаются в постановлении, были сформулированы еще в древности греческими геометрами. Мы уже рассказывали, что они презрительно относились ко всякого рода вычислениям. Подлинно научными считались только чисто геометрические методы. Решение задачи признавалось лишь в случае, когда оно достигалось только с помощью циркуля и линейки без делений.

И вот три задачи так не решались. Не получалось деление произвольного угла на три равные части, не могли найти сторону квадрата, площадь которого равна площади круга заданного радиуса. Не могли найти сторону куба, объем которого вдвое больше объема заданного куба.

Многие столетия люди пытались найти алгоритм для решения этих задач циркулем и линейкой. Но все попытки окончились неудачей. Три древние задачи снискали печальную известность неразрешимых.

Из них одна стала знаменитой и даже вошла в поговорку. "Квадратура круга!" - так часто говорят, когда хотят подчеркнуть безвыходность положения или указать на очень трудную задачу. Писатели этими словами озаглавили не одно произведение,например О' Генри - известный рассказ, а Валентин Катаев - пьесу.

Еще в древности сложилось мнение, будто квадратура круга при разгадке даст ключ ко многим тайнам природы и позволит сделать необыкновенные открытия. Одно время даже распространился слух, будто английский парламент и голландское правительство установили крупную премию за разрешение квадратуры круга.

Парижская Академия наук вынесла свое постановление, когда было строго доказано, что решение древних задач с помощью циркуля и линейки невозможно.

Но означает ли это, что вообще нет методов их решения, что они относятся к числу алгоритмически неразрешимых? Безусловно, нет!

Каждый решит подобные задачи без труда, но не циркулем и линейкой, а алгебраически или другим путем.

Это приводит, естественно, к такому вопросу: а как же обстоит дело с алгоритмически неразрешимой проблемой, открытой П. С. Новиковым? Мы только убедились, что возможность или невозможность построения алгоритма зависит от тех средств, которые используются для его реализации.

А раз так, то проблему преобразования слов, может быть, постигнет участь древнегреческих задач?

Квадратура круга

Современными средствами математики проблема преобразования слов оказалась действительно алгоритмически неразрешимой. Но математика все время идет вперед, а ее методы и средства постоянно совершенствуются. Можно ли при этом утверждать: никогда и никакими средствами построить алгоритмы для проблемы преобразования слов и других подобных задач не удастся? И никогда не удастся создать машину, способную полностью заменить математика?

Машина Тьюринга, Ее вид каждый может представить по-своему

Да, можно! И как это ни покажется странным, такая уверенность базируется на изучении возможностей вычислительной машины.

В 1936 году английский математик А. Тьюринг предложил самую простую и вместе с тем самую общую условную схему автоматической вычислительной машины. Она, по замыслу создателя, должна была работать как вычислитель, снабженный бумагой, карандашом и резинкой и не знающий даже правил сложения. Предполагается, что вычислитель может только точно и беспрекословно выполнять руководство к действию.

Сравнивая работу вычислителя с работой машины Тьюринга, нужно ввести еще одно условие. Снабдить вычислителя неограниченным количеством бумаги. Какими бы длинными ни были его вычисления - недостатка в бумаге для записи промежуточных результатов он испытывать не должен.

Машина Тьюринга вместо листов бумаги использует бесконечной длины бумажную ленту, которая приводится в движение электродвигателями, управляемыми специальным блоком.

Лента разделена на клетки. Клетка может быть пустой. Это означает, что в ней стоит О. В клетке может стоять также или I, или значок Δ, который отделяет одно число от другого.

В машине имеется приспособление - "глаз". Он обозревает одну клетку, расположенную в его "поле зрения".

Наконец машина снабжена приспособлением, с помощью которого она может вписывать в клетку один из двух значков или, наоборот, стереть то, что в клетке записано. Машина работает тактами, как, например, автомат, набивающий папиросы. Такт - папироса готова. Следующий такт - еще папироса.

В каждом из тактов машина Тьюринга может выполнить одну из следующих простейших операций: сдвинуть ленту на одну клетку вправо или влево или оставить ее на месте, стереть написанный в клетке значок или вписать в клетку I или Δ. Наконец машина способна остановиться, когда необходимо.

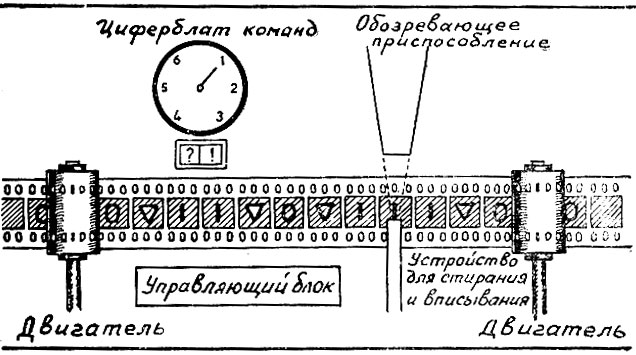
Схема машины Тьюринга

Все это происходит автоматически. Операциями руководит блок управления. В него встроен циферблат со стрелкой. Стрелка показывает номер команды-указание к действию. В зависимости от того, на какой команде стоит стрелка и что видит "глаз", машина производит перечисленные выше операции,

В конце такта стрелка, перескакивает на другую цифру. Машина переключается на выполнение следующего такта. Устройство, спрятанное за циферблатом, и "глаз" как бы командуют машиной. Они осуществляют руководство к действию.

Заставим машину автоматически сложить два числа. Например, 3 и 2. Их нужно написать на ленте. Первое число в виде трех единиц, второе - двумя единицами. Оба числа надо отделить друг от друга и от других пустых клеток на ленте значками Δ.

Складывать числа машина будет самым примитивным способом - по единицам.

Интересно проследить за работой машины, выполняющей сложение. Перед нами таблица руководства к действию, по которой работает блок управления машиной. В верхней строчке указано то, что машина может увидеть в клетке. А в левом столбце зарегистрированы все возможные положения стрелки циферблата блока управления, настроенного на сложение. В остальных клетках вписаны операции, которые в том или другом случае выполняются машиной. Это программа работы, реализуемая блоком управления. Так, например, если в клетке написана I, а стрелка циферблата стоит на цифре 4, то в этом такте двигатели сдвинут ленту на одну клетку вправо. Стрелка циферблата в конце такта перескочит на цифру 6.

В начале работы поставим стрелку на цифру 1. Ленту установим так, чтобы вторая единица числа 3 стояла против "глаза". Пустим машину в ход. Она начнет сложение: вычеркнет единицу из одного числа и прибавит ее ко второму. Затем вычеркнет еще одну единицу первого числа и снова прибавит ее ко второму.

Это будет продолжаться до тех пор, пока все единицы первого числа будут приписаны ко второму.

Вся "деятельность" машины строго регламентирована командами, написанными в таблице.

Проследите внимательно по ней за работой машины, и вы убедитесь, что ровно через 37 тактов сложение будет закончено. На ленте выстроятся подряд пять единиц, и машина остановится.

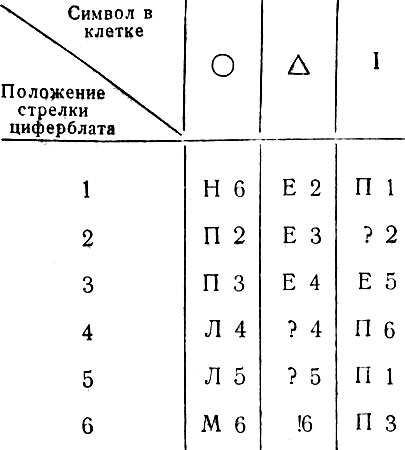
Таблица команд для сложения

Условные обозначения:

Л - продвинуть ленту на одну клетку влево.

П - продвинуть ленту на одну клетку вправо.

Н - написать в клетке I.

М - написать в клетке Δ.

Е - стереть знак в клетке (поставить Ο).

! - окончание вычисления.

? - что-то неверно - проверить!

Попробуйте сами составить таблицу команд для вычитания чисел. Это сделать не трудно. Машина должна по очереди зачеркивать единицы из уменьшаемого и вычитаемого.

Когда все единицы меньшего числа будут зачеркнуты, она должна остановиться. Единицы, оставшиеся от второго числа, дадут искомую разность.

Можно составить таблицы команд и для остальных арифметических действий: умножения и деления. По ним машина будет автоматически выполнять и эти операции.

Вообще машина Тьюринга может автоматически решить любую задачу. Необходима только таблица команд, то есть руководство к действию.

Но вот оно составлено, и тогда решение сложной задачи сводится к выполнению однообразных и самых простых операций - проще уже не выдумаешь! Так сказать, победа достигается не умением, - а числом!

В киножурналах и телевизионных передачах очень часто показывают работу различных сложных автоматов. Они завертывают конфеты, упаковывают мыло, набивают папиросы, шьют ботинки.

Наблюдая за их работой, нельзя не удивляться хитроумным движениям многих рычажков, заменяющих ловкие пальцы человека. Но самые замысловатые движения всегда образуются комбинированием только двух простейших: поступательного и вращательного.

Еще более удивительна работа машины Тьюринга. Комбинируя всего семь простых операций: сдвиг ленты вправо, влево, остановка ленты на месте, стирание символа, вписывание его, переход к следующей команде и остановка машины, - она может решать самые сложные математические задачи, переводить тексты с одного языка на другой, играть в домино, шашки, шахматы, искать выход из лабиринта.

Тьюринг доказал, что любой вычислительный или логический процесс, для которого существует алгоритм, может быть автоматизирован с помощью этой примитивной машины.

Он показал и обратное: все, что можно сделать с помощью его машины, подчинено алгоритму. А задачи, которые этой машиной не решаются - алгоритмически неразрешимы. Для них алгоритм никогда не будет найден.

К таким именно задачам и относится задача преобразования слов в теории групп. Новиков доказал, что машина Тьюринга эту задачу решить не может. Здесь она бессильна.

В этом бессилии машины Тьюринга заключается огромный смысл: результат Новикова никогда не будет опровергнут!

Машину Тьюринга не пытались строить ни в натуре, ни в модели. Это не имело смысла. Она очень примитивна и крайне медлительна. Посудите сами. Для сложения 2 и 3 ей требуется 37 тактов. А для решения сколько-нибудь сложной задачи могут потребоваться миллиарды миллиардов тактов и миллионы километров ленты.

Задачу, которую человек решает за несколько часов, машина Тьюринга будет решать, может быть, тысячелетия.

Любая современная вычислительная машина, и особенно электронная, неизмеримо производительнее, чем машина Тьюринга. И такие высокопроизводительные машины человек использует в своей практической работе.

Но машина Тьюринга, существующая только на бумаге, имеет очень важное теоретическое значение. Она очень наглядно показывает, как с помощью алгоритма самый сложный процесс распадается на простые и однообразные операции. Она помогает изучать принципиальные возможности механизации умственного труда человека.

Теперь мы уже точно знаем: автоматизировать можно лишь те процессы, для которых существует схема их реализации машиной Тьюринга. А там, где она бессильна, бессильной окажется любая самая совершенная и быстроходная электронная машина не только сегодняшнего дня, но и будущего.

С алгоритмически неразрешимыми задачами способен справиться только мозг человека.