г) Пропускная способность канала

Экономичность передачи сообщения зависит от правильности кодирования его. Кодирование сигнала по существу означает сравнение символов одного алфавита с символами другого алфавита, причем код представляет собой комплекс правил такого сравнения. Коды могут иметь различные размеры: например, скульптура имеет код, заданный тремя пространственными координатами, фильм - двумя пространственными и одной временной координатой и т. д.; скульптура существует, конечно, и во времени, однако она не изменяется во времени, и неизменяющийся сигнал не несет новой информации. Эти коды можно по-разному трансформировать. Например, при фотографировании скульптуры трехразмерный код изменяется в двухразмерный, при чтении одноразмерный пространственный код букв измен во временной.

Естественно, что при кодировании может измениться количество символов и их вероятностное распределение. Например, один символ может быть отнесен к определенной комбинации символов или наоборот. При выборе кодов всегда изыскивают наиболее экономичный для данной передачи код. Какой-то код имеет наивысшую энтропию на символ, то есть наименьшее число символов, необходимых для данного количества передаваемой информации. Наиболее экономичный код требует минимального числа символов и минимального времени на передачу.

Хороший код должен сохранить все нужное в сообщении и исключить ненужное так, чтобы пространство передачи было использовано наиболее экономично в течение продолжительности передачи данного сообщения.

Ограничение в передаче обусловлено пропускной способностью канала. При формировании сообщения в сигналы необходимо добиваться экономичного использования пространства. Теория информации исследует зависимости между величиной сообщения, пространством передачи и помехами, действующими во время передачи помех. Она исследует математическими методами ограничения, имеющие место при передаче сигналов, поддающихся выражению в виде функциональной кривой, заданной взаимозависимостью частоты, амплитуды и времени. Пропускная способность канала передачи определяет, какое количество информации может быть передано за определенное время.

На пропускную способность канала влияет источник помех, под которыми понимаются изменения передаваемых сигналов, следствием которых является, например, искажение звука, отображения телеграфного сообщения и т. д. Вследствие помех количество информации в переданном сообщении всегда уменьшается при передаче и никогда не увеличивается, то есть количество принятой информации может быть лишь в идеальном случае таким же (но не больше), как и количество переданной информации. Этот идеальный случай возможен только в канале без шума. Шум вызывает искажение сообщения, рост неопределенности в передаваемом сообщении, причем этот шум может иметь своим следствием как исчезновение определенных переданных элементов сообщения, так и появление новых элементов в переданном сообщении.

Пропускная способность канала представляет собой число "независимых" "да - нет" решений, которые можно передавать в единицу времени. Ограничение канала, обусловленное его пропускной способностью, определяет подходящую статистическую структуру для передаваемых сигналов¹. Мера передачи информации по шумовому каналу задается по формуле Шеннона

¹ (Популярный пример ограниченной пропускной способности канала связи: если я хочу послать телеграмму и пропускная способность моей передачи ограничена суммой денег, которую я намерен истратить на телеграмму, то я вынужден соответственно закодировать телеграмму, то есть подобрать такие слова, которыми я могу изложить суть сообщения покороче. Пропускная способность канала может быть ограничена также особенностями приемника, то есть, например, она будет более ограничена при разговоре с ребенком, чем при разговоре со взрослым.)

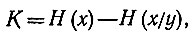
где Н (х) - энтропия входа, а Н (х/у) - условная энтропия, показывающая, что при поступлении информации y было передано х информации.

Согласно Шеннону, принятый сигнал E является функцией переданного сигнала S и шума N, следовательно,

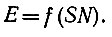
В канале без шума энтропия входа равна энтропии выхода, следовательно,

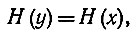
то есть принятый сигнал E является только функцией преданного сигнала S. Если канал с шумом и мы оперируем только с принятым сигналов, то вообще невозможно воспроизвести первоначальное сообщение или переданный сигнал с полной уверенностью.

Максимальная пропускная способность канала с помехой равна, по Шеннону, разности энтропии входа и условной энтропии выхода:

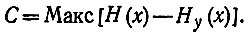
При передаче без шума условная энтропия выхода равна нулю, следовательно, пропускная способность тогда равна энтропии входа. Максимальные пропускные способности могут быть достигнуты только асимптотически: для этого нужно 'было бы выбрать оптимальный код, который, однако, требует больше времени на передачу, так как он связан с большой возможностью аварийности (с малой помехоустойчивостью).

Для иллюстрации приводим, по Шеннону, пример передачи с помехами: имеются два возможных символа 0 и 1, и мы передаем 1000 символов в секунду с вероятностью p₀ - p₁ = ^l/₂. Источник производит информацию в 1000 двоичных единиц информации в секунду. При этом шум создает такие помехи, что в среднем один из ста символов принимается неточно, то есть тогда принимается 0 вместо 1 или 1 вместо 0. Мера передачи и количество передаваемой информации будут в этом случае меньше 1000 двоичных единиц информации в секунду, здесь будет, следовательно, 990 таких единиц в секунду, причем получатель не знает, где скрыты ошибки. Крайний случай имел бы место тогда, когда помехи настолько велики, что принятые символы не зависят от переданных символов. Поскольку вероятность для поступления 1 и 0 равна ¹/₂, то в этом случае половина принятых символов принята правильно, а мера передачи будет здесь, следовательно, 500 двоичных единиц информации в секунду.

Определение пропускной способности канала, данное Шенноном, - это прежде всего статистическое определение. Мейер-Эпплер ограничивает эту пропускную способность физически¹. Согласно Мейер-Эпплеру, можно выразить информационную емкость системы следующим образом:

¹ (См. W. Meyer-Eppler, Informationstheorie, "Naturwiss.", № 15, 1952.)

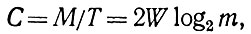
где M - мера так называемого нагрузочного пространства сообщения, то есть мера нагрузки, заполнения пространства передачи, заданная количеством информации передаваемого сообщения, Т - продолжительность передачи, W - ширина полосы частот, m - число метронов, то есть поддающихся различению энергетических ступеней. Условием передачи сигнала по каналу является то, что объем сигнала был всегда меньше пропускной способности канала. Максимально эффективное использование канала было бы возможно при равенстве объема сигнала и пропускной способности канала.

Содержание сообщения зависит от длины сигнала и поэтому оно определяется в секундах потока. Поток сообщений или поток информации задается числом решений при передаче за одну секунду и выражается как

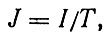
где I - содержание информации в сообщении, а Т - продолжительность передачи. Максимальный поток определяет информационную пропускную способность системы, зависящую от предельной частоты сигналов и от числа поддающихся различению степеней свободы системы (энергетических уровней, ступеней амплитуды). Если пропускная способность меньше потока, то при передаче теряется определенное количество информации. Если, наоборот, эта пропускная способность больше, то поток информации может проходить через систему хорошо. Для возмещения потерь при передаче необходимо использовать повторную или замедленную передачу. Если, например, у нас плохой телефон, то необходимо повторять сказанные слова или же уменьшить поток информации путем снижения скорости разговора или же, наконец, произносить слова особо отчетливо.

Скорость передачи указывает количество информации при расчете энтропии на единицу времени, и она равна разности безусловной и условной энтропии. При отсутствии помех условная энтропия имеет нулевое значение, а скорость переноса равна энтропии входа, то есть все переданное количество принимается получателем. Если же, наоборот, помехи настолько велики, что условная энтропия равна энтропии входа, то информация не передается и тогда скорость передачи - нулевая. Скорость передачи зависит от распределения вероятностей сообщения и помех и от статистической связи входа и выхода. При использовании правильного кода скорость передачи мало чем отличается от пропускной способности канала. И при пользовании экономичными кодами все же вероятность погрешности в канале без помех никогда не бывает нулевой. Скорость передачи зависит от влияния помех. Чем выше уровень этих помех, тем больше вероятность ошибок. Для защиты от помех применяют наряду с замедленной или повторной передачей также и так называемые самокорректирующиеся или контрольные коды. В контрольном коде добавляют к каждой группе из N символов сообщения контрольный символ, не несущий информацию сам по себе, но дающий возможность обнаружить ошибку (обнаружить, но не исправить или указать место ее). Конечно, более сложные коды 'связаны с задержкой во времени, с увеличением продолжительности передачи.

Зависимость меры пропускной способности канала от помех выражена в теореме Шеннона следующим образом:

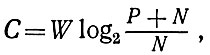
где W - ширина полосы частот, P - средняя мощность сигнала, а N - средняя мощность помех.

При передаче сообщения по каналу важно знать, насколько сигнал превышает шум. Шум представляет собой частоту появления случайных помех при передаче сигнала, а возможно и при возникновении или при фиксировании его. При действии помех стираются мелкие различия между сигналами и последние становятся неразличимыми. Уровень помех является границей отличимости отдельных сигналов. Поскольку сигнал сопровождается помехой, возможно, чтобы дискретный сигнал заменял непрерывный сигнал, то есть непрерывное сообщение можно кодировать как дискретное с определенным приближением. Дело в том, что существование помех делает возможным использование непрерывного алфавита, для которого число возможных сообщений, собственно говоря, бесконечно. Величина помех по сравнению с величиной сигнала обусловливает скорость, с которой можно передавать сигналы с минимальной аварийностью (максимальной помехоустойчивостью¹). Вопрос о передаче без помех тесно связан с проблемой так называемой избыточности сообщения. Понятие избыточности сообщения наряду с понятиями информации и энтропии является одним из наиболее интересных в философском отношении понятий теории информации.

¹ (Наиболее известным видом помех является тепловой шум, состоящий в хаотическом движении молекул (броуновском движении), при котором вероятности распределены равномерно.)