1-1. Закон больших чисел

Этот раздел математической статистики целесообразно начать с неравенства Чебышева и доказать его в несколько более общем виде, чем это принято в большинстве руководств [Л. 21, 22].

Неравенство Чебышева Пусть g(X) - неотрицательная функция случайной величины X. Тогда для любого положительного числа k>0 имеем:

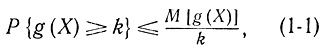
где P{g(X) ≥k} - вероятность того, что случайная величина g (X) превысит или будет равна числу k; М [g (X)] - математическое ожидание величины g (X). Для доказательства воспользуемся интегралом Лебега-Стильтьеса, который для непрерывных случайных процессов совпадает с обычным интегралом, а для дискретных - с суммой. Обо-значим через S множество всех значений X, для которых удовлетворяется неравенство g (X) ≥k. Тогда

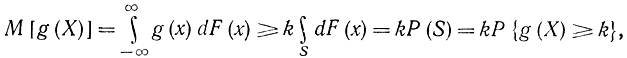
откуда и следует формула (1-1). В этом соотношении F (х) - вероятностная мера случайной величины X, совпадающая в случае непрерывной величины с плотностью распределения вероятности f(x), т. е. F (х)=f(x)dx. Функция Р(S)=Р{ g (X)≥k} равна вероятности попадания случайной величины X в множество S, которое определяется соотношением g (X) ≥k. Если величина X непрерывная и g(X)=X, то

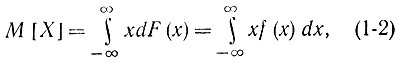
если дискретная, то

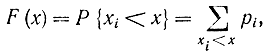
где p_i - вероятность того, что величина X примет значение x_i. Условно и здесь можно написать, что

где

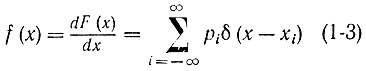
(δ(х) - дельта-функция Дирака).

Подставляя выражение (1-3) в (1-2), получаем известную формулу для математического ожидания дискретной случайной величины:

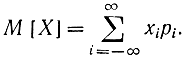
Тем самым теорема доказана для непрерывных и дискретных случайных величин.

Пример 1-1. Оценим сверху вероятность того, что скорость движения автобуса X будет лежать в пределах от 30 до 50 км/ч на участке длиной L=10 км, если математическое ожидание функции g(X)-L/|X - 40 |, зависящей от скорости, равно на этом участке М[g (X)]=0,8.

Используя формулу (1-1) и принимая k=1, получаем:

т. е. искомая вероятность не превышает 0,8.

Далее, полагая в формуле (1-1) g (X)=(X-m_x)² и k=α²σ², где m_x - математическое ожидание; σ²=D - дисперсия X; α - положительная постоянная, и учитывая, что

получаем:

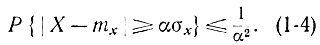
Теперь, полагая в формуле (1-4) α=α₁/σ_x и учитывая, что σ²=D_x, запишем:

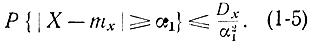
Соотношение (1-5) не что иное, как неравенство Чебышева, которое можно прочитать следующим образом: какое бы ни было положительное? число α, вероятность отклонения случайной величины X от своего математического ожидания на величину, не меньшую, чем а, не превышает D_xα².

Из неравенства Чебышева можно получить так называемое правило трех сигм. Для этого положим в формуле (1-5) α₁=3σ_x:

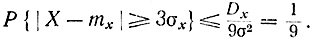
Неравенство Чебышева дает верхнюю границу: 1/9. На самом же деле часто, например в случае нормального распределения, она приблизительно составляет 0,003 (в этом можно убедиться с помощью таблиц нормального закона). Если закон распределения X неизвестен, а m_x и σ_x известны, то условно считают, что отрезок m_x±3σ_x является участком практически возможных значений. Тем самым принимают величину m_x+3σ_x за максимальное значение смещенной случайной величины (m_x≥0).

Пример 1-2. Известно, что средняя масса вылавливаемой в данной местности рыбы m_x=900 г, а дисперсия массы σ²_x=40 000 г².

Оценим сверху вероятность того, что масса выловленной рыбы будет менее 300 г, или более 1500 г, т. е. вероятность события |X-m_x|≥α. По условию задачи α=3σ_x. Согласно неравенству Чебышева

т. е. искомая вероятность не превышает 1/9≈0,1.