а) Теорема Чебышева

С помощью этой теоремы устанавливается связь между средним арифметическим конечного числа значений случайной величины и ее математическим ожиданием. Пусть имеется случайная величина X с математическим ожиданием m_x и дисперсией D_x. Произведем над ней n независимых опытов. В первом опыте X имеет значение X₁ во втором - Х₂ и т. д. Рассмотрим сумму п независимых случайных величин X_i

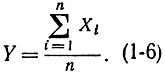
Пользуясь теоремами теории вероятности, имеем:

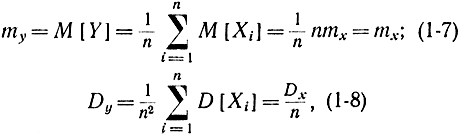
т. е. математическое ожидание среднеарифметической суммы независимых случайных величин X_i не зависит от числа опытов, а ее дисперсия убывает с их возрастанием, поэтому Y с увеличением числа опытов ведет себя как неслучайная величина и приближается к математическому ожиданию [Л. 21].

Теорема Чебышева дает точную формулировку этого явления: при достаточно большом числе независимых опытов среднее арифметическое наблюдаемых значений случайной величины сходится по вероятности к ее математическому ожиданию.

Считается, что случайная величина Х⁽ⁿ⁾ сходится по вероятности при n→∞ к величине a, если вероятность того, что Х⁽ⁿ⁾ и а сколь угодно близки, неограниченно приближается к единице при увеличении n. Математически это свойство сходимости можно записать в следующем виде:

где ε и σ - сколь угодно малые положительные числа. Если эти числа заданы, всегда можно найти такое n₀, при котором соотношение (1-9) будет удовлетворяться для любого n>n₀ Иногда эту формулу записывают как

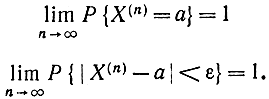
или

Теперь запишем теорему Чебышева с помощью формулы

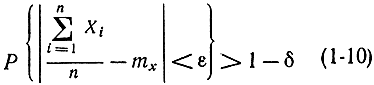
и докажем ее с помощью соотношений (1-7) и (1-8). Применяя к величине Y неравенство Чебышева для α=ε, получаем:

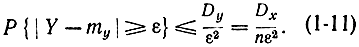
Как бы мало ни было ε, всегда можно взять n таким большим, чтобы выполнилось неравенство

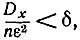
где δ - сколь угодно малое число. С помощью этого соотношения можно изменить вид формулы (1-11):

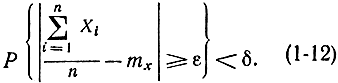
Умножим обе части этого неравенства на -1 и добавим к ним по единице, в результате

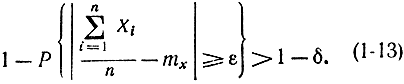
Введя противоположное событие и учитывая, что

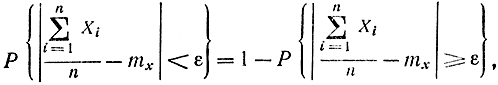
в итоге получим формулу (1-10), что и требовалось доказать.

Пример 1-3. Определим необходимое число испытаний, при котором вероятность отклонения среднего арифметического от математического ожидания на величину 0,05 и больше была бы меньше 0,01.

Используя теорему Чебышева (1-10) и вводя противоположное событие, получаем:

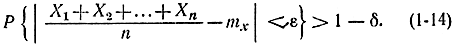
Соотношение (1-14) получается из соотношения (1-15) при условии, что

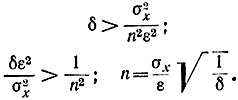
Задавшись σ_x=0,2, получим:

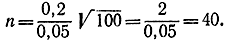
Очевидно, что для решения поставленной задачи необходимо знать дисперсию величины X, что не всегда возможно.

Существует обобщенная теорема Чебышева, в которой доказывается справедливость соотношения (1-10) для случая, когда характеристики случайной величины X изменяются от опыта к опыту. Оказывается, что и в этом случае с возрастанием числа случайных величин среднеарифметическое значение неограниченно (в вероятностном смысле) приближается к некоторой постоянной величине. По-прежнему предполагается независимость случайных величин. Точно математически теорему можно сформулировать так: если Х₁, Х₂, ..., Х_n - независимые случайные величины с математическими ожиданиями m_xi m_x2, ..., m_xn и дисперсиями D_x1, D_x2 ..., D_xn и если все дисперсии ограничены одним и тем же числом L, т. е. D_xi< L (i = 1, 2, ..., n), то при возрастании п среднеарифметическое наблюдаемых значений Х₁ Х₂, ..., Х_n сходится по вероятности к среднеарифметическому их математических ожиданий, т. е. при достаточно большом n

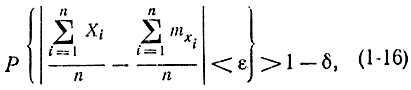
где ε и δ - сколь угодно малые числа.