б) Теорема Маркова

Результаты обобщенной теоремы Чебышева для зависимых величин можно обобщить с помощью теоремы Маркова. Если имеются зависимые случайные величины Х₁ Х₂, Х_N и если при n→∞

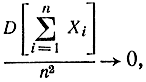
то среднеарифметическое значений случайных величин X₁ Х₂, ..., Х_n сходится по вероятности к среднеарифметическому их математических ожиданий. Для доказательства опять рассмотрим величину (1-6). Очевидно, что

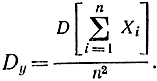
Применив к величине Y неравенство Чебышева, получим:

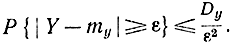
Так как при достаточно большом n величина D_y сколь угодно близка к нулю, то всегда можно выбрать такое n, при котором D_y/ε²<δ. Поэтому

или аналогично предыдущему

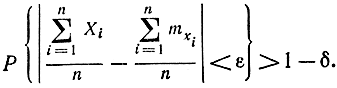
Тем самым теорема доказана.