в) Теорема Бернулли

Эта теорема устанавливает связь между частотой появления события и его вероятностью. Пусть имеется n независимых опытов и в каждом из них событие А может появиться с вероятностью р. Теорема Бернулли утверждает, что при неограниченном увеличении n частота появления А сходится по вероятности к р, т. е.

где р*=k/n - частота появления событий (k - число появления А в n опытах); ε и δ - сколь угодно малые положительные числа.

Можно дать несколько другую формулировку теоремы Бернулли: вероятность того, что частота р*=k/n отличается по модулю от своего среднего значения p не меньше чем на ε, стремится к нулю при n→∞, как бы ни было мало ε, т. е.

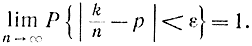
Обозначим число появлений события А в первом опыте через Х₁ во втором - через Х₂ и т. д.. Очевидно, что величины X_i могут принимать только два значения: 1 - с вероятностью р и 0 - с вероятностью q=1-р. При этом нетрудно убедиться, что

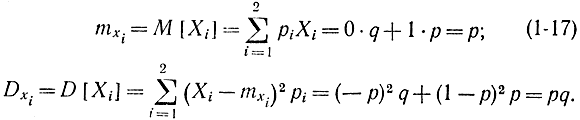
Частота р* есть не что иное, как среднее арифметическое величин X₁, X₂, ...,X_n:

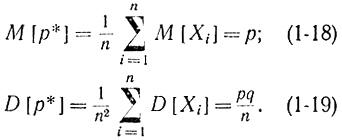
Отсюда следует, что математическое ожидание частоты р* не зависит от числа испытаний, а дисперсия стремится к нулю с их ростом. Согласно Закону больших чисел (теорема Чебышева) величина р* (аналог величины Y) сходится по вероятности к математическому ожиданию величин X_i. А это значит в соответствии с формулами (1-17) и (1-18), что величина р* сходится к своему математическому ожиданию, так как

Дадим некоторые пояснения к доказанному положению. Для этого рассмотрим свойства функции Ф(р)=р(1-р}-pq. Покажем, что она удовлетворяет соотношению:

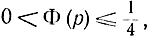
т. е.

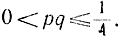
Действительно, при р=0 функция Ф(р)=0, так как Ф(р)=pq=p-p²=p(1-p); при р=1 функция Ф(р)=0; при р=1/2 функция Ф(р) достигает максимума, равного 1/4 (рис. 1-1).

Отсюда величина |р*-р| в среднем имеет порядок не ниже, чем n^-1/2. Действительно, так как pq≤1/4, то формулу (1-19) можно переписать в следующем виде:

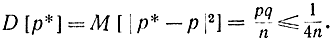
Из этого соотношения следует, что случайная величина |р*-р|² в среднем имеет порядок не более чем 1/n, а величина |р*-р| - не более чем n^-1/2. Это значит, что те значения |р*-р|, которые велики по сравнению с n^-1/2, имеют все вместе исчезающе малую вероятность. С ростом числа опытов n^-1/2 стремится к нулю и р* приближается к р.

Теорема Бернулли устанавливает устойчивость частоты появления события при неизменных условиях опыта, т. е. вероятность появления события в i-м опыте равна р независимо от i.

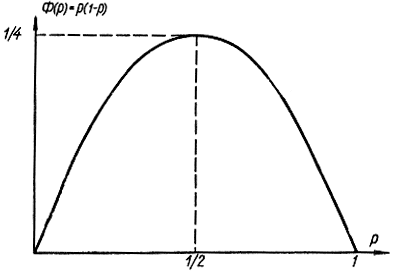
Рис. 1-1. Графика зависимости функции Ф(p)=p(1-p)

В случае изменения вероятности от опыта к опыту справедлива теорема Пуассона, которая формулируется следующим образом: если произвести n независимых опытов при вероятности появления события А в i-м опыте, равной p то с увеличением n частота р* события А сходится по вероятности к среднеарифметическому вероятностей p_i.

Теорема Пуассона имеет большое практическое значение, так как трудно соблюсти одни и те же условия при постановке опыта. Ее доказывают , аналогично предыдущему с помощью обобщенной теоремы Чебышева [Л. 21, 23].