а) Центральная предельная теорема для одинаково распределенных случайных величин

Дадим формулировку этой теоремы: если Х₁, Х₂, ..., Х_n - независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием m_x и дисперсией σ², то при неограниченном увеличении n закон распределения суммы

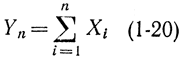
неограниченно приближается к нормальному с математическим ожиданием nm_x и дисперсией nσ².

Доказательство этой теоремы основано на понятии характеристической функции. По условию величины X_i имеют одинаковую плотность распределения вероятностей f(х). Если они непрерывные, то f(х) непрерывна, если дискретные, то f(х) состоит из дельта-функций.

Характеристическая функция определяется как обратное преобразование Фурье от функции f(x):

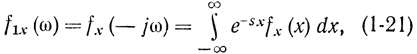
или с использованием двустороннего преобразования Лапласа, которое для функции f(х) определяется по формуле

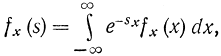
имеем:

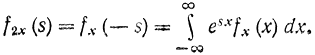
Если величины дискретные, то интеграл превращается в сумму

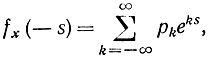
где p_k - вероятность того, что X примет какое-то k-e дискретное значение.

Так как все величины X₁, Х₂, ..., Х_n статистически независимы, то к их сумме Y_n=Х₁+Х₂+...+Х_n применима теорема о композиции [Л. 13, 15]. Плотность распределения вероятностей суммы таких величин равна кратному интегралу свертки от f_x(х), а характеристические функции перемножаются, т. е.

Одно из замечательных свойств нормального закона распределения заключается в том, что плотность распределения вероятности f(х) и характеристическая функция f₁(ω) имеют один и тот же вид:

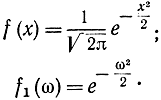
Случайная величина Y_n в соответствии с формулами (1-7) и (1-8) имеет следующие математическое ожидание и дисперсию:

Если вместо Y_n рассматривать величину с единичной дисперсией Z_n=Y_n/σn^1/2, то соответствующие характеристические функции будут связаны соотношением

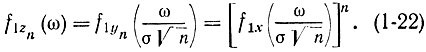
В этом нетрудно убедится с помощью формулы (1-21). Для доказательства теоремы достаточно показать, что функция

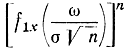
стремится к ехр(- ω²/2) при n→∞. Для этого разложим функцию f_1x(ω) в ряд Тейлора:

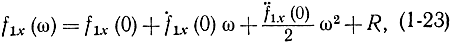
где R - остаточный член порядка малости выше, чем ω². Найдем коэффициенты этого ряда:

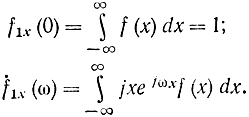
Отсюда

Положим m_x=0. При этом не нарушается общность доказательства, так как всегда можно так изменить начало координат, чтобы m_x=0:

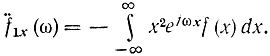
Отсюда

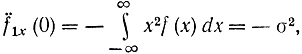
так как m_x=0. Поэтому ряд (1-23) запишется в виде

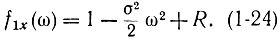
Перейдем от Y_n к нормированной величине 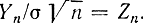. При этом в соответствии с формулой (1-22) характеристические функции будут связаны соотношением

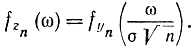
Заменив переменные в выражении (1-24), получим:

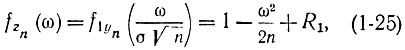
где R₁ стремится к нулю быстрее, чем 1/n.

Далее, возьмем натуральный логарифм от обеих частей равенства (1-25). Учитывая, что величина

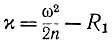
малая и стремится к нулю при n→∞ и что при этом справедливо соотношение

получаем:

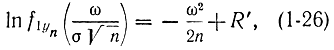
где R' - остаточный член, который стремится к нулю быстрее, чем 1/n. Умножая обе части (1-26) на n и учитывая (1-22), получаем:

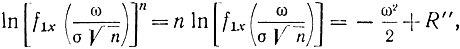
поэтому

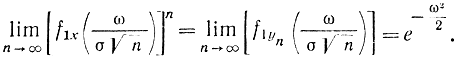
Функция, стоящая справа, - это характеристическая функция нормального распределения с m=0 и σ=1. Тем самым теорема доказана.

Аналогичным образом ЦПТ можно доказать для дискретных случайных величин.

Приведенные рассуждения основаны на том, что при стремлении последовательности характеристических функций к предельной характеристической функции соответствующая последовательность функций распределения тоже стремится к функции распределения, соответствующей этой предельной характеристической функции. Это положение может быть доказано и носит название теоремы Крамера [Л. 22].

Для общего случая, когда случайные величины независимы и имеют разные законы распределения, эту теорему можно доказать по методу А. М. Ляпунова. При этом необходимо, чтобы выполнялись условия

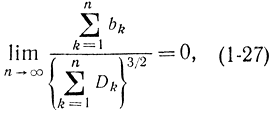
где b_k= М{|Х⁰_k|³} - третий абсолютный центральный момент величины X_k, Х⁰_k=X_k - m_k, k=1,2, ..., n; D_k - дисперсия величин X_k.

Более общим необходимым и достаточным условием справедливости ЦПТ является условие Линдеберга: при любом τ>0

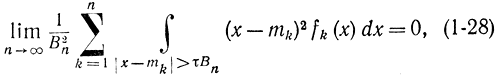
где m_k - математическое ожидание ; f_k(х) - плотность распределения случайной величины Х_k;

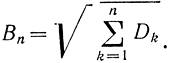
Оба условия (1-27) и (1-28) выражают одно и то же требование равноправия случайных величин в сумме. Например, если в сумме существенно выделяется Х₃, то, очевидно, что

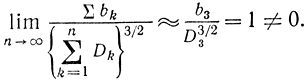
Если все X_k малые, то в числителе этого выражения стоят слагаемые с разными знаками и малые, в знаменателе - сумма положительных малых величин и при n→∞ отношение стремится к нулю.

Пример 1-4. Проиллюстрируем справедливость ЦПТ. Покажем, что сумма независимых случайных величин, распределенных по равномерному закону, стремится к нормально распределенной случайной величине [Л. 24]. Пусть случайные величины все распределены одинаково:

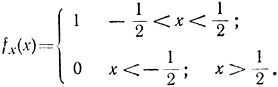
Обозначим через f_yn(y) плотность вероятностей для величины Y_n=Х₁ + Х₂ + ... + Х_n. Тогда, используя теорему о композиции независимых случайных величин, получим:

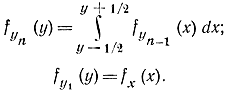
С помощью этих формул нетрудно установить, что

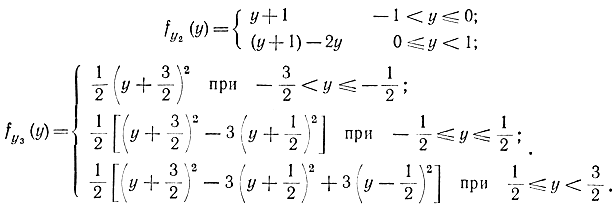
Графики функций f_y1(y), f_y2(у), f_y3(у), f_y4(у) показаны на рис. 1-2. Кривая, представленная на рис. 1-2, в, состоит из трех парабол второго порядка и достаточно близка к нормальной. Кривая рис. 1-2, г практически уже не отличается от гауссовой. Таким образом, уже при четырех слагаемых закон распределения практически совпадает с нормальным. Обычно считают, что при сумме независимых случайных величин, содержащей более 10 слагаемых, наступает нормальный закон.

Центральная предельная теорема существенно упрощает расчет характеристик случайных величин. Рассмотрим несколько случаев.

Пусть имеется n случайных величин X₁, Х₂, ..., Х_n с математическими ожиданиями m₁, m₂, ..., m_nи дисперсиями D₁, D₂, ..., D_n, выполняются условия ЦПТ и величина Y_n=∑X_i считается распределенной по нормальному закону. Тогда вероятность Y попасть в интервал [α,β] можно определить с помощью таблиц нормальной функции распределения (см. приложение 1)

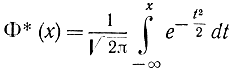
по формуле

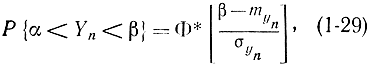
где

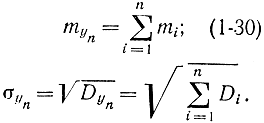
В этом случае не требуется знать закон распределения каждого слагаемого, достаточно знать их математические ожидания и дисперсии.

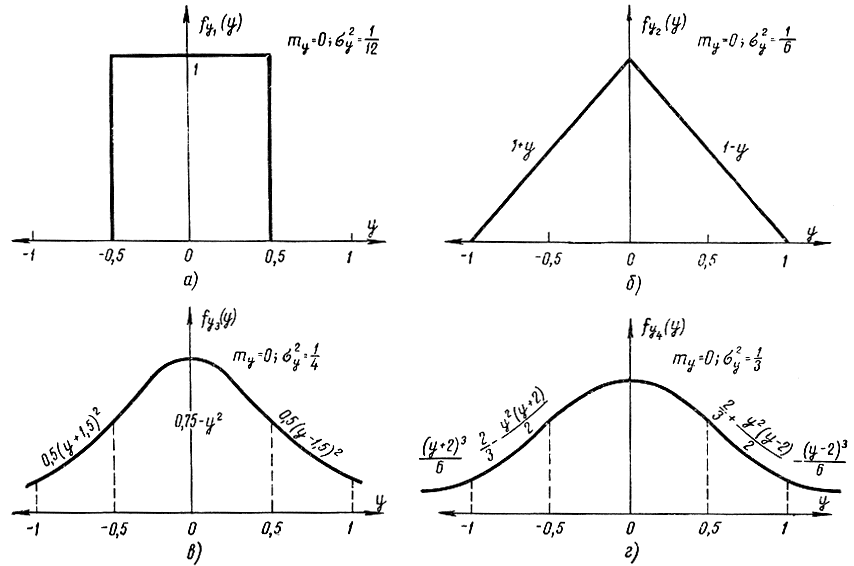
Рис. 1-2. Нормализация случайных величин при сложении

Иногда формулу (1-29) удобнее записать относительно нормированной случайной величины

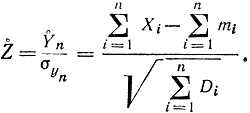
Очевидно, что m_z⁰=0 и σ_z⁰=1, поэтому