б) Теорема Муавра - Лапласа
Частным случаем ЦПТ для дискретных случайных величин является теорема Муавра - Лапласа: если производится n независимых опытов, в каждом из которых событие А появляется с вероятностью р, то справедливо соотношение
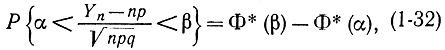
где Yn - число появления события А в n опытах; q=1-р; α и β - некоторые положительные числа.
Для доказательства (1-32) представим Yn в виде суммы (1-20), где Xi - число появлений события А в i-м опыте, причем Xi может принимать только одно из двух значений: 0 или 1. Согласно ЦПТ закон распределения этой суммы стремится к нормальному. Следовательно, величина
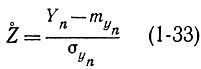
подчиняется закону распределения, близкому к нормальному, причем в данном случае
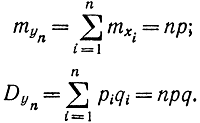
Поэтому формулу (1-33) можно переписать в виде
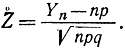
Подставим это выражение в формулу (1-31) и получим необходимое соотношение (1-32). Тем самым теорема доказана.
Пример 1-5. В соревнованиях по стрельбе участвуют 6 спортсменов. Каждый должен выстрелить по 15 мишеням. Считается, что выстрелы одного и разных спортсменов независимы. Вероятность попадания в мишень равна 0,4. Найдем вероятность р того, что из 90 мишеней не менее 35% будут поражены.
Обозначим через 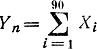 общее число пораженных мишеней, где Xi - число мишеней, пораженных при i-м выстреле (i= 1, 2, 90). Очевидно, что для Xi вероятности соответственно равны:
общее число пораженных мишеней, где Xi - число мишеней, пораженных при i-м выстреле (i= 1, 2, 90). Очевидно, что для Xi вероятности соответственно равны:
P{Xi=0}=0,6=q
Р{Хi=1}=0,4=р.
Отсюда
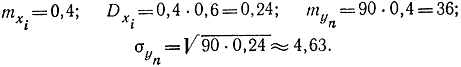
Применим формулу Муавра - Лапласа (1-32) или, точнее (1-30), в результате получим:
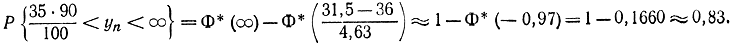
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'