Глава вторая. Теория оценок

Теория оценок - классический раздел математической статистики. Суть ее - в определении числовых значений характеристик случайных величин на основании ограниченного числа испытаний.

Теория оценок имеет дело с числовыми оценками, а не с определением законов распределения, этим вопросом занимается другой раздел математической статистики, называемый проверкой статистических гипотез [Л. 21, 25].

Очевидно, что любое числовое значение характеристики случайной величины, вычисленное на основании ограниченного числа испытаний, будет случайной величиной. Это значение носит название оценки параметра. Так, среднее арифметическое результатов конечного числа испытаний представляет собой оценку математического ожидания и является величиной случайной. Чем больше число испытаний, тем меньше ошибка в оценке. Теория оценок исследует методы получения более точных оценок параметров случайной величины при заданном числе испытаний. Она определяет, сколько необходимо сделать испытаний, чтобы обеспечить заданную точность оценки параметра. Если имеется n испытаний случайной величины X и наблюденные значения этой величины Х₁, Х₂, .... Х_n, то оценка ã параметра а будет функцией Х₁, Х₂, .... Х_n:

Закон распределения а зависит от закона распределения X и числа опытов. Оценка должна удовлетворять некоторым общим требованиям.

Прежде всего она должна быть состоятельной, т. е. с увеличением числа испытаний ã должна сходиться по вероятности к а.

Оценка должна быть несмещенной, т. е. она не должна содержать систематических (в среднем) отклонений:

Наконец, оценка должна быть эффективной, т. е. в среднем иметь минимальный разброс

Иногда для определения эффективности оценки выбирают функцию максимального правдоподобия: а считается эффективной или оптимальной, если условная вероятность имеет максимальное значение. Допустим, требуется дать оценку математического ожидания m _x при условии, что

Перебирая все возможные виды оценок ã, следует остановиться на той, которая дает этой функции максимум. В этом смысл критерия максимального правдоподобия. Если опыты независимы и случайная величина подчинена нормальному закону, то можно показать, что эффективная (в смысле приведенных двух критериев) оценка для математического ожидания будет при

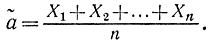
Возможны и другие критерии эффективности (байесовский, минимаксный).

На практике не всегда удается удовлетворить всем этим требованиям одновременно. В зависимости от задачи конструктор выбирает критерий эффективности.

Теория оценок тесно связана с теорией статистических решений, так как выбор оценки существенно зависит от той задачи, в которой необходимо принимать решение.

Имеется еще одно общее понятие теории оценок - достаточность статистики: если наблюденных результатов Х₁, Х₂, ..., Х_n достаточно для получения всех оценок величины X, то статистика называется достаточной.

Различают два вида оценок: точечные и интервальные.

В первом случае интересуются одним значением (точкой), во втором - интервалом значений, т. е. при интервальных оценках стараются определить вероятность того, что отклонение оценки параметра от истинного значения будет не меньше заданной величины. Для определения близости оценки к оцениваемому параметру вводят доверительный интервал близости ε, а саму близость оценивают по величине вероятности р, которую называют доверительной вероятностью β, и задают заранее р=β. Таким образом, задача оценки состоит в том, чтобы выбрать или произвести такое число опытов, при котором

Здесь интервал (а-ε, а+ε) - доверительный.